LeetCode259~282题解

LeetCode260.只出现一次的数字Ⅲ：

题目描述：

给你一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。

你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。

示例 1：

输入：nums = [1,2,1,3,2,5]
输出：[3,5]
解释：[5, 3] 也是有效的答案。

示例 2：

输入：nums = [-1,0]
输出：[-1,0]

示例 3：

输入：nums = [0,1]
输出：[1,0]

提示：

2 <= nums.length <= 3 * 10^4
-2^31 <= nums[i] <= 2^31 - 1
除两个只出现一次的整数外，nums 中的其他数字都出现两次

思路：

由前面的只有一个不同的数字为前提，通过全部异或将其他出现两次的数消去，最后剩下的就是出现一次的数。

这里利用两次思想： 先将所有数异或起来，最终得到的结果为a^b,那么对于该结果来说a和b肯定是至少存在某一位上的二进制表示不一致，例如：第k位， a为0， b为1,那么我们我们可以通过将所有第k位为0的划分到一起（包含a）：那么在这些数当中除了a，其他都是两两成对出现，那么我们再将该类异或一下，就可以得到a，同理那么我们我们可以通过将所有第k位为1的划分到一起（包含b）：那么在这些数当中除了b，其他都是两两成对出现，那么我们再将该类异或一下，就可以得到b。

时间复杂度：仅遍历两次数字，时间复杂度为O(n)

注释代码：

class Solution {
public:int get(vector<int>& nums, int k, int t){int res = 0;for(auto x : nums){if((x >> k & 1) == t) //将每个元素的第k位为t的数异或起来{res ^= x;}}return res;}vector<int> singleNumber(vector<int>& nums) {int ab = 0;for(auto x : nums) ab ^= x;//找到ab第一个为0的位数：也就是只出现一次的数异或不同的第一位int k = 0;while((ab >> k & 1) == 0) k++; return {get(nums, k, 0), get(nums, k, 1)};}
};

纯享版：

class Solution {
public:int get(vector<int>& nums, int k, int t){int res = 0;for(auto x : nums){if((x >> k & 1) == t) res ^= x;}return res;}vector<int> singleNumber(vector<int>& nums) {int ab = 0;for(auto x : nums) ab ^= x;int k = 0;while((ab >> k & 1) == 0) k++;return {get(nums, k, 0), get(nums, k, 1)};}
};

---

LeetCode263.丑数：

题目描述：

丑数 就是只包含质因数 2、3 和 5 的 正 整数。

给你一个整数 n ，请你判断 n 是否为 丑数 。如果是，返回 true ；否则，返回 false 。

示例 1：

输入：n = 6
输出：true
解释：6 = 2 × 3
示例 2：

输入：n = 1
输出：true
解释：1 没有质因数。
示例 3：

输入：n = 14
输出：false
解释：14 不是丑数，因为它包含了另外一个质因数 7 。

提示：

-2^31 <= n <= 2^31 - 1

思路：

反向思路：将n中的所有2，3，5质因子全部除干净之后，判断n是否为1，如果不是则说明原本的n不是丑数，反之则是丑数。

时间复杂度：

代码：

class Solution {
public:bool isUgly(int n) {if(n < 1) return false;while(n % 2 == 0) n /= 2;while(n % 3 == 0) n /= 3;while(n % 5 == 0) n /= 5;return n == 1;}
};

---

LeetCode264.丑数Ⅱ：

题目描述：

给你一个整数 n ，请你找出并返回第 n 个 丑数 。

丑数 就是质因子只包含 2、3 和 5 的正整数。

示例 1：

输入：n = 10
输出：12
解释：[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。

示例 2：

输入：n = 1
输出：1
解释：1 通常被视为丑数。

提示：

1 <= n <= 1690

思路：

题目需要求出丑数序列，我们根据丑数定义，丑数分为四个集合：
1.1是特例
2.质因子2的集合S2： 12，22，32，42…
3.质因子3的集合S3： 13，23，33，43…
4.质因子5的集合S5： 15，25，35，45，5*5…
对于所有丑数的集合来说，它就是由上面四个集合的并集组合而成，由于上述集合都是有序的，所以这里可以使用归并排序来使得最终的集合是有序的，也就是使用三个指针分别对2，3，4中的集合进行排序，每次将最小的丑数位置上的指针往后移动一位，如果有相同的则将相同的指针均移动一位。

现在就是如何将三个集合得到，那么我们可以发现，将质因子2的集合中的丑数全部提取出2之后，集合中的数一定还都是丑数，那么我们发现提取完质因子2之后集合的本质就是最终的丑数集合S2=S*2，同理可得S3=S*3, S5=S*5。所以三个集合都可以由S构造出来，那么我们可以在获得S的同时构造出三个集合，并且由三个集合获得S。

时间复杂度： O(n)

注释代码：

class Solution {
public:int nthUglyNumber(int n) {vector<int> q(1, 1);  //开一个初始化长度为1，且每个元素值为1的数组，用于从前往后有序存储丑数//i， j， k三 个指针从第0个元素开始，当q的元素长度达到n则证明最后一个元素是需要的第n个丑数for(int i = 0, j = 0, k = 0; q.size() < n;){//判断出i，j，k三个指针中属于每个质因子的丑数，找出其中最小的int t = min(q[i] * 2, min(q[j] * 3, q[k] * 5));//如果三个指针所属的丑数集合等于当前最小的丑数，那么对应指针往后移动一位if(q[i] * 2 == t) i++;if(q[j] * 3 == t) j++;if(q[k] * 5 == t) k++;q.push_back(t);  //将当前最小丑数有序添加到数组中}return q.back();//q的最后一位就是第n位丑数}
};

纯享版：

class Solution {
public:int nthUglyNumber(int n) {vector<int> q(1, 1);for(int i = 0, j = 0, k = 0; q.size() < n; ){int t = min(q[i] *2, min(q[j] * 3, q[k] * 5));if(q[i] * 2 == t) i++;if(q[j] * 3 == t) j++;if(q[k] * 5 == t) k++;q.push_back(t);}return q.back();}
};

---

LeetCode268.缺失数字：

题目描述：

给定一个包含 [0, n] 中 n 个数的数组 nums ，找出 [0, n] 这个范围内没有出现在数组中的那个数。

示例 1：

输入：nums = [3,0,1]

输出：2

解释：n = 3，因为有 3 个数字，所以所有的数字都在范围 [0,3] 内。2 是丢失的数字，因为它没有出现在 nums 中。

示例 2：

输入：nums = [0,1]

输出：2

解释：n = 2，因为有 2 个数字，所以所有的数字都在范围 [0,2] 内。2 是丢失的数字，因为它没有出现在 nums 中。

示例 3：

输入：nums = [9,6,4,2,3,5,7,0,1]

输出：8

解释：n = 9，因为有 9 个数字，所以所有的数字都在范围 [0,9] 内。8 是丢失的数字，因为它没有出现在 nums 中。

提示：

n == nums.length
1 <= n <= 10^4
0 <= nums[i] <= n
nums 中的所有数字都 独一无二

进阶：你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题?

思路：

题意：给出一个包含n个数的数组，要求找到0~n中缺失的数字

对0~n进行求和就是前n项和求和公式，那么只需要减去数组中的每一项元素，剩下的就是缺失的数字。

时间复杂度： O(n) ，空间复杂度：O(1)

代码：

class Solution {
public:int missingNumber(vector<int>& nums) {int n = nums.size();int s = n * (n + 1) / 2;for(auto num : nums){s = s - num;}return s;}
};

---

LeetCode273.整数转换英文表示：

题目描述：

将非负整数 num 转换为其对应的英文表示。

示例 1：

输入：num = 123
输出：“One Hundred Twenty Three”

示例 2：

输入：num = 12345
输出：“Twelve Thousand Three Hundred Forty Five”

示例 3：

输入：num = 1234567
输出：“One Million Two Hundred Thirty Four Thousand Five Hundred Sixty Seven”

提示：

0 <= num <= 2^31 - 1

思路：

题意：根据给定的数字表示，求出对应的英文表达

做法：英文中它是三位作为一个进位的，比如 thousand， million，billion，如果一个个数字去单独对应肯定很繁琐，那么我们需要分段结合规律进行叠加，比如每三位可以看成是1~999的单独阶段，将每个阶段的表达式求出来，最后加上每个阶段的描述符组合在一起就是最终的形式。
同时需要注意的是，英文的表达0_19，20_90的表示各有千秋， 所以我们需要单独开数组将特定的表达存在数组中，最后在求表达式时通过映射到下标找到对应的表示。

时间复杂度：O(n)

注释代码：

class Solution {
public:string num0_19[20] = {"Zero","One","Two","Three","Four","Five","Six","Seven","Eight","Nine","Ten","Eleven","Twelve","Thirteen","Fourteen","Fifteen","Sixteen","Seventeen","Eighteen","Nineteen",};string num20_90[8] = {"Twenty","Thirty","Forty","Fifty","Sixty","Seventy","Eighty","Ninety",};string num1000[4] = {"Billion ","Million ","Thousand ","",};string get(int x)  //返回1 ~999的英文表示{string res;if(x >= 100){//如果x大于100，说明有百位的，找到属于百位的数字的字符串表达，同时加上百位描述符res += num0_19[x / 100] + " Hundred ";x %= 100;  //将x百位抹去}if(x >= 20){//如果大于等于20，说明当前位是十位的规范表达，找到对应的字符串表达res += num20_90[x / 10 - 2] + " ";x %= 10; //除去当前十位if(x) res += num0_19[x] + ' ';  //十位剩下的则找到对应个位字符串表达}else if(x) res += num0_19[x] + ' ';  //根据x找到对应0~19的英文表达return res;}string numberToWords(int num) {string res;if(!num) return "Zero";for(int i = 1e9, j = 0; i >= 1; i /= 1000, j++) //从1billion开始，每次i减少1000，也就是三位算一次{if(num >= i) //如果当前num是大于等于该阶段，则将该阶段的数字拿出来，获取表达，并加上阶段对应的描述符{res += get(num / i) + num1000[j];}num %= i;  //将表示过的阶段去除，进入下一阶段}res.pop_back(); //最后有多余空格return res;}
};

纯享版：

class Solution {
public:string num0_19[20] = {"Zero","One","Two","Three","Four","Five","Six","Seven","Eight","Nine","Ten","Eleven","Twelve","Thirteen","Fourteen","Fifteen","Sixteen","Seventeen","Eighteen","Nineteen",};string num20_90[8] = {"Twenty","Thirty","Forty","Fifty","Sixty","Seventy","Eighty","Ninety",};string num1000[4] = {"Billion ","Million ", "Thousand ","",};string get(int x){string res;if(x >= 100){res += num0_19[x / 100] + " Hundred ";x %= 100;}if(x >= 20){res += num20_90[x / 10 - 2] + ' ';x %= 10;if(x) res += num0_19[x] + ' ';}else if(x) res += num0_19[x] + ' ';return res;}string numberToWords(int num) {if(!num) return "Zero";string res;for(int i = 1e9, j = 0; i >= 1; i /= 1000, j++){if(num >= i){res += get(num / i) + num1000[j];num %= i;}}res.pop_back();return res;}
};

---

LeetCode274.H指数：

题目描述：

给你一个整数数组 citations ，其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。

根据维基百科上 h 指数的定义：h 代表“高引用次数” ，一名科研人员的 h 指数 是指他（她）至少发表了 h 篇论文，并且 至少 有 h 篇论文被引用次数大于等于 h 。如果 h 有多种可能的值，h 指数 是其中最大的那个。

示例 1：

输入：citations = [3,0,6,1,5]
输出：3
解释：给定数组表示研究者总共有 5 篇论文，每篇论文相应的被引用了 3, 0, 6, 1, 5 次。
由于研究者有 3 篇论文每篇 至少 被引用了 3 次，其余两篇论文每篇被引用 不多于 3 次，所以她的 h 指数是 3。

示例 2：

输入：citations = [1,3,1]
输出：1

提示：

n == citations.length
1 <= n <= 5000
0 <= citations[i] <= 1000

思路：

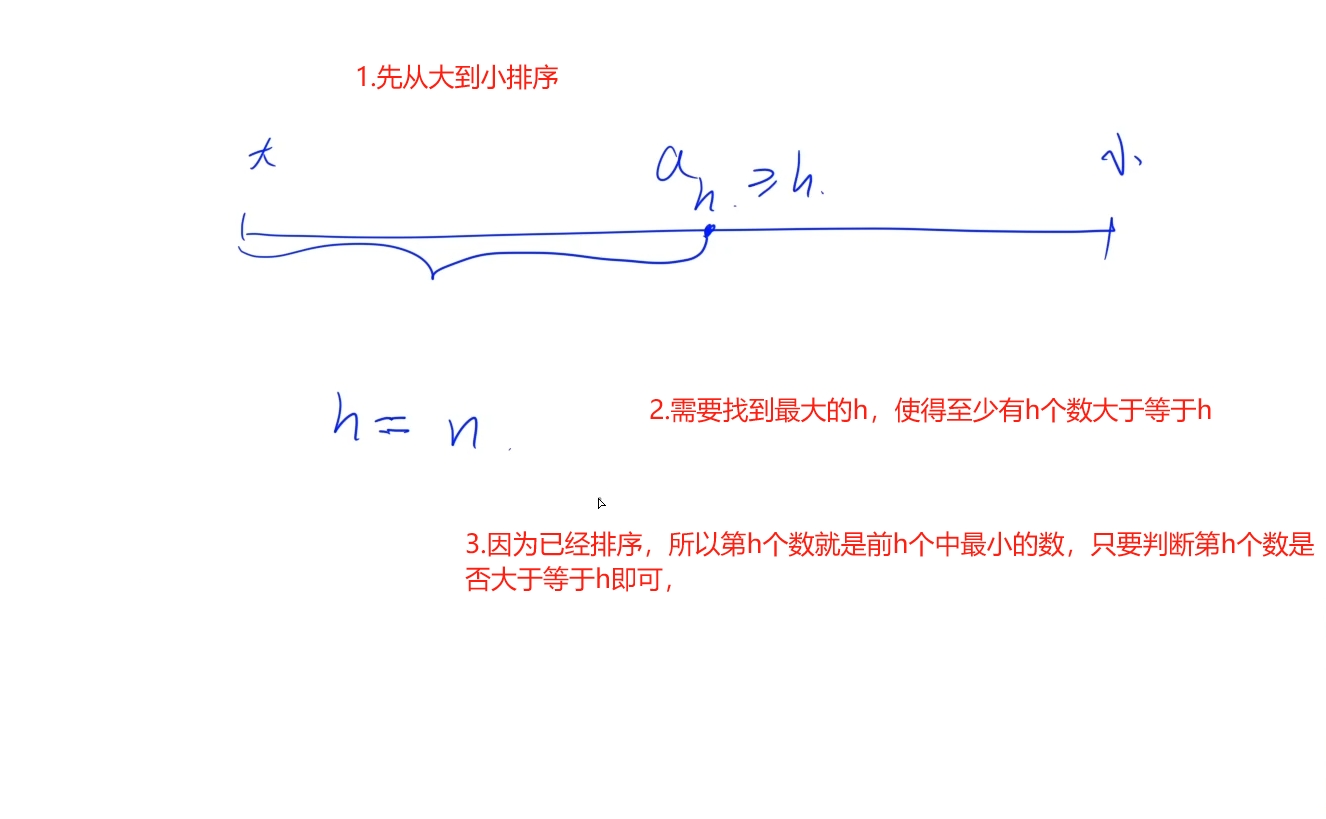
时间复杂度：O(nlogn)

代码：

class Solution {
public:int hIndex(vector<int>& c) {sort(c.begin(), c.end(), greater<int>());for(int h = c.size() ; h >= 1; h--){if(c[h - 1] >= h) return h;}return 0;}
};

---

LeetCode275.H指数Ⅱ：

题目描述：

给你一个整数数组 citations ，其中 citations[i] 表示研究者的第 i 篇论文被引用的次数，citations 已经按照 升序排列 。计算并返回该研究者的 h 指数。

h 指数的定义：h 代表“高引用次数”（high citations），一名科研人员的 h 指数是指他（她）的 （n 篇论文中）至少 有 h 篇论文分别被引用了至少 h 次。

请你设计并实现对数时间复杂度的算法解决此问题。

示例 1：

输入：citations = [0,1,3,5,6]
输出：3
解释：给定数组表示研究者总共有 5 篇论文，每篇论文相应的被引用了 0, 1, 3, 5, 6 次。
由于研究者有3篇论文每篇 至少 被引用了 3 次，其余两篇论文每篇被引用 不多于 3 次，所以她的 h 指数是 3 。

示例 2：

输入：citations = [1,2,100]
输出：2

提示：

n == citations.length
1 <= n <= 10^5
0 <= citations[i] <= 1000
citations 按 升序排列

思路：

由于已经从小到大排序好了，为了优化时间复杂度，不能直接将整个数组翻转，那么我们为了优化时间复杂度，寻找单调性：

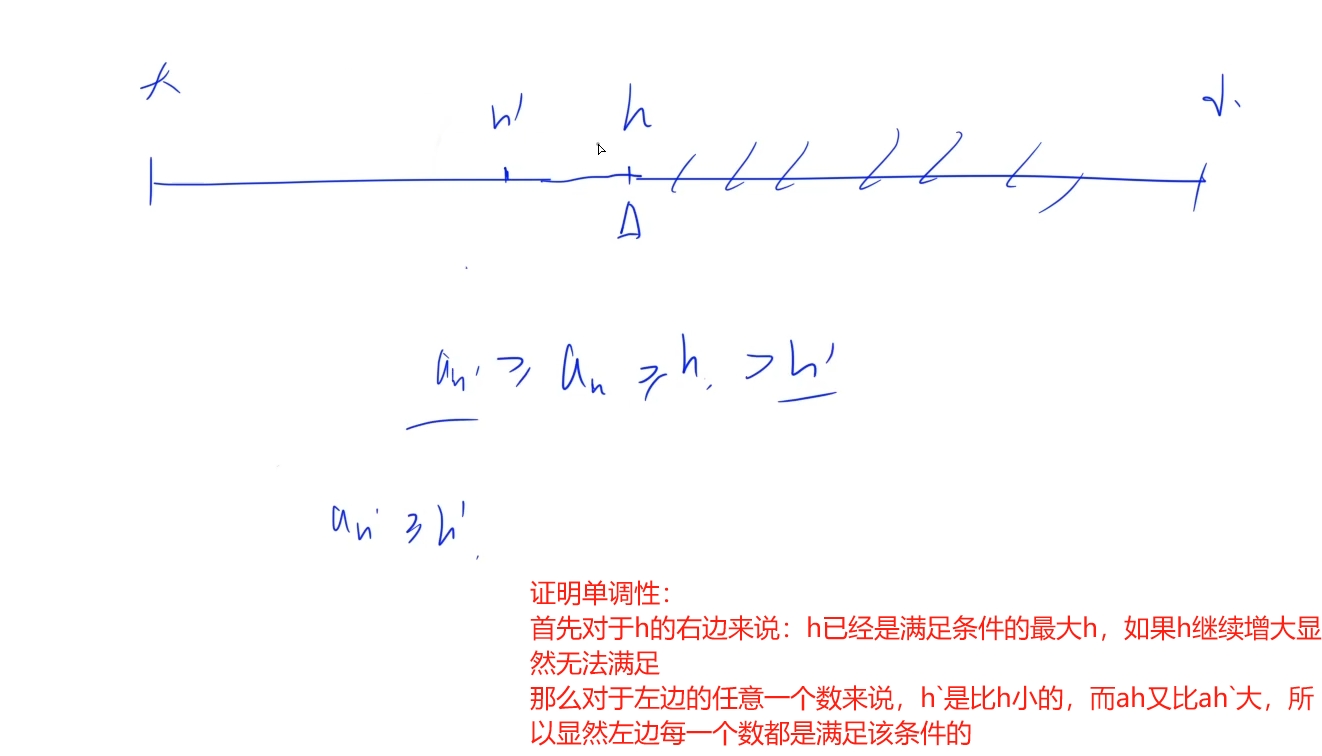
有了单调性则可以使用二分进行分段找到边界。

时间复杂度：O(logn)

代码：

class Solution {
public:int hIndex(vector<int>& c) {int n = c.size();int l = 0, r = n;while(l < r){int mid = l + r + 1 >> 1;if(c[n - mid] >= mid) l = mid;else r = mid - 1;}return r;}
};

---

LeetCode278.第一个错误的版本：

题目描述：

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, …, n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

示例 1：

输入：n = 5, bad = 4
输出：4
解释：
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以，4 是第一个错误的版本。

示例 2：

输入：n = 1, bad = 1
输出：1

提示：

1 <= bad <= n <= 2^31 - 1

思路：

题意：从1到n中，存在一个开始错误的版本导致后面的版本全部错误，也就是从bad之后的全部数都是bad状态

可以容易判断，从1~n的区间有明显的二段性，所以，可以使用二分进行边界的确定。

时间复杂度：O(logn)

代码：

// The API isBadVersion is defined for you.
// bool isBadVersion(int version);class Solution {
public:int firstBadVersion(int n) {int l = 1, r = n;while(l < r){int mid = (long long)l + r >> 1;  //可能溢出if(isBadVersion(mid)) r = mid;else l = mid + 1;}return r;}
};

---

LeetCode279.完全平方数：

题目描述：

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入：n = 12
输出：3
解释：12 = 4 + 4 + 4

示例 2：

输入：n = 13
输出：2
解释：13 = 4 + 9

提示：

1 <= n <= 10^4

思路：

题意：给出一个n，需要确定最少需要多少个平方数刚好组成n

根据数学定理：

1.四方定理：所有自然数至多只要用四个数的平方和就可以表示
2.当且仅当n != 4^a(8b + 7) 则n恰好可以由三个平方数组成
3.a^2 + b^2 = n:可以判断n是否由两个平方数组成
4.sqrt(n) * sqrt(n) = n则说明n本身是平方数

时间复杂度：O(根号n)

代码：

class Solution {
public:bool check(int x)  //求x是否是由一个(也就是本身)数平方而成的{int r = sqrt(x);return r * r == x;}int numSquares(int n) {if(check(n)) return 1;  //如果n本身是平方数则只需要一个for(int a = 1; a <= n / a; a++)  //a^2 + b^2 = n{if(check(n - a * a)) return 2;}//n != 4^a(8b + 7) 则说明n可以恰好由3个平方数组成while(n % 4 == 0) n /= 4;  if(n % 8 != 7) return 3;  return 4;}
};