当前位置： 首页 > ds >正文

C/C++ 数据结构 —— 线索二叉树

ds 2025/8/28 12:22:58

在这里插入图片描述

在这里插入图片描述

🎁个人主页：工藤新一¹

​ 🔍系列专栏：C++面向对象（类和对象篇）

​ 🌟心中的天空之城，终会照亮我前方的路

​ 🎉欢迎大家点赞👍评论📝收藏⭐文章

文章目录

  • 线索二叉树
    • 一、基本概念
        • 🎯 核心思想：变废为宝
    • 二、为什么需要线索二叉树？
        • 📊 普通二叉树的问题
    • 三、线索化规则
        • 📝 节点结构定义
    • 四、线索化二叉树
      • 4.1前序遍历
          • ⚡ 核心优势：高效遍历
        • 4.1.1前序遍历线索化二叉树思路
          • 🎨 直观理解
        • 4.1.2🔄前序遍历线索化二叉树实现
      • 4.2中序遍历
        • 4.2.1中序遍历线索化二叉树思路
        • 4.2.2🔄中序遍历线索化二叉树实现
      • 4.3后序遍历
    • 五、小结
          • 📈 ✅性能对比
          • 🎯 适用场景

线索二叉树

🎯 📊 🔧 📝🎨 🛠️⚡ 📈🎯💡

一、基本概念

🎯 核心思想：变废为宝

普通二叉树中有大量空指针域（“线索二叉树是对普通二叉树的改进”），线索二叉树 利用这些空指针域来存储遍历顺序的前驱和后继信息，从而实现对二叉树的高效遍历

二、为什么需要线索二叉树？

📊 普通二叉树的问题

在普通二叉树中：

C++typedef struct TreeNode{int val;struct TreeNode* left;struct TreeNode* right;}TreeNode;

问题：

  • 空指针浪费：约有 50% 的指针域为空（n个节点有2n个指针，实际只用n-1个）

  • 遍历效率低：需要**递归或栈[循环遍历]**，空间复杂度高

三、线索化规则

解决方案：根据遍历策略进行相应的线索化

为每个节点增加两个标志位：

  • ltag：0表示left指向左孩子，1表示left指向前驱
  • rtag：0表示right指向右孩子，1表示right指向后继

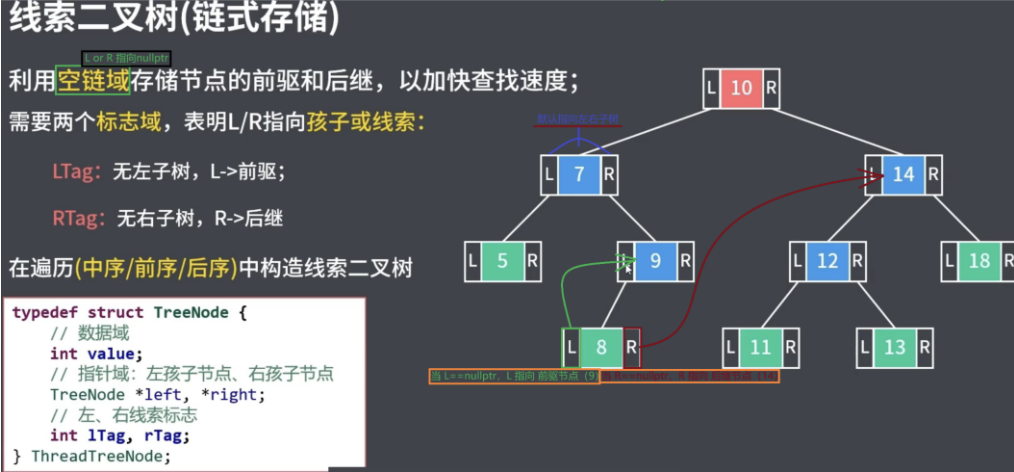
在这里插入图片描述

📝 节点结构定义

注意：度为 0/1 的节点才需线索化

C++// 线索标志typedef enum {CHILD, // 0THREAD // 1 节点指向nullptr}PointerTag; // 枚举：孩子 or 线索// 定义树节点的存储类型typedef int ElemType;typedef struct ThreadTreeNode{ElemType data;struct ThreadTreeNode* left, * right;// 线索标志默认为 0PointerTag ltag;PointerTag rtag;// 初始化字段 - 也要添加标志位初始化ThreadTreeNode(int val) : data(val), left(nullptr), right(nullptr), ltag(CHILD), rtag(CHILD){ }} ThreadTreeNode;

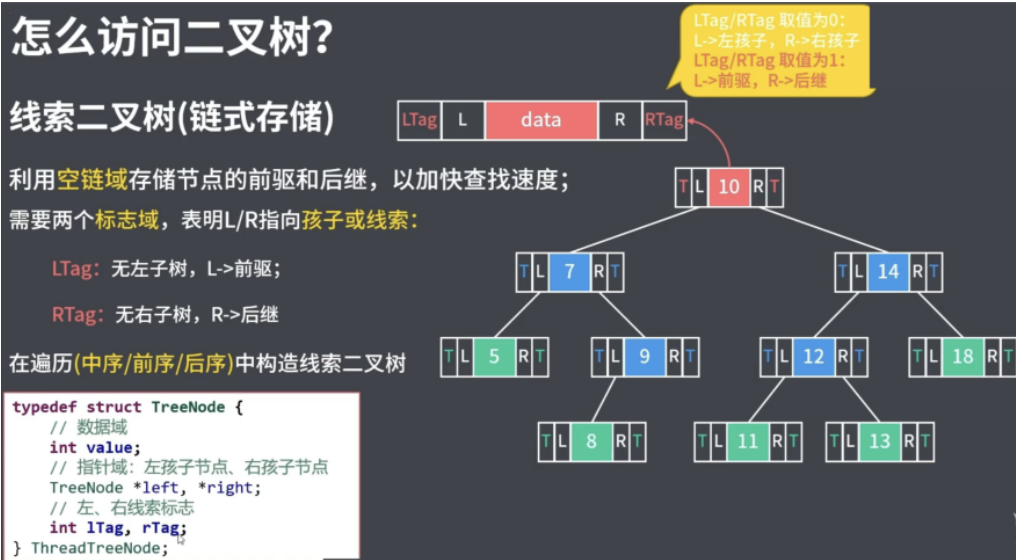
在这里插入图片描述

四、线索化二叉树

线索二叉树（链式存储）

一个二叉树想成为 线索二叉树，必须要基于遍历方式的基础上从而 线索化

注意：度为 0/1 的节点才需线索化

4.1前序遍历

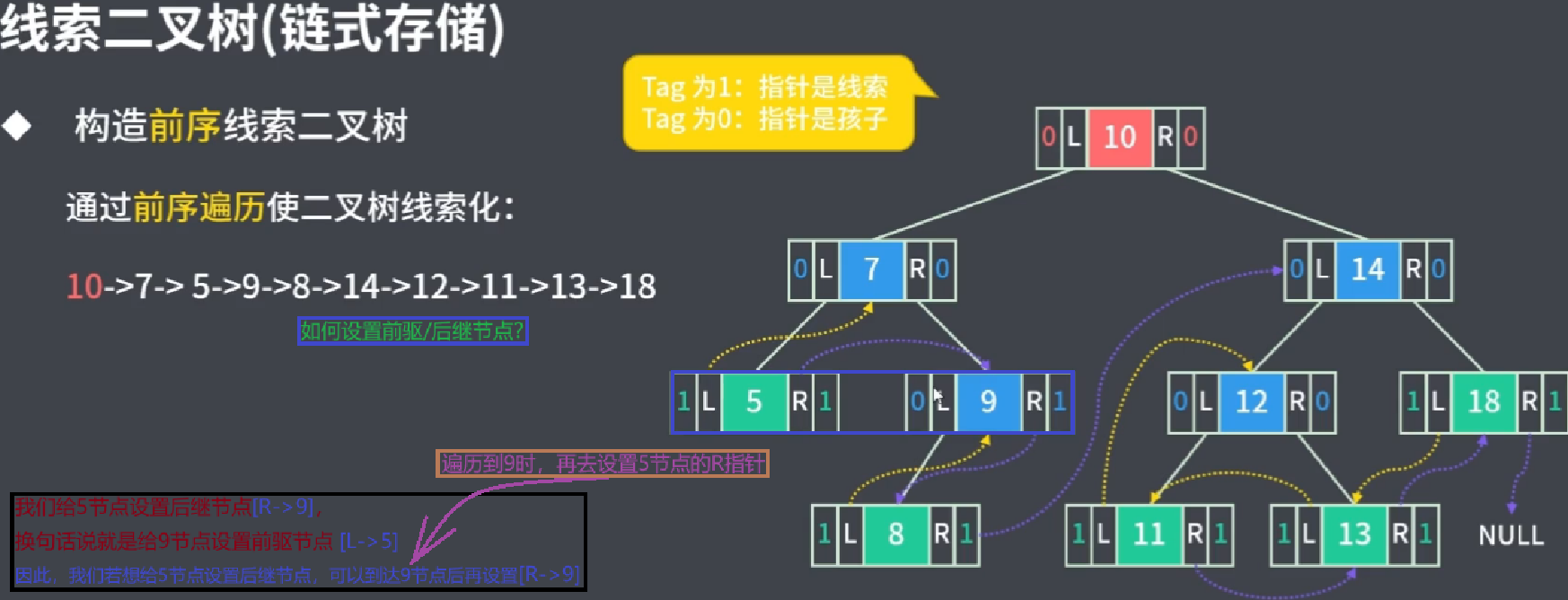
问：如何构造前序线索二叉树呢？
答：在对二叉树进行前序遍历的过程中，为二叉树的空链域线索化

⚡ 核心优势：高效遍历

普通二叉树前序遍历（需要栈）：

递归实现 OR 循环实现（显式使用栈）

线索二叉树前序遍历（无需栈）：

递归实现 OR 循环实现

4.1.1前序遍历线索化二叉树思路

第一步： 前序遍历为每个节点构造线索（使用前序遍历，实现二叉树线索化）

  • 1.定义全局变量：记录遍历过程中的前驱节点，PreNode = nullptr;

  • 2.使用前序遍历，递归式地为每一节点的空链域设置线索：

    • a.寻找空链域

    • b.为当前节点设置前驱节点

      b1.检查当前节点的左孩子节点是否为空
      若为空：建立当前节点的左指针线索，指向 PreNode（当前节点的前驱节点）
      若为不空：说明该节点是从根节点到当前路径上的任意一个节点，继续递归式访问左子树

    • c.为当前节点[A]设置后继线索[B]（准确的可以理解为：在后继节点[B]设置前驱节点[A]），即给后一节点设置前驱线索[不对，因为目前还未获取后一节点的信息！]；或：为当前节点[A]的前继节点[C]设置后继线索[C->A]
      c1.检查前一节点的右子树是否为空
      若为空：建立前一节点的右指针线索[C]，指向当前节点[C->A]
      若不为空：不做处理

    • d.迭代更新 PreNode，PreNode = A;（设置当前节点为前一节点）

  • 3.单独处理最后一个节点的右指针线索[默认指向 nullptr，修改rtag = 0]

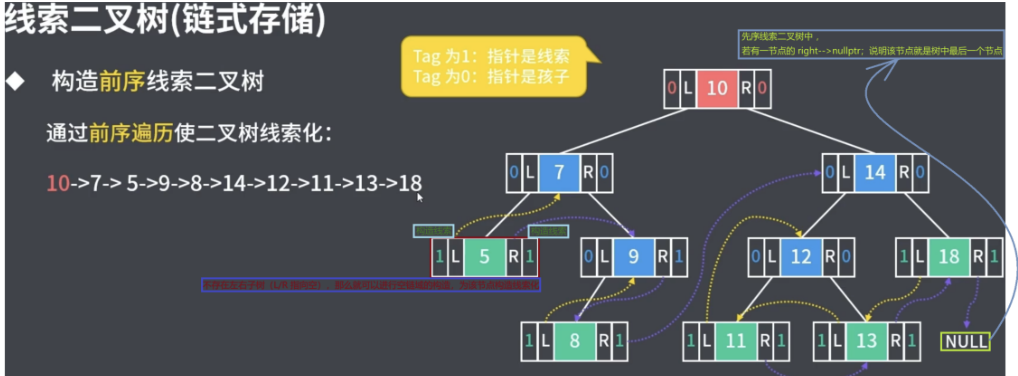
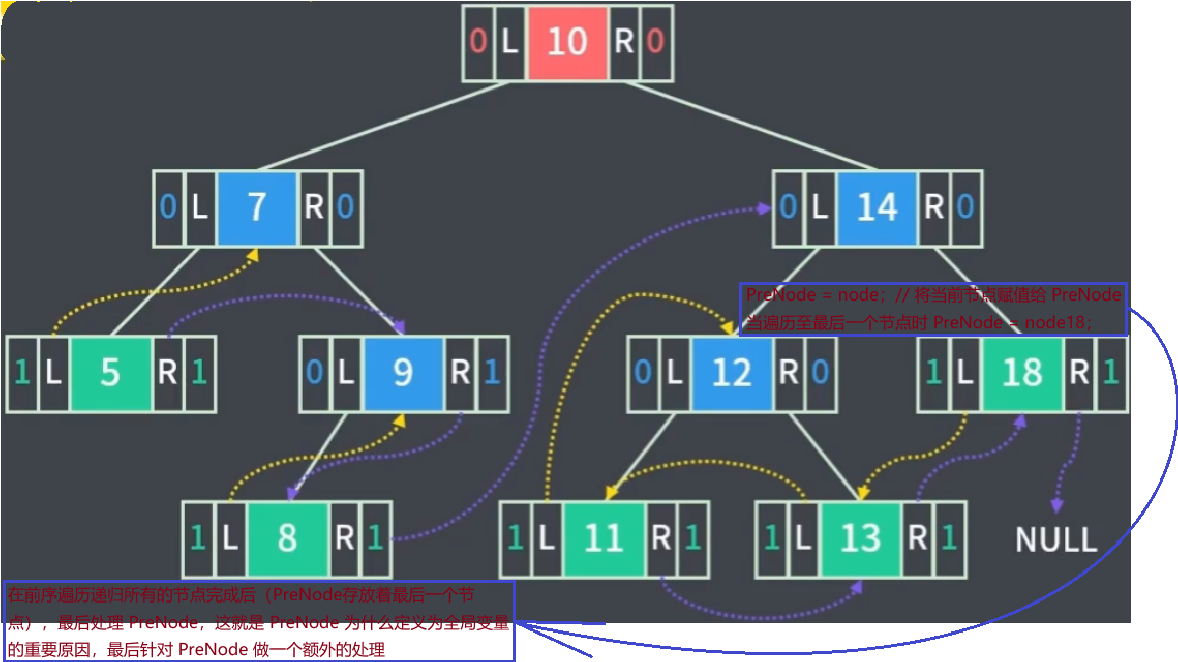
在这里插入图片描述

黄色：前驱指针

蓝色：后继指针

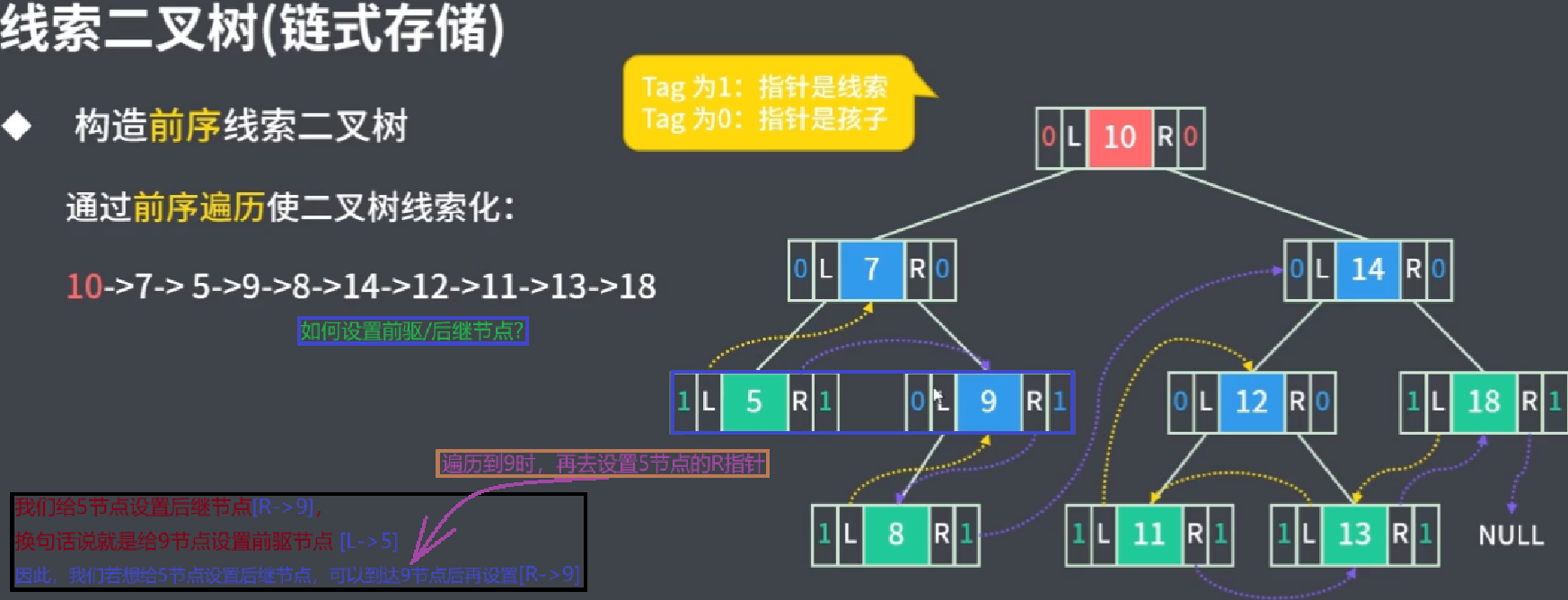
在这里插入图片描述

技巧：

  • 在当前节点A，设置A前驱：X<–A
  • 在当前节点的后一节点B，设置A后继：A–>B, A<–B
🎨 直观理解

原始二叉树：

        A(1)/   \B(2)  C(3)/   \D(4)  E(5)

空指针：D.left, D.right, E.left, E.right, C.left, C.right
前序遍历顺序：A(1) → B(2) → D(4) → E(5) → C(3)

前序线索化后（中序遍历：D→B→E→A→C→F）：

        A(1)/   \B(2) → C(3)/   \ D(4) → E(5) → C(3)
  • D.right → E (后继)
  • E.right → C (后继)
  • C.right → nullptr (最后一个节点)
4.1.2🔄前序遍历线索化二叉树实现

步骤1：定义全局变量，记录遍历过程中的前驱节点

C++ThreadTreeNode* PreNode = nullptr;

步骤2：前序遍历实现二叉树线索化（前序线索化递归函数）

// 前序遍历实现二叉树线索化
void PreOrderThread(ThreadTreeNode* node)
{if (node == nullptr) return;// 无需访问节点数据
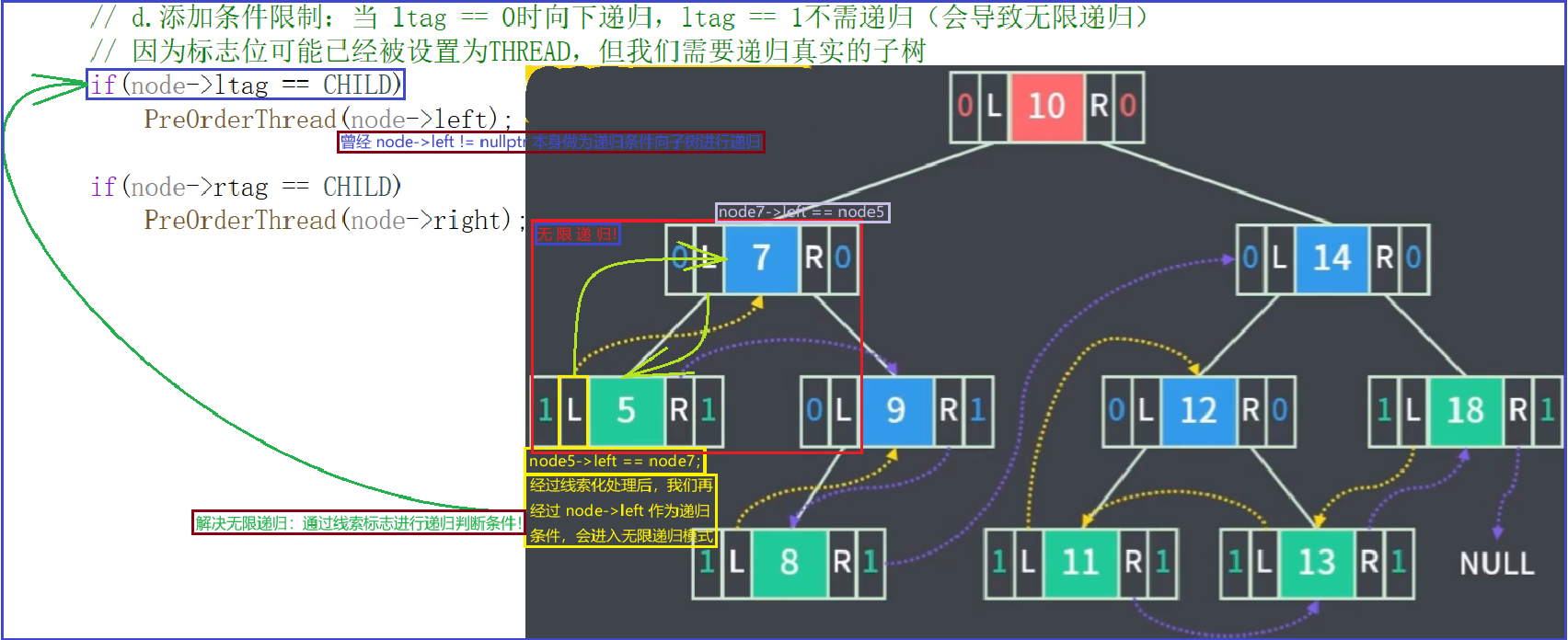
//    cout << node->data << "->"; 遍历目的：为空链域设置线索，将二叉树转变为线索二叉树// 2.递归式访问空链域// a.为当前节点设置前驱节点（如何为当前节点设置前驱节点？当前节点什么情况下需要设置前驱节点？）// 检查当前节点左子树是否为空if (!node->left){// 为空：建立当前节点的左指针线索，指向 PreNodenode->left = PreNode;// 更新标志位node->ltag = THREAD;}// b.为当前节点的前一节点设置后继线索（何时需要设置右指针线索？）// 检查当前节点右子树是否为空 && PreNode != nullptr（防止空指针异常）if (PreNode && !PreNode->right){PreNode->right = node;PreNode->rtag = THREAD;}// c.迭代更新 PreNodePreNode = node;cout << "----------- 此时就完成了对空链域的线索化 -----------" << endl;// d.添加条件限制：当 ltag == 0时向下递归，ltag == 1不需递归（会导致无限递归）// 因为标志位可能已经被设置为THREAD，但我们需要递归真实的子树if(node->ltag == CHILD)PreOrderThread(node->left);if(node->rtag == CHILD)PreOrderThread(node->right);
}

在这里插入图片描述

在这里插入图片描述

步骤3：二叉树线索化入口 - 实现二叉树线索化过程 与 最后节点处理过程分离（前序线索二叉树入口函数）

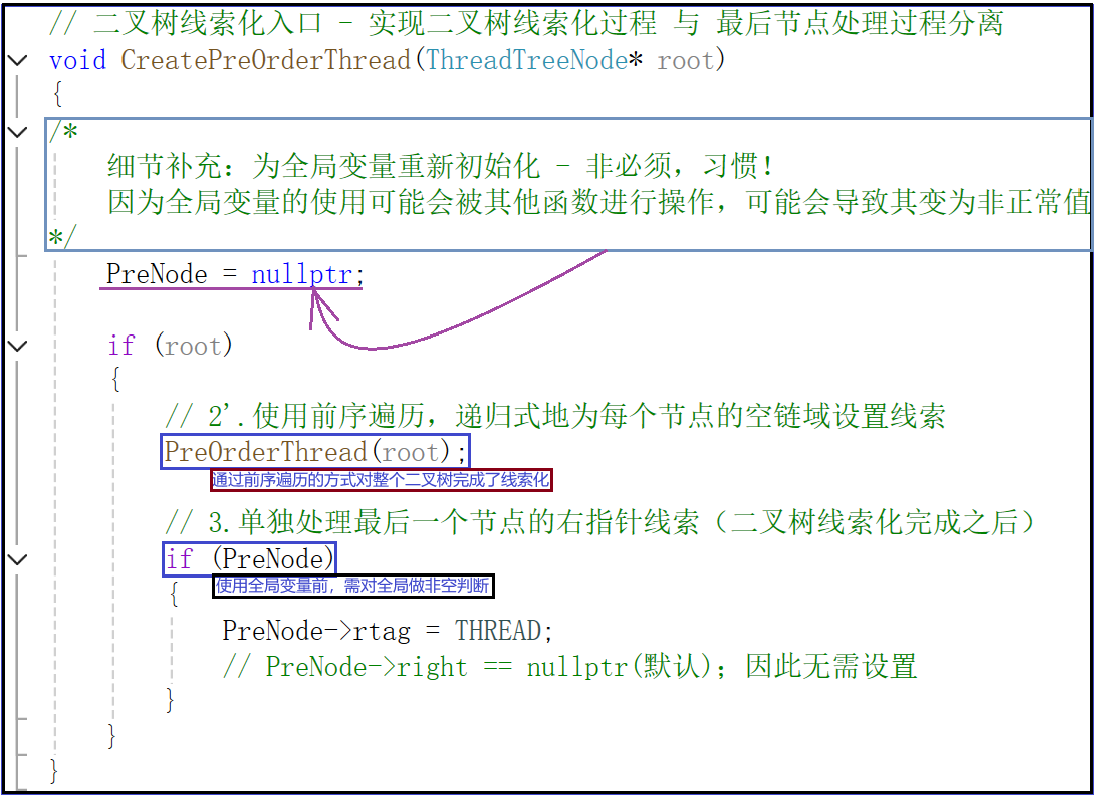
在这里插入图片描述

在这里插入图片描述

void CreatePreOrderThread(ThreadTreeNode* root)
{
/*细节补充：为全局变量重新初始化 - 非必须，习惯！因为全局变量的使用可能会被其他函数进行操作，可能会导致其变为非正常值
*/PreNode = nullptr;if (root){ // 2'.使用前序遍历，递归式地为每个节点的空链域设置线索PreOrderThread(root);// 3.单独处理最后一个节点的右指针线索（二叉树线索化完成之后）if (PreNode){PreNode->rtag = THREAD;// PreNode->right == nullptr(默认)；因此无需设置}
}

第二步： 2.定义函数，遍历 线索二叉树

🔍递归（Recursion）：

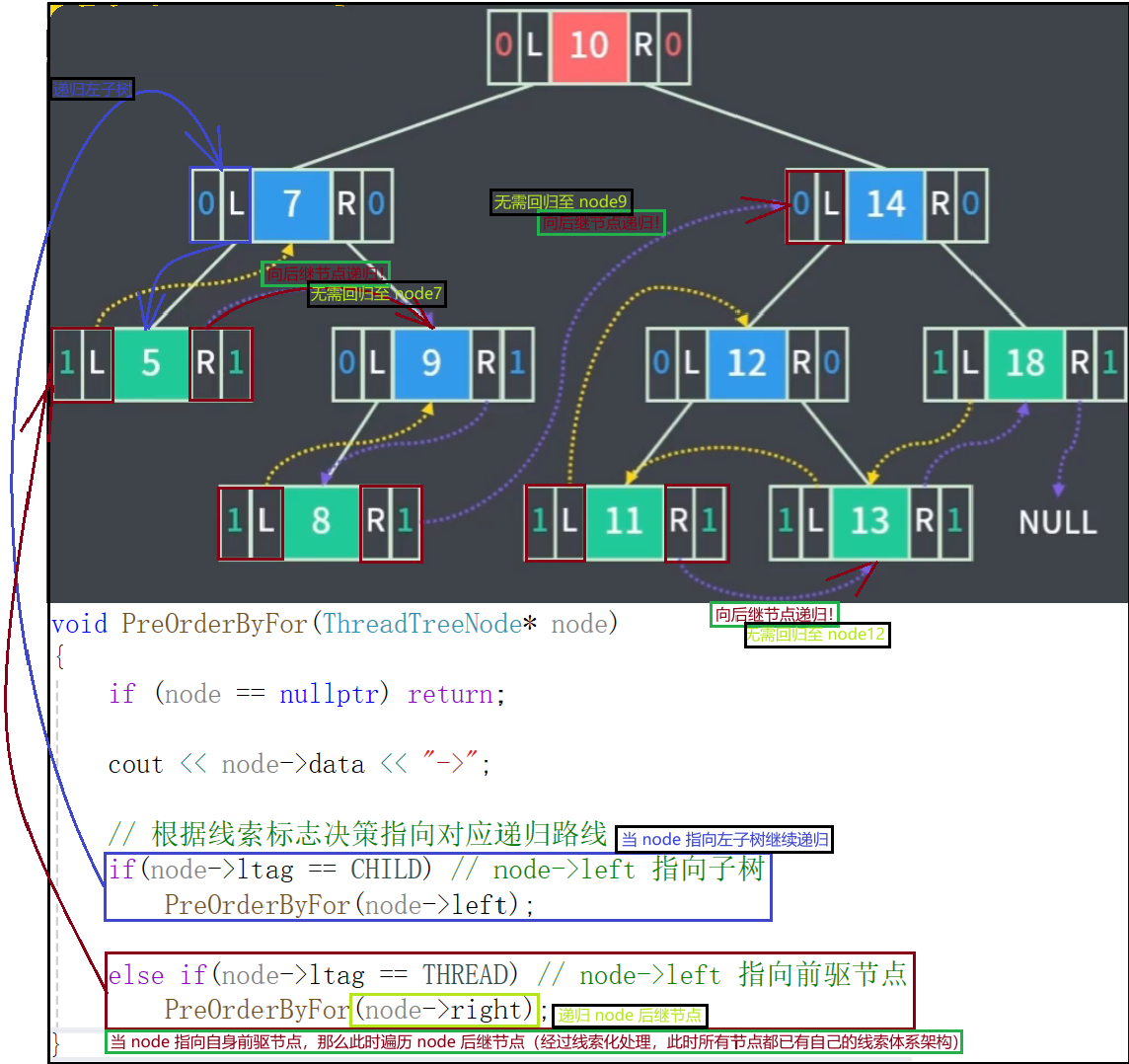
在这里插入图片描述

void PreOrderByRec(ThreadTreeNode* node)
{if (node == nullptr) return;cout << node->data << "->";// 根据线索标志决策指向对应递归路线if(node->ltag == CHILD) // node->left 指向子树PreOrderByRec(node->left);else if(node->ltag == THREAD) // node->left 指向前驱节点PreOrderByRec(node->right);
}

🔍循环（Circulate）：

void PreOrderByFor(ThreadTreeNode* node)
{ThreadTreeNode* cursor = node;while (cursor != nullptr){cout << cursor->data << "->";if (cursor->ltag == CHILD) // 向左子树循环cursor = cursor->left;else if (cursor->ltag == THREAD) // 向后继节点循环cursor = cursor->right;}
}

4.2中序遍历

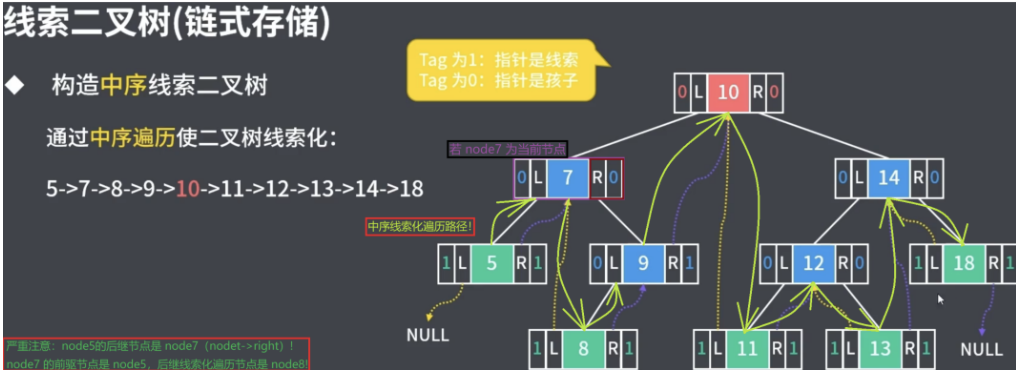
问：如何构造中序线索二叉树呢？
答：在对二叉树中序遍历的过程中，为二叉树的空链域进行线索化

重点：一定要分清前序线索化和中序线索化的区别！！！

在这里插入图片描述

在这里插入图片描述

4.2.1中序遍历线索化二叉树思路

核心思路：左–>根–>右

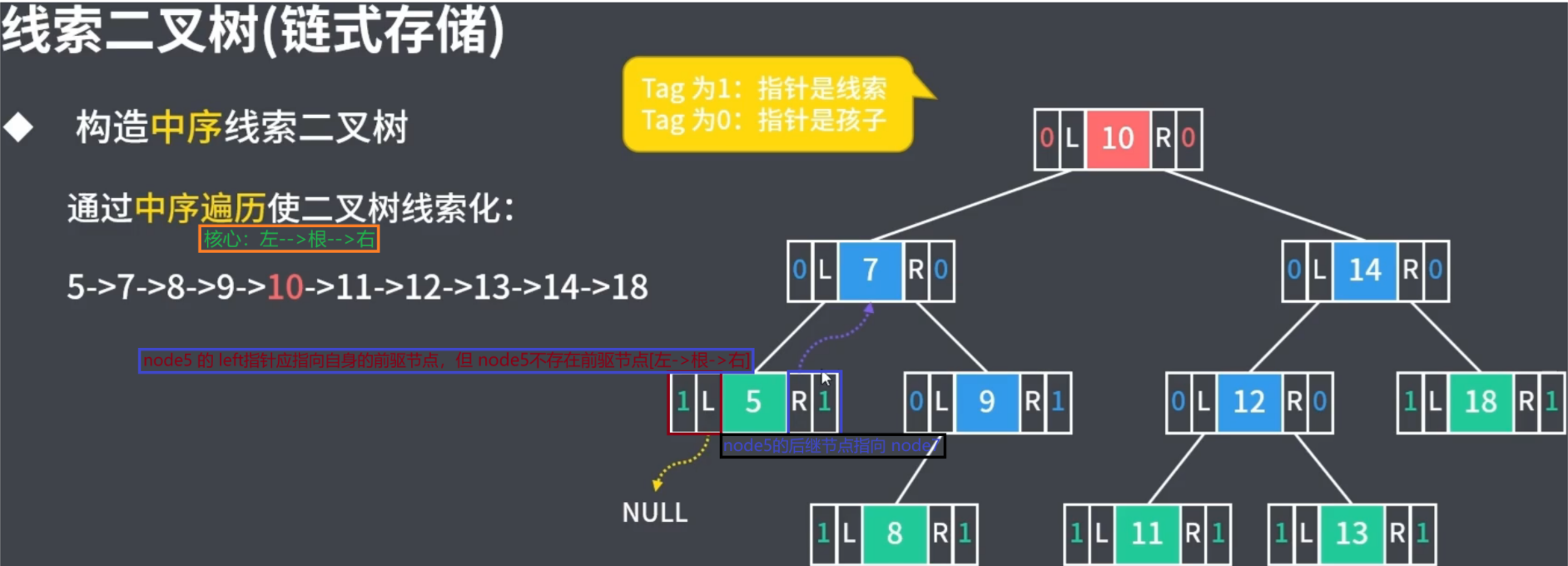
在这里插入图片描述

相比于前序线索二叉树，中序线索二叉树里并不只有一个节点指向 nullptr：firsrt–>left == nullptr；ultimate–>right = nullptr;

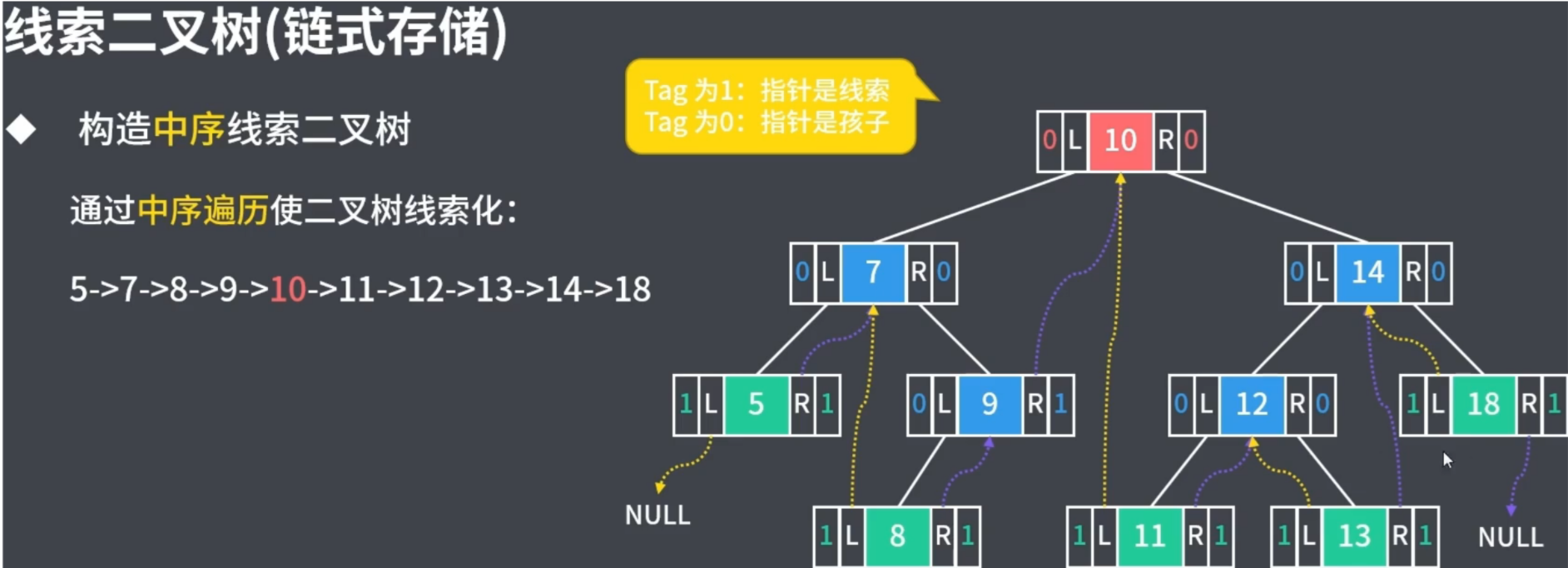
在这里插入图片描述

4.2.2🔄中序遍历线索化二叉树实现
ThreadTreeNode* PreNode = nullptr;void InOrderThread(ThreadTreeNode* node)
{if (node == nullptr) return;// 递归访问左子树InOrderThread(node->left);// a.设置前驱（此时 node == ultimate.node）if (!node->left){node->left = PreNode; // 默认值nullptrnode->ltag = THREAD;}// b.为当前节点的前驱节点设置后继线索if (PreNode && !PreNode->right){// 此时，PreNode 仍为 node的前继节点PreNode->right = node;PreNode->rtag = THREAD;}// c.迭代更新 PreNodePreNode = node;// 直接递归式访问后继节点，不会存在无限递归，所以无需添加条件限制InOrderThread(node->right); // node5->right == node7！因为中序遍历规则！578910...
}void CreateInOrderThread(ThreadTreeNode* root)
{PreNode = nullptr;if (root != nullptr){InOrderThread(root);if (PreNode)PreNode->rtag = THREAD;}
}// 前序遍历的首节点是根节点 - 中序遍历的首节点是左子树节点
void InOrderByFor(ThreadTreeNode* node)
{if (!node) return;// 1.获取第一个节点ThreadTreeNode* firstNode = node;while (firstNode->ltag == 0) // 可以使用 node->leftfirstNode = firstNode->left;// 2.依次访问线索二叉树的节点ThreadTreeNode* cursor = firstNode;// 易错：最后节点 nullptrwhile (cursor){// 访问节点数据cout << cursor->data << "->";/*如何找到当前节点的后继节点？- right指针指向的值：父节点 or 右子树需要区分当前节点的后继节点，即 node->right == 父节点？右子树？由于 rtag 的值不同，node->right 指向含义不同，因此需区分对待*/ if (cursor->rtag == CHILD){cursor = cursor->right;// 不能使用 cursor->left判断// 因为中序遍历的 node->left == nullptr；只出现在最左子树中while (cursor->ltag == 0)cursor = cursor->left;}else if (cursor->rtag == THREAD) // {cursor = cursor->right;}}
}

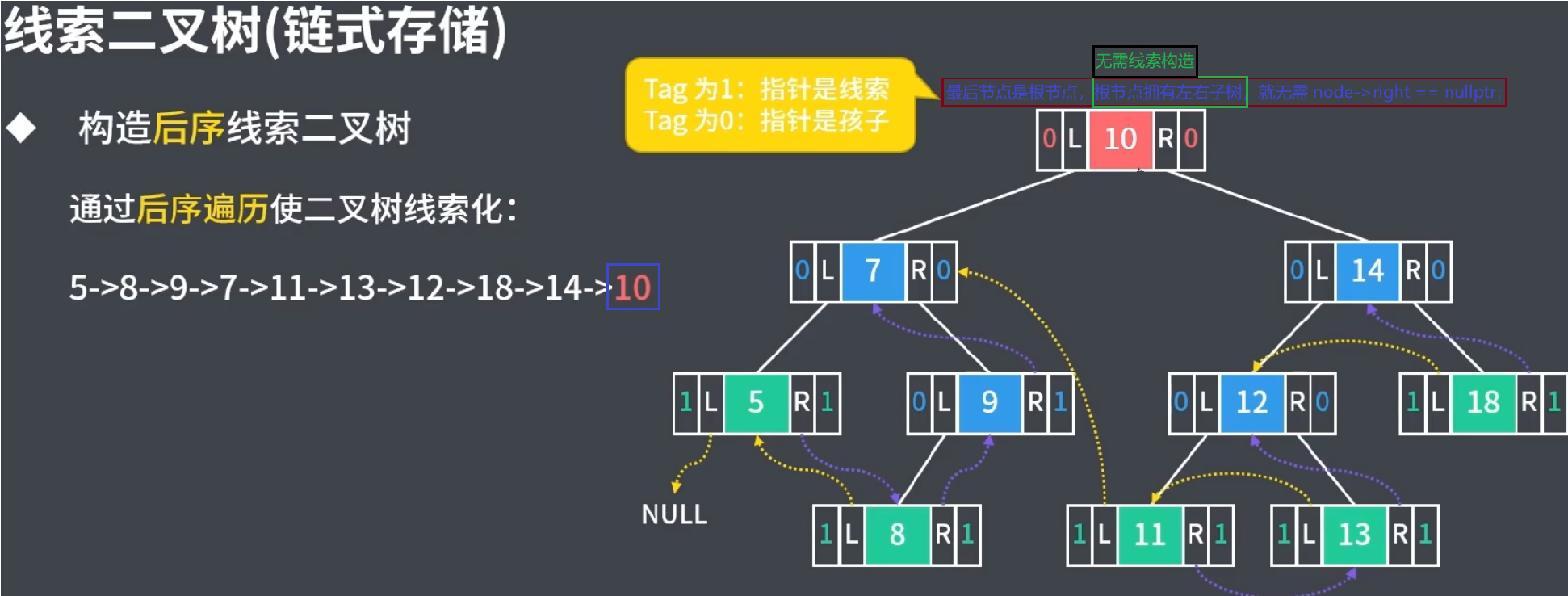
4.3后序遍历

问：如何构造后序线索二叉树呢？
答：在对二叉树后续遍历过程中，为二叉树空链域线索化

在这里插入图片描述

五、小结

📈 ✅性能对比
特性普通二叉树线索二叉树
空间利用率50%指针空闲100%指针利用
遍历空间复杂度O(h)O(1)
查找前驱/后继困难容易
插入/删除复杂度简单复杂
预处理无需需要一次线索化
灵活性高（支持多种遍历）低（特定遍历优化）
🎯 适用场景
  1. 频繁遍历但很少修改的数据
  2. 内存受限的环境
  3. 需要快速查找前驱/后继的操作
  4. 数据库索引结构
  5. 编译器语法树

推荐选择：

  • 普通二叉树：简单应用、多种遍历需求、内存充足
  • 前序线索二叉树：频繁前序遍历、内存受限、实时性要求高

线索二叉树 是"用编程复杂度换取运行效率"的典型例子

**线索二叉树的本质：**通过利用空指针域存储遍历顺序信息，实现：

  • ✅ 空间效率：100%指针利用率、
  • ✅ 时间效率：O(1)空间复杂度的遍历
  • ✅ 操作便利：快速查找前驱和后继

**代价：**插入和删除操作更复杂，需要维护线索关系

🌟 各位看官好，我是工藤新一¹呀~

🌈 愿各位心中所想，终有所致！

http://www.xdnf.cn/news/19081.html

相关文章：

  • 【C++】map 容器的使用
  • django配置多个app使用同一个static静态文件目录
  • Android Glide最佳实践：高效图片加载完全指南
  • 滥用Mybatis一级缓存引发OOM问题
  • 网络安全监控中心
  • 阿里云——计算服务深度解析与选型
  • ChatGPT 上线 “学习模式”：全版本开放，重构 AI 教育逻辑
  • 基于单片机步进电机控制电机正反转加减速系统Proteus仿真(含全部资料)
  • 北斗导航｜接收机自主完好性监测算法综述
  • java数据类型获取长度方式总结
  • SpringBoot集成 DeepSeek 对话补全功能
  • Spark学习记录
  • Unity 客户端和服务器端 基于网络的账户管理系统
  • 除自身以外数组的乘积是什么意思
  • 【OpenGL】LearnOpenGL学习笔记16 - 帧缓冲(FBO)、渲染缓冲(RBO)
  • 【JUC】——线程池
  • 点评项目（Redis中间件）第一部分Redis基础
  • docker run 后报错/bin/bash: /bin/bash: cannot execute binary file总结
  • 边缘计算：一场由物理定律发起的“计算革命”
  • 预测模型及超参数：2.传统机器学习：PLS及其改进
  • HarmonyOS 高效数据存储全攻略：从本地优化到分布式实战
  • 从 GRIT 到 WebUI：Chromium 内置资源加载与前端展示的完整链路解析
  • AI Agent 发展趋势与架构演进
  • 稳敏双态融合架构--架构师的练就
  • 【MES】工业4.0智能制造数字化工厂（数字车间、MES、ERP）解决方案：智能工厂体系架构、系统集成以及智能设计、生产、管理、仓储物流等
  • uvloop深度实践：从原理到高性能异步应用实战
  • http请求能支持多大内容的请求
  • 通义万相音频驱动视频模型Wan2.2-S2V重磅开源
  • 安卓接入通义千问AI的实现记录
  • 欧盟《人工智能法案》生效一年主要实施进展概览（二）