Python计算点云的欧式、马氏、最近邻、平均、倒角距离(Chamfer Distance)
今天我们系统介绍一下点云的几种距离计算方法。以下是对点云中五种常见距离度量的系统梳理,涵盖其定义、计算方法、核心特性与典型应用场景,便于快速查阅与对比:
---
1. 欧氏距离(Euclidean Distance)
1.1定义与公式
欧氏距离是最直观的距离度量,表示两点之间的“直线距离”。
对于三维点( p = (x_1, y_1, z_1)) 与 ( q = (x_2, y_2, z_2)),其公式为:
d(p, q) = sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2}1.2特点
- 对尺度敏感,所有维度权重相同
- 不考虑变量间的相关性1.3典型应用
- 点云配准(如 ICP 算法)
- 最近邻搜索(KNN、Radius Search)
- 点云降噪(识别孤立点)
- 下采样(体素邻域判断)
- 特征描述(如 FPFH、SHOT)
- 聚类与分割(DBSCAN、区域生长)---
2. 马氏距离(Mahalanobis Distance)
2.1定义与公式
马氏距离考虑了数据的**协方差结构**,适用于**多维相关特征空间**。
对于点 ( x ) 与分布均值 ( mu),协方差矩阵为( S ):
D_M(x) = sqrt{(x - mu)^T S^{-1} (x - mu)}2.2特点
- 消除量纲影响,考虑变量相关性
- 对异常值更鲁棒2.3典型应用
- 异常检测(识别偏离分布的点)
- 聚类分析(如 GMM、Mahalanobis K-means)
- 点云分割(结合统计分布的区域划分)
- 形状匹配(基于统计分布的相似性度量)---
3. 最近邻距离(Nearest Neighbor Distance)
3.1定义与计算方式
指某点到其“最近邻点”的距离,通常通过 KD-Tree 加速搜索。
可基于:
- K 近邻:距离第 K 个最近点的距离
- 半径邻域:在半径( r) 内的最近点距离3.2特点
- 反映局部点密度
- 对噪声敏感,需结合统计滤波3.3典型应用
- 异常检测(孤立点识别)
- 密度估计(局部点密度估计)
- 点云平滑(邻域加权平均)
- 预处理(去噪、下采样前清理)---
4. 平均距离(Average Neighbor Distance)
4.1定义与计算方式
指某点到其**邻域内所有点**的平均距离,常用作局部特征。
设邻域点集为( N(p)),则:
d_{avg}(p) = frac{1}{|N(p)|} sum_{q in N(p)} | p - q |_24.2特点
- 平滑局部密度变化
- 可用于特征提取与分类4.3典型应用
- 点云分类(作为几何特征输入)
- 地形分析(识别起伏变化)
- 工业检测(表面缺陷识别)---
5. 倒角距离(Chamfer Distance)
5.1定义与计算方式
衡量两个点云之间的**整体相似性**,定义为双向平均最短距离:
d_{CD}(A, B) = frac{1}{|A|} \sum_{a in A} \min_{b in B} | a - b |_2 + frac{1}{|B|} sum_{b in B} min_{a in A} | b - a |_25.2特点
- 对称、可微,适合深度学习
- 对点云密度不敏感5.3典型应用
- 点云重建质量评估(生成 vs 真实点云)
- 深度学习训练损失(如 3D 重建网络)
- 模型对齐(粗配准阶段)
下面给出几种方法的对比:
✅ 总结对比表
距离类型 | 是否考虑相关性 | 是否对尺度敏感 | 主要用途方向 |
| 欧氏距离 | 否 | 是 | 配准、聚类、降噪 |
| 马氏距离 | 是 | 否 | 异常检测、聚类、分割 |
| 最近邻距离 | 否 | 是 | 异常检测、密度估计 |
| 平均邻域距离 | 否 | 是 | 特征提取、分类、地形分析 |
| 倒角距离 | 否 | 否 | 重建评估、模型对齐 |
本次使用的数据依然是我们的老朋友——兔砸:
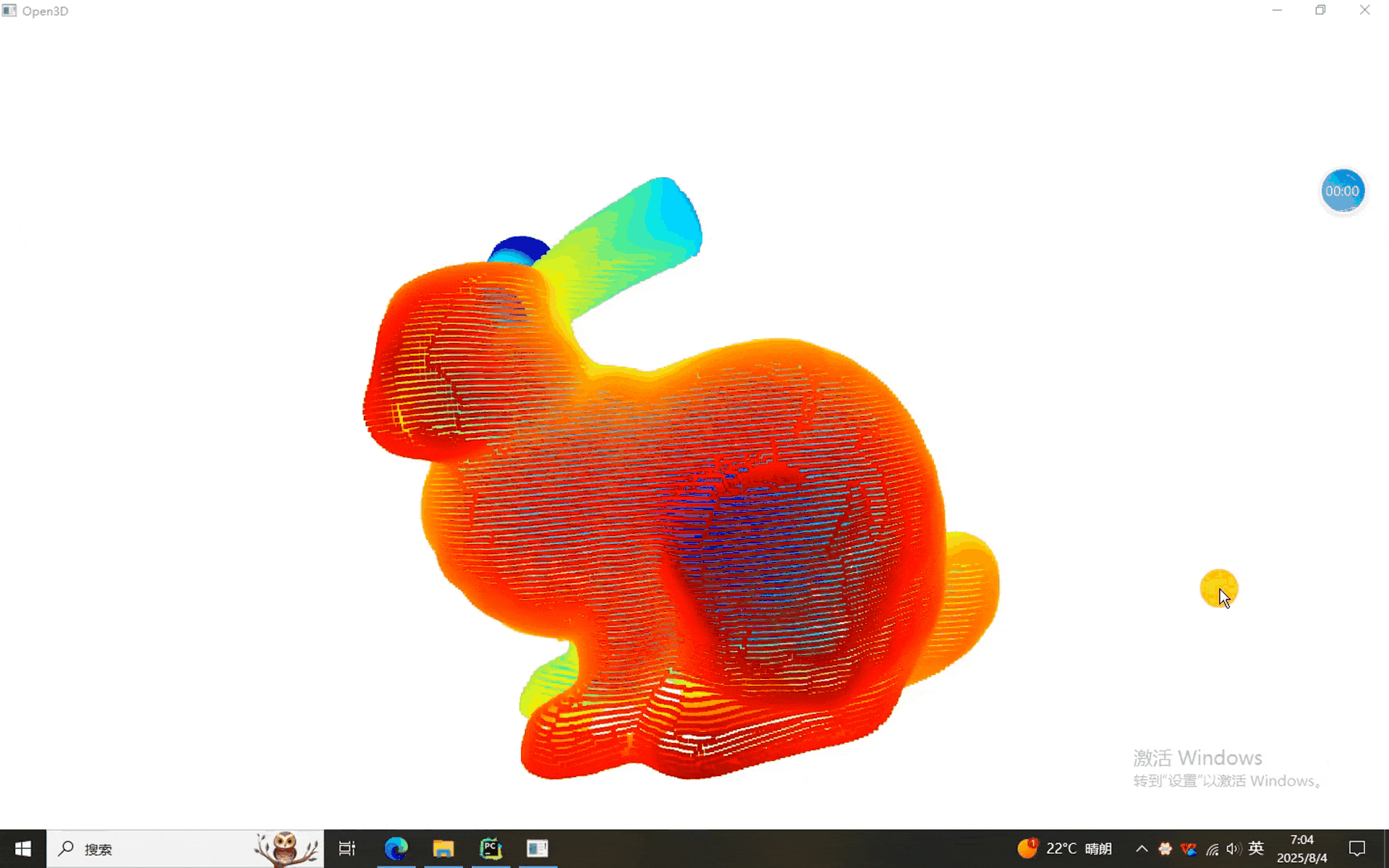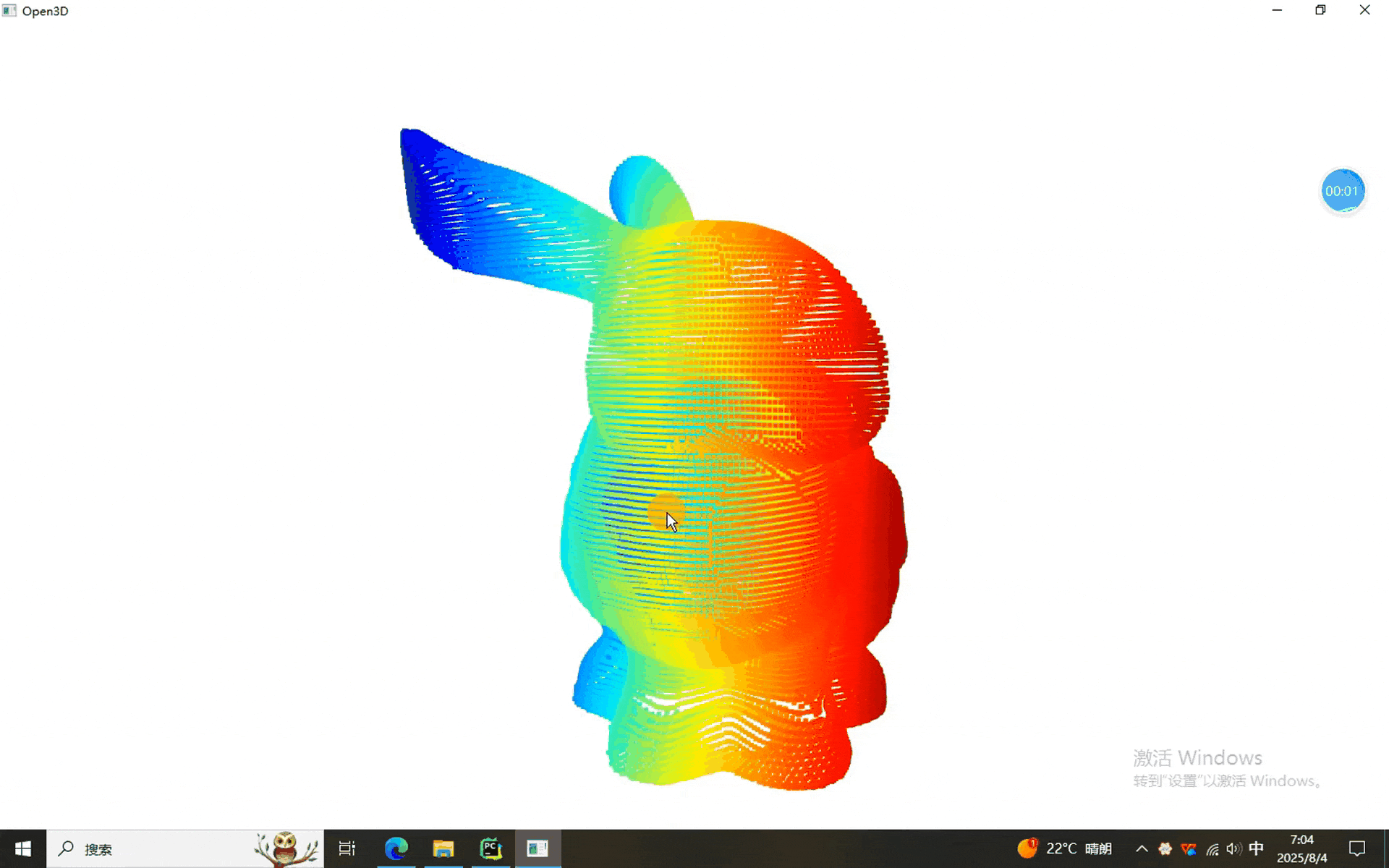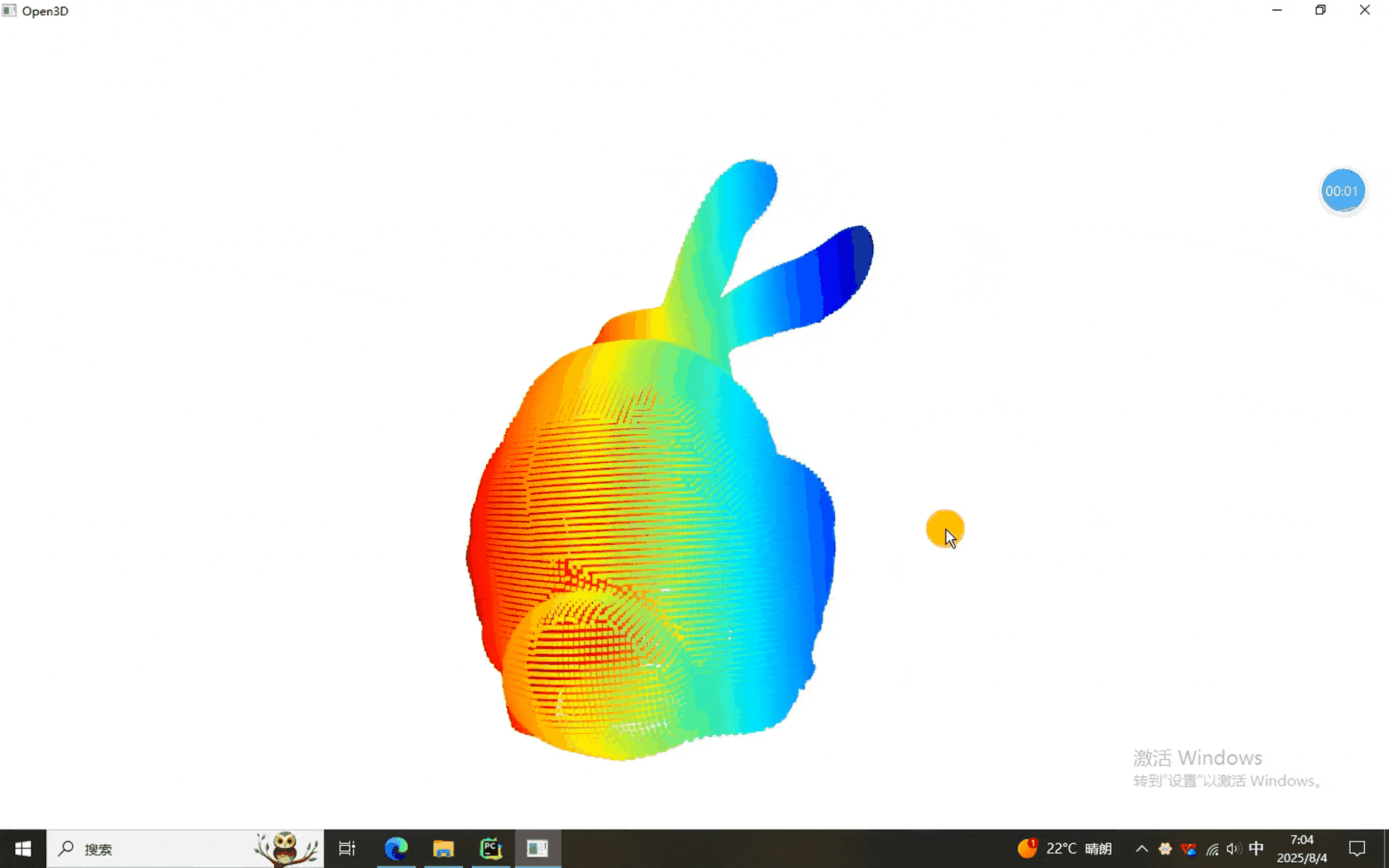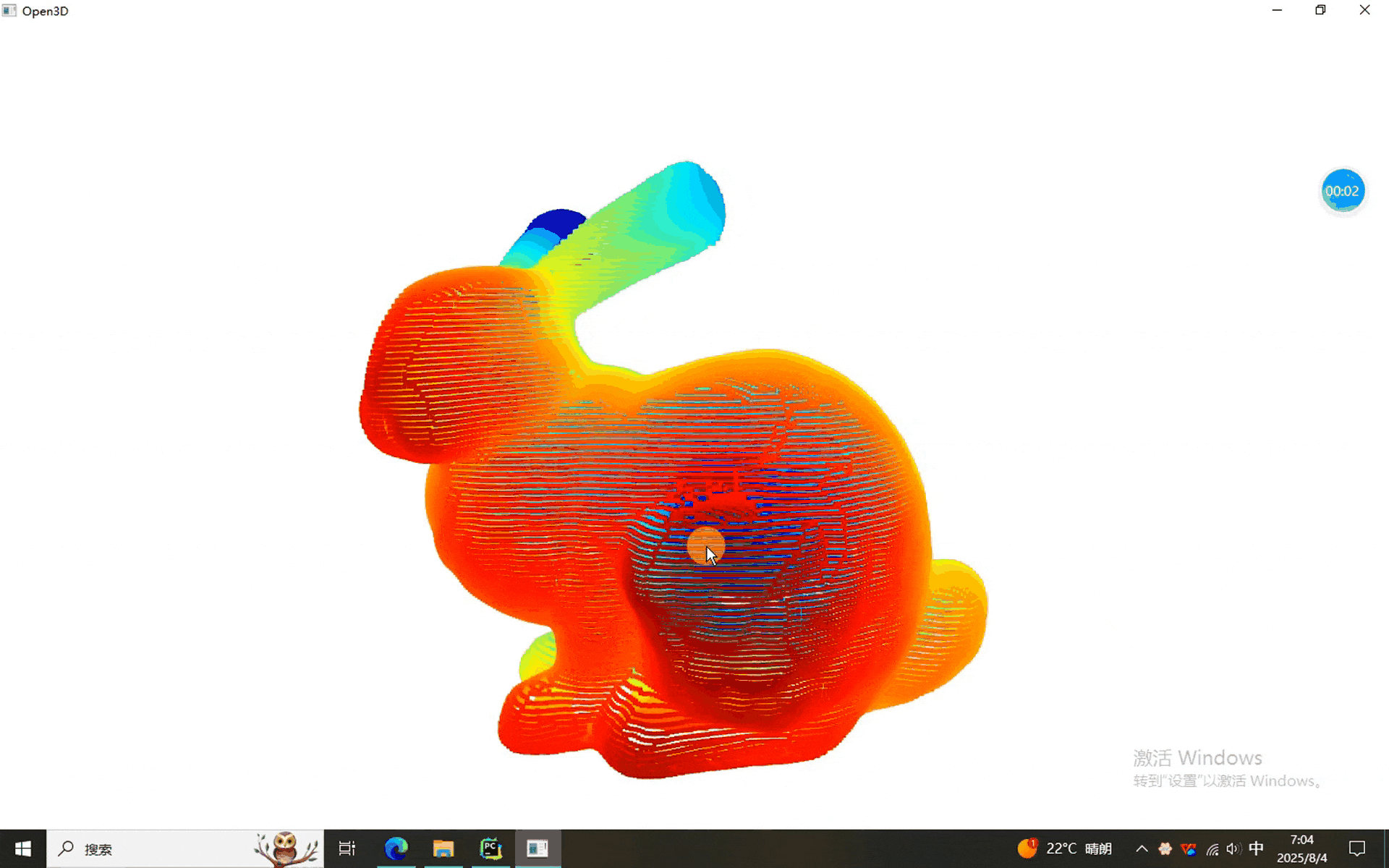
一、点云各种距离计算程序
import open3d as o3d
import numpy as np
import matplotlib.pyplot as plt
import sys
import os
import copy# -----------------------------------------------------------
# 工具函数
# -----------------------------------------------------------
def load_cloud(path):"""读取点云,失败就退出"""if not os.path.isfile(path):print(f"找不到文件:{path}")sys.exit(1)pcd = o3d.io.read_point_cloud(path)if pcd.is_empty():print(f"读取失败或点云为空:{path}")sys.exit(1)return pcddef color_by_values(pcd, values, cmap_name="jet"):values = np.asarray(values)norm = (values - values.min()) / (values.ptp() + 1e-12)colors = plt.get_cmap(cmap_name)(norm)[:, :3]pcd.colors = o3d.utility.Vector3dVector(colors)return pcd# -----------------------------------------------------------
# 菜单功能
# -----------------------------------------------------------
def euclidean_distance():print("\n--- 1. 欧氏距离 (source → target) ---")dists = np.asarray(source.compute_point_cloud_distance(target))print(f"平均欧氏距离:{dists.mean():.4f}")idx = np.where(dists > 0.09)[0]source_inlier = source.select_by_index(idx)o3d.visualization.draw_geometries([source_inlier])def mahalanobis_distance():print("\n--- 2. 马氏距离 (source) ---")md = source.compute_mahalanobis_distance()pcd_vis = color_by_values(source, md)o3d.visualization.draw_geometries([pcd_vis])def nearest_neighbor_distance():print("\n--- 3. 最近邻距离 (source) ---")dists = source.compute_nearest_neighbor_distance()pcd_vis = color_by_values(source, dists)o3d.visualization.draw_geometries([pcd_vis])def average_density():print("\n--- 4. 平均密度 (source) ---")dists = np.asarray(source.compute_nearest_neighbor_distance())densities = 1.0 / (dists + 1e-8)print(f"平均密度:{densities.mean():.4f}")pcd_vis = color_by_values(source, densities)o3d.visualization.draw_geometries([pcd_vis])def chamfer_distance():print("\n--- 5. 倒角距离 (source ↔ target) ---")d1 = np.asarray(source.compute_point_cloud_distance(target))d2 = np.asarray(target.compute_point_cloud_distance(source))chamfer = d1.sum() / len(source.points) + d2.sum() / len(target.points)print(f"倒角距离:{chamfer:.4f}")if __name__ == "__main__":# -----------------------------------------------------------# 一次性输入# -----------------------------------------------------------source_path = "E:/CSDN/规则点云/bunny.pcd"source = load_cloud(source_path)# 使用兔子生成第一个点云# 平移source_1 = copy.deepcopy(source)t = np.array([0.1, 0.15, 0.2])target = source_1.translate(t, relative=True) # relative=True 表示“增量”平移# -----------------------------------------------------------# 主循环# -----------------------------------------------------------menu = """请选择功能(1-6):1 欧氏距离2 马氏距离3 最近邻距离4 平均密度5 倒角距离6 退出>>> """func_map = {"1": euclidean_distance,"2": mahalanobis_distance,"3": nearest_neighbor_distance,"4": average_density,"5": chamfer_distance,}while True:choice = input(menu).strip()if choice in func_map:func_map[choice]()elif choice == "6":print("Bye~")sys.exit(0)else:print("请输入 1–6 之间的数字!")二、点云各种距离计算结果
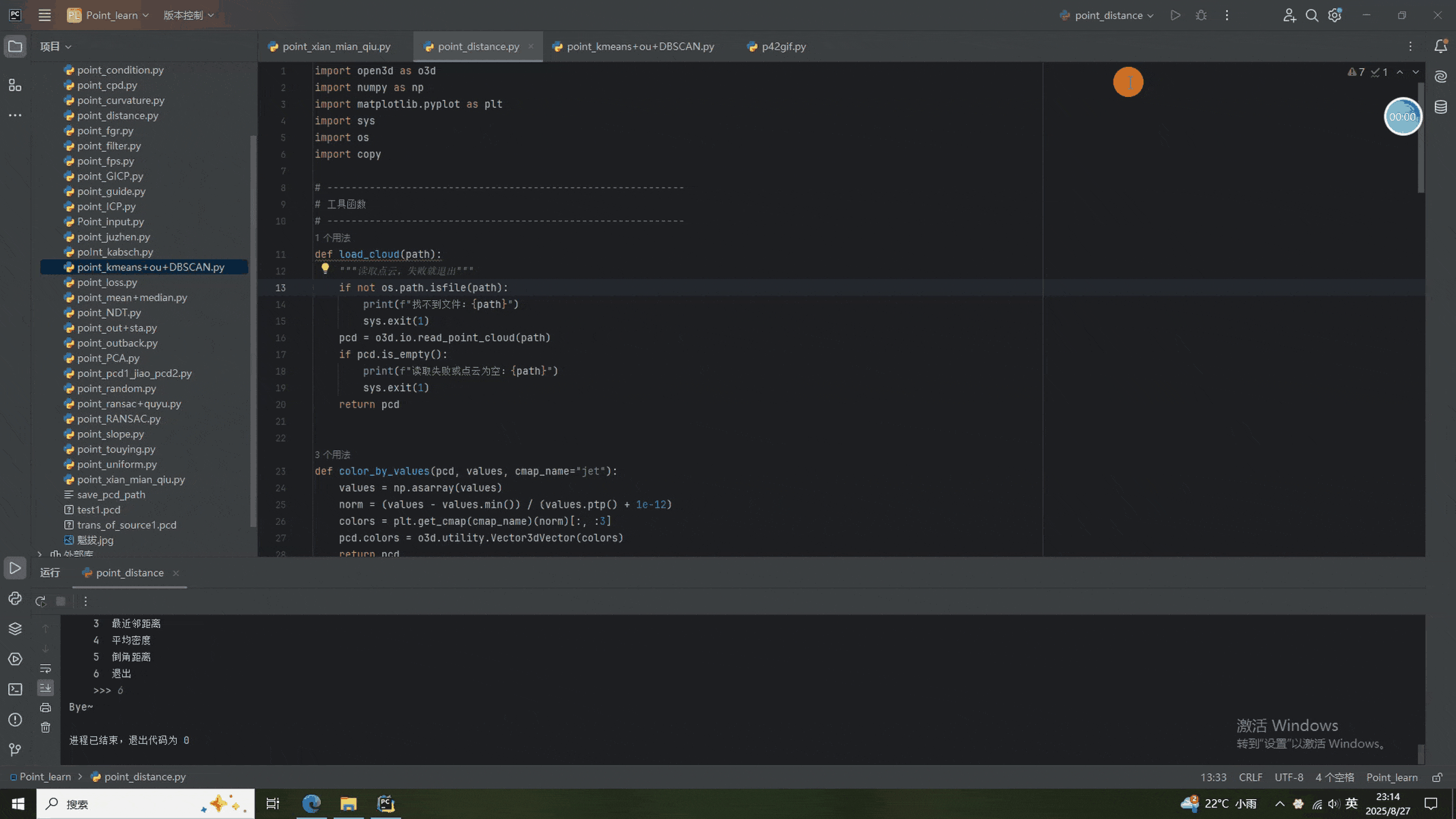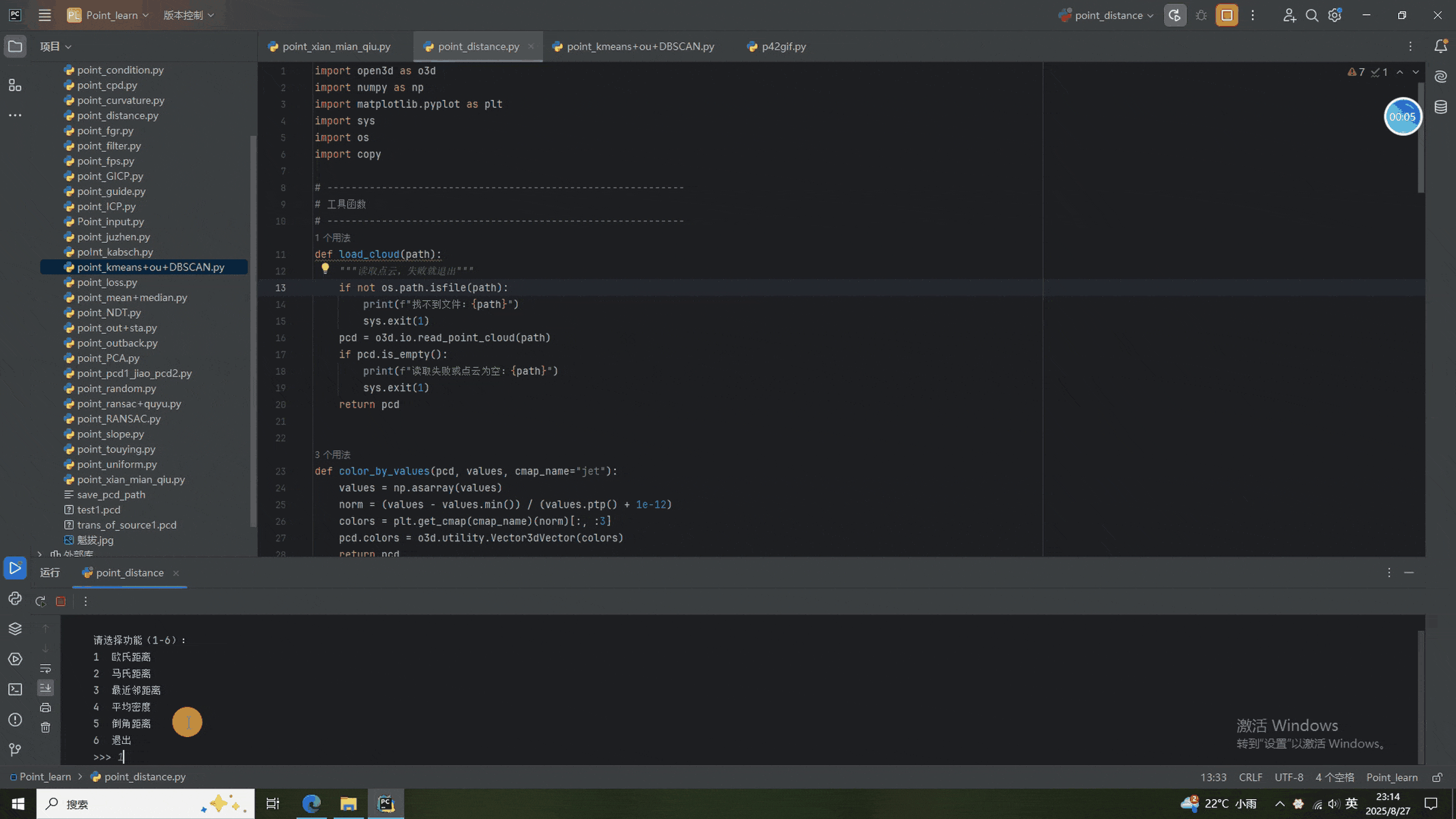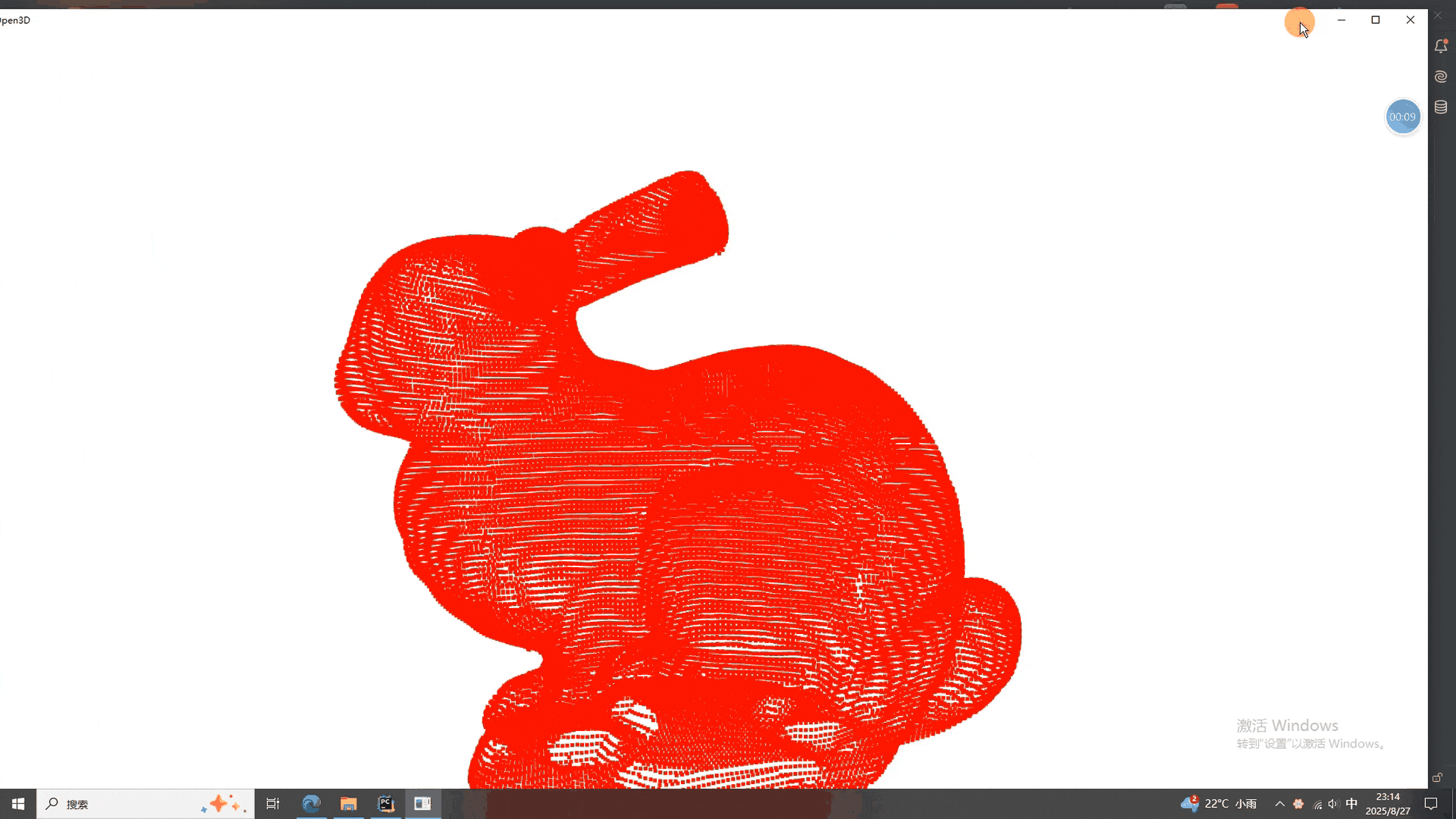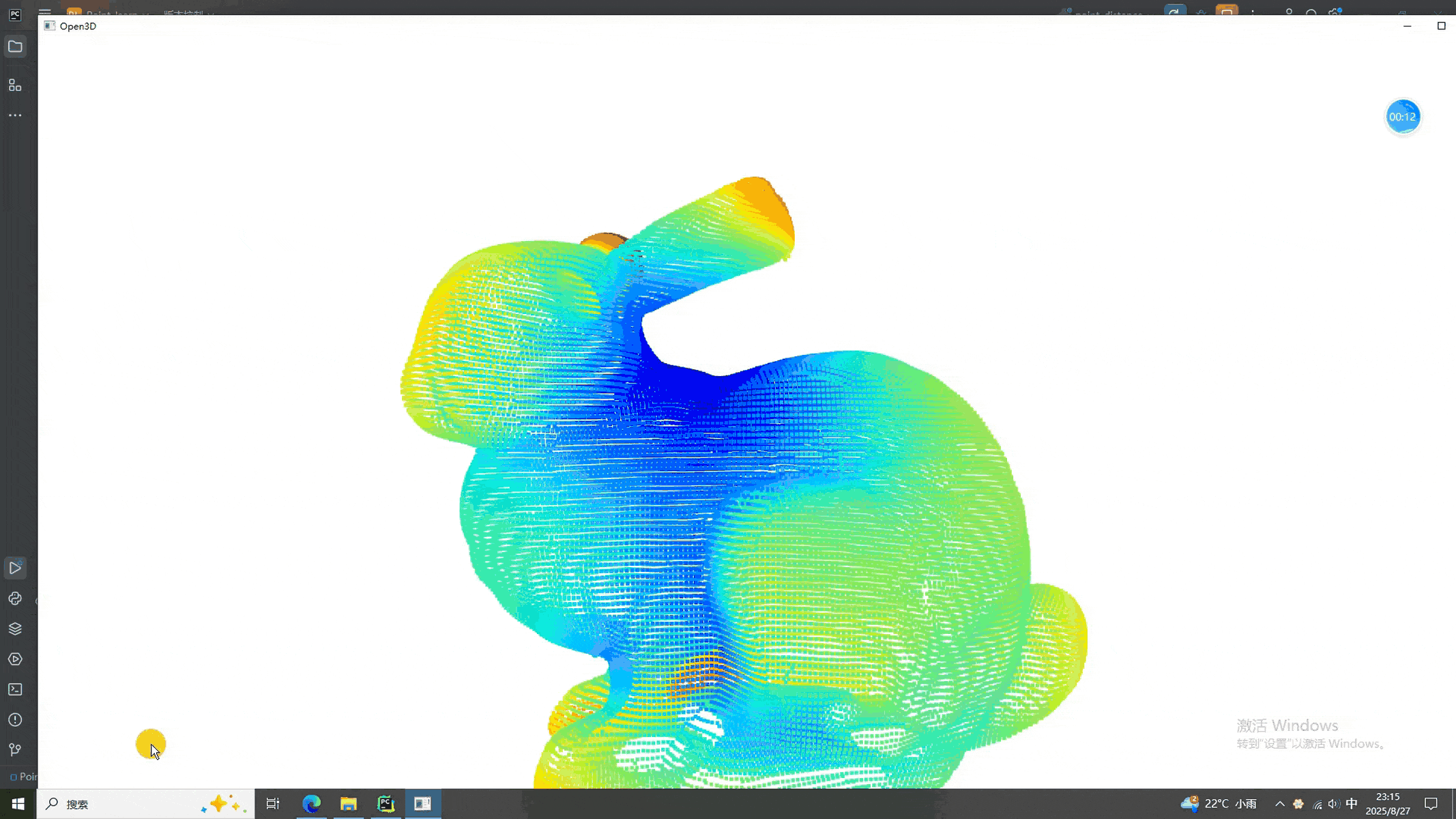
上述我们依然沿用了数字控制算法的选择,可以看出各种算法的结果都能计算出来(看出来个屁,就显示了两种)。需要单独使用的同学可以自行摘抄出来。。。
就酱,下次见^-^
