拓扑排序|hash

lc2929

枚举一个，另外两个

 res += (limit - (left - limit)) + 1;

上线-下线+1

class Solution {
public:
long long distributeCandies(int n, int limit)

{
long long res = 0;
for (int i = 0; i <= min(limit, n); ++i)

 {
// 第一个人拿了 i 个糖果
int left = n - i;

            // 剩下的两个孩子每人最多 limit，总共最多 2 * limit
if (left > 2 * limit)

            {
continue;
}

            // 如果 limit >= left，则第二个和第三个孩子可以自由组合分配 left 颗糖
if (limit >= left)

           {
res += left + 1;
}

      else {

                 res += (limit - (left - limit)) + 1;
}
}
return res;
}
};

lc403 memo

k-1/k/k+1   三分枝树 递归

记忆化搜索尝试青蛙每次跳k-1、k、k+1步

class Solution {
public:
vector<int> stones;
unordered_set<int> s;
bool canCross(vector<int>& stones) {
this->stones = stones;
return dfs(0, 0);
}

bool dfs(int k, int idx)
{
int key = idx * 1000 + k;
if (s.count(key) != 0) {
return false;
} else {
s.insert(key);
}

        vector<int> steps = {k - 1, k + 1, k};
for (int step : steps) {
if (step <= 0) continue;
int target = stones[idx] + step;

for (int i = idx + 1; i < stones.size(); ++i) {
  if (stones[i] == target) {
if (dfs(step, i)) {
return true;
}
break;
}

               else if (stones[i] > target) {
break;
}
}
}

        return idx == stones.size() - 1;
}
};

lc17.19

出现了的元素*-1标记，原地hash，最后检查凡是>0的就是没出现过的

类似题lc442

class Solution {
public:
vector<int> missingTwo(vector<int>& nums) {
int n = nums.size()+2; // 1-n
nums.push_back(1);     //增加两个对齐，简化后续处理
nums.push_back(1);
for(int i = 0;i<n;i++)
{
nums[abs(nums[i])-1] *= -1; //将所有出现过的数作为索引，并将索引后的值取负作为标记
}

vector<int> ret;
for(int i = 0;i<n;i++)
{
if(nums[i]>0)   ret.push_back(i+1); //凡是没有被标记的就是没出现过的
}
return ret;
}
};

lc1203

组内+组间  两次拓扑排序

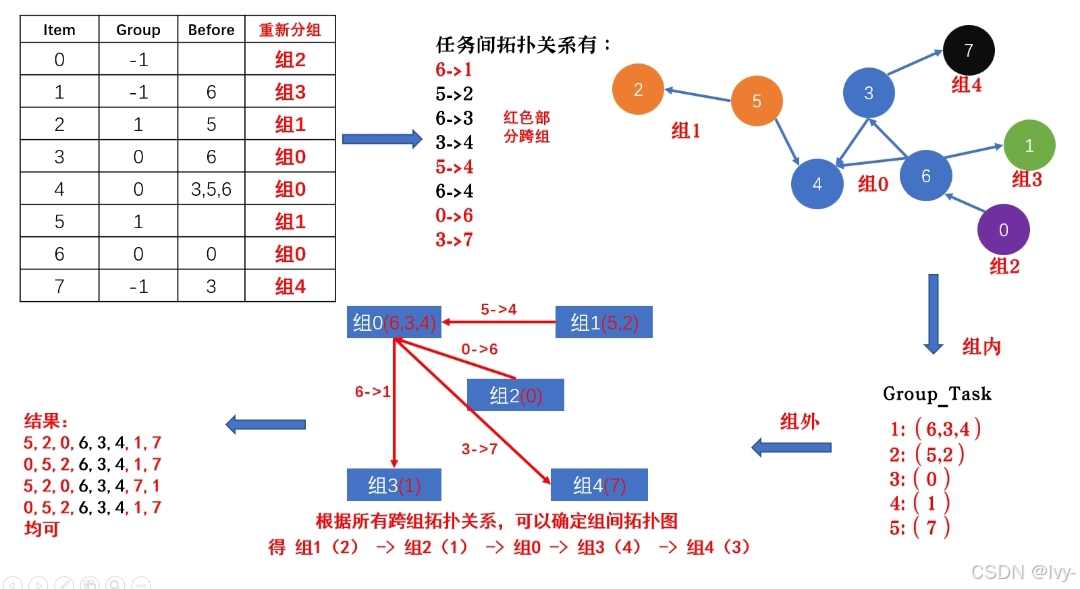
对项目任务进行排序，解决的是带有依赖关系（ befores ）和分组（ group ）的任务排序问题

整体思路是通过两层拓扑排序实现的：先对每个小组内的任务排序，再对小组之间的顺序排序。

核心逻辑概述

假设有 n 个任务、 m 个小组，每个任务属于一个小组（或独立成组），且部分任务有前置依赖（必须先完成前置任务才能执行当前任务）。

1. 处理独立任务（不属于任何小组的任务），为其创建虚拟组。

2. 对每个小组内部的任务进行拓扑排序，确保组内任务满足依赖关系

3. 对所有小组之间的顺序进行拓扑排序，确保不同组的任务依赖关系被满足。

4. 结合小组排序结果和组内任务排序结果，得到最终的任务执行顺序。

详细代码

1. 成员变量

-  unordered_map<int, vector<int>> sub ：存储每个小组（或虚拟组）内排好序的任务列表，键是组号，值是该组内按依赖关系排序后的任务ID。

2. 主函数  sortItems 

该函数是排序的核心流程，分为4个关键步骤：

步骤1：处理独立任务，创建虚拟组

for (int j = 0; j < n; j++)

{
if (group[j] == -1) group[j] = m++;
}


- 原数据中 group[j] = -1 表示任务 j 不属于任何小组，这里为其分配新的组号（从 m 开始递增），确保每个任务都有明确的组。

步骤2：按小组分组任务

vector<vector<int>> gg(m);
for (int j = 0; j < n; j++) gg[group[j]].push_back(j);


- 创建二维数组 gg ， gg[i] 存储第 i 个小组包含的所有任务ID，方便后续对组内任务排序。

步骤3：对每个小组内的任务进行拓扑排序

for (int i = 0; i < gg.size(); i++)

{
if (gg[i].size() == 1)

   {
// 组内只有1个任务，直接加入结果，无需排序
sub[group[gg[i][0]]] = {gg[i][0]};
continue;
}
// 调用拓扑排序函数，若失败（有环）返回空
bool f = topoSort(i, gg[i], befores);
if (!f) return {};
}


- 对每个小组 i ，若组内只有1个任务，直接存入 sub ；否则调用 topoSort 进行组内排序。
- 若排序失败（存在循环依赖，如A依赖B，B依赖A），返回空列表表示无法排序。

步骤4：对小组之间的顺序进行拓扑排序

// 准备小组的依赖关系
vector<int> groups; 
for (int i = 0; i < m; i++) groups.push_back(i); // 所有小组的ID列表
vector<vector<int>> newbefore(m); // 小组之间的依赖关系

for (int i = 0; i < n; i++) {
for (int j = 0; j < befores[i].size(); j++)

{
int prevId = group[befores[i][j]]; // 前置任务所属的组
if (prevId != group[i]) { // 若前置任务属于其他组，则当前组依赖前置组
newbefore[group[i]].push_back(prevId);
}
}
}

// 对小组进行拓扑排序，若失败返回空
if (!topoSort(m, groups, newbefore)) return {};

// 组合结果：按小组排序结果，依次拼接每个组的任务列表
vector<int> rs;
for (auto v : sub[m])    rs.insert(rs.end(),sub[v].begin(),sub[v].end());

return rs;


- 先构建小组之间的依赖关系 newbefore ：若任务 i 依赖任务 j ，且 i 和 j 属于不同组，则 i 所在的组依赖 j 所在的组。
- 调用 topoSort 对所有小组进行排序（这里用 m 作为临时键存储小组排序结果）。
- 最后按小组排序结果，依次拼接每个组内已排好序的任务，得到最终结果。

3. 拓扑排序函数  topoSort 

该函数是通用的拓扑排序实现，用于对一组节点（可以是任务或小组）按依赖关系排序：

bool topoSort(int gpid, vector<int>& num, vector<vector<int>>& bef) {
int n = num.size();
unordered_map<int, int> degree; // 记录每个节点的入度（依赖的前置节点数量）
unordered_map<int, vector<int>> g; // 邻接表：记录节点的后置节点（依赖当前节点的节点）

// 初始化入度和邻接表
for (int i = 0; i < n; i++) {
degree[num[i]] = 0;
g[num[i]] = vector<int>();
}

// 计算入度和构建邻接表
for (int i = 0; i < n; i++) {
int idx = num[i];
for (int j = 0; j < bef[idx].size(); j++) {
int last = bef[idx][j]; // 前置节点
if (degree.count(last)) { // 若前置节点在当前排序范围内
g[last].push_back(idx); // 前置节点指向当前节点
degree[idx]++; // 当前节点入度+1
}
}
}

// 拓扑排序队列：先加入所有入度为0的节点（无前置依赖）
queue<int> q;
for (int i = 0; i < n; i++) {
if (degree[num[i]] == 0) q.push(num[i]);
}

// 执行排序
vector<int> res;
while (!q.empty()) {
int cur = q.front();
q.pop();
res.push_back(cur); // 加入结果
// 遍历当前节点的后置节点，入度-1，若入度为0则加入队列
for (int next : g[cur]) {
if (--degree[next] == 0) q.push(next);
}
}

// 存储排序结果，若结果长度等于节点数则排序成功（无环）
sub[gpid] = move(res);
return sub[gpid].size() == n;
}


- 核心原理：通过入度（ degree ）记录每个节点的依赖数量，用队列依次处理入度为0的节点（无依赖），并更新其后续节点的入度，最终若所有节点都被处理则无环，排序成功。

总结

这段代码通过“先组内排序，再组间排序”的两层拓扑排序策略，高效解决了带分组和依赖的任务排序问题，确保最终的任务序列同时满足组内、组间的所有依赖关系。若存在循环依赖（无法排序），则返回空列表。