曲面方程的三维可视化:从数学解析到Python实现
在三维几何建模中,我们经常遇到需要将隐式方程可视化的需求。本文将深入探讨一个特定的曲面方程:
XH−YH2+ZH2tan(θ)−H2πarcsin(YHYH2+ZH2)=0 X_H - \frac{\sqrt{Y_H^2 + Z_H^2}}{\tan(\theta)} - \frac{H}{2\pi} \arcsin\left( \frac{Y_H}{\sqrt{Y_H^2 + Z_H^2}} \right) = 0 XH−tan(θ)YH2+ZH2−2πHarcsin(YH2+ZH2YH)=0
这个方程在机械工程、计算机图形学和数学建模中具有重要应用,特别是在描述螺旋曲面和旋转曲面时。
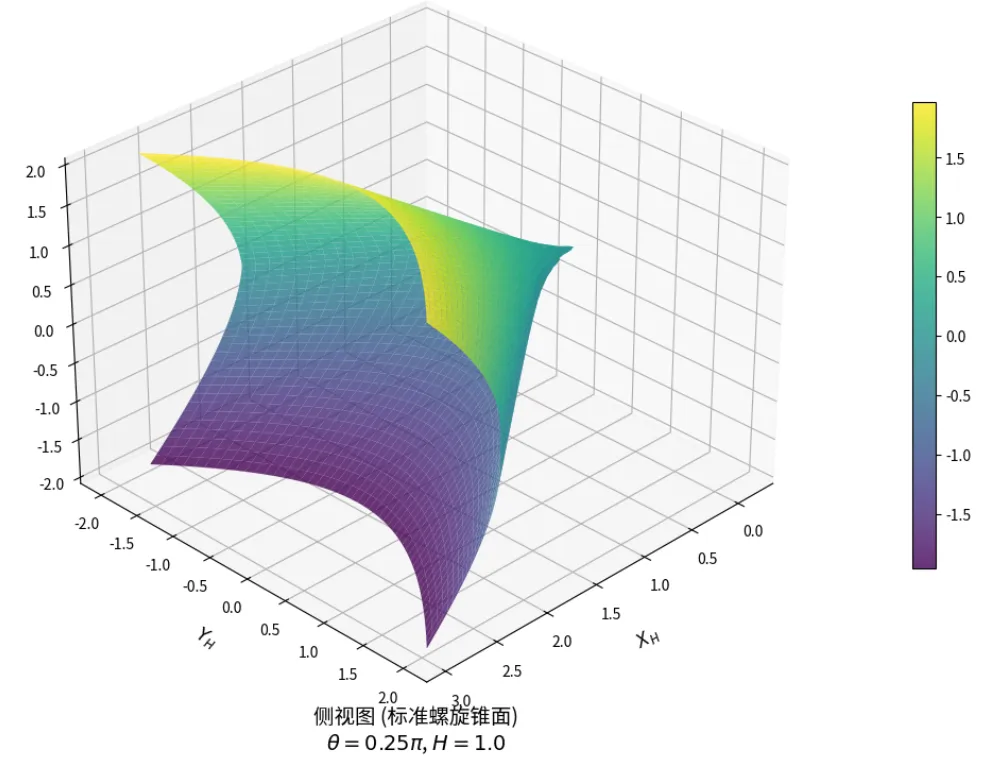
数学解析与变换
首先,我们将原方程重写为显式形式:
XH=YH2+ZH2tan(θ)+H2πarcsin(YHYH2+ZH2) X_H = \frac{\sqrt{Y_H^2 + Z_H^2}}{\tan(\theta)} + \frac{H}{2\pi} \arcsin\left( \frac{Y_H}{\sqrt{Y_H^2 + Z_H^2}} \right) XH=tan(θ)YH2+ZH2+2πHarcsin(YH2+ZH2YH)
这个表达式揭示了曲面的几何特性。第一项 YH2+ZH2tan(θ)\frac{\sqrt{Y_H^2 + Z_H^2}}{\tan(\theta)}tan(θ)Y
