数学建模——非线性规划
1.概念
非线性规划(Nonlinear Programming, NLP)是数学建模中用于解决目标函数或约束条件至少有一个为非线性的优化问题。与线性规划不同,非线性规划能处理更复杂的现实问题,如工程设计、经济学中的效用最大化等。
| 线性规划 | 非线性规划 | |
| 相同点 |
| |
| 数学形式 | 目标函数与约束均为线性(如 ax+by≤c) | 目标函数或约束存在非线性(如 x2+sin(y)≤10) |
| 应用典型 | 资源分配、运输问题(如最小成本流) | 工程设计、金融组合优化(如带风险惩罚的收益最大化) |
| 最终结果 | 可以直接给出整体最优解 有特定的方法 并且最优解一定是在边界上 | 只能先求局部最优解,找近似解 目前没有适合各种问题的通用解法 最优解可能在可行域内的任何一点达到 |
2.函数模型
| 线性规划 | 非线性规划 | |
| 模型标准型 | ||
| 函数名 | linprog | fmincon |
| 函数用法 |
|
|
参数含义:
| linprog | fmincon | ||
| f | 目标函数系数向量(列向量) | fun | 把目标函数定义成一个单独的函数文件(min) |
| A | 不等式约束矩阵(左侧系数) | x0 | 决策变量的初始值 |
| b | 不等式约束右侧常数向量 | A,b | 线性约束不等式变量系数矩阵和常数项矩阵(左侧系数和右侧向量,支持 |
| Aeq | 等式约束矩阵(Aeq),空表示无等式约束 | Aeq,beq | 线性约束等式变量系数矩阵和常数项矩阵(左侧系数和右侧向量) |
| beq | 等式约束右侧常数向量(beq),空表示无等式约束 | lb,ub | 决策变量的最小与最大取值(变量上下界) |
| lb | 变量下界(lower bound) | nonlcon | 非线性约束(包括不等式与等式) |
| ub | 变量上界(upper bound) | option | 求解非线性规划使用的方法 |
最不同的就是下面几个点:
| x0 | x0是初始值,这个选取比较重要,非线性规划算的是局部最优解,是在这个初始值下的最优解 1.可以给定不同初始值,在所有解里面得到最优解 2.先用蒙特卡罗模拟,找到一个蒙特卡罗解,然后把这个解作为初始值来求最优解 |
| option | 有5个算法可以选择 1.interior-point 2.sqp (Sequential Quadratic Programming) 3.sqp-legacy 4.active-set 5.trust-region-reflective 选择建议
|
| 目标函数 | 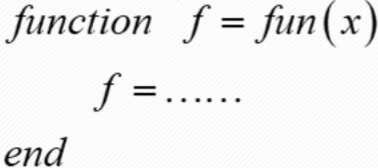 要写一个独立的脚本存目标函数 要写一个独立的脚本存目标函数 |
| nonlcon |  要写一个独立的脚本存非线性约束 要写一个独立的脚本存非线性约束 |
| 决策变量 | |
若不存在某种约束,可以用 [ ] 代替 若后面全都是 [ ] ,且option是默认,后面的 [ ] 可以不写 | |
这里另外提一句,这个公式不是特别好套用,尤其是存在而且有i,j之类的,感觉最好的办法是写出所有的xij按照行和列排,然后前面的系数提出来就是系数矩阵,尤其是不要忘记了前面是0系数的因素
比如这个![]() 如何写系数矩阵
如何写系数矩阵
有12个参数
矩阵全写出来
j=1
j=2
看似矩阵写作
实际上应该补0
应该写作