数据结构 排序(2)---选择排序
在上篇文章中,小编主要讲了第一类排序方法—插入排序,包括直接插入排序和希尔排序。今天小
编将会围绕第二类排序方法—选择排序展开讲述。
1. 直接选择排序
1.1 概念
直接选择排序是一种简单直观的排序算法,属于比较类排序。它的核心逻辑是“选最值、放到位”——通过不断从待排序元素里选出“最小(或最大)”的元素,放到合适位置,逐步完成排序。
你可以把它想象成“整理扑克牌”:每次从一堆打乱的牌里挑出最小的,放到最前面;再从剩下的牌里挑最小的,放到前一堆的后面……直到所有牌排好序。
1.2 基本思想
直接选择排序的基本思想 : 每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
- 把数组分成**“已排序区”和“未排序区”** 。初始时,已排序区为空,未排序区是整个数组;
- 每一轮,在未排序区里找“最小(或最大)”元素,和未排序区的第一个元素交换位置,把它“挪”到已排序区末尾;
- 重复这个过程,直到未排序区只剩1个元素(自然有序)。
1.3 代码实现
void SelectSort(int* arr, int n)
{int begin = 0, end = n - 1;while (begin < end){int maxi = begin;int mini = begin;for (int i = begin + 1;i <= end;i++){if (arr[i] < arr[mini]){mini = i;}if (arr[i] > arr[maxi]){maxi = i;}}//mini begin//maxi endif (maxi == begin){maxi = mini;}Swap(&arr[mini], &arr[begin]);Swap(&arr[maxi], &arr[end]);begin++;end--;}
}以下逐行详细解释这段直接选择排序代码的参数、变量含义,以及循环和逻辑的关系:
1. 函数定义与参数
void SelectSort(int* arr, int n)- void :函数无返回值,专注完成排序操作。
- int* arr :指向待排序数组的指针,通过它操作数组元素。
- int n :数组的元素个数,用于控制排序范围。
2. 变量初始化
int begin = 0, end = n - 1;- begin :标记当前未排序区间的起始位置,初始为数组第一个元素(下标 0 )。
- end :标记当前未排序区间的结束位置,初始为数组最后一个元素(下标 n-1 )。
- 逻辑: [begin, end] 构成当前轮次要处理的“未排序区间” ,每轮排序后 begin++ 、 end-- ,逐步缩小未排序区间。
3. 外层循环:控制排序轮次
while (begin < end)- 作用:只要 begin 小于 end,说明未排序区间至少有 2 个元素,需要继续排序。
- 结束条件:当 begin == end 时,未排序区间只剩 1 个元素(已自然有序),排序结束。
4. 内层循环前的变量
int maxi = begin; int mini = begin;- maxi :记录当前未排序区间内最大值的下标,初始假设起始位置 begin 是最大值位置。
- mini :记录当前未排序区间内最小值的下标,初始假设起始位置 begin 是最小值位置。
5. 内层循环:找最大、最小值下标
for (int i = begin + 1; i <= end; i++)- i :循环变量,从 begin + 1 开始遍历到 end (因为 begin 位置已初始化为 maxi 、 mini 对比基准 )。
- 循环逻辑:逐个对比 arr[i] 与当前 arr[mini] 、 arr[maxi] ,更新最值下标。
6. 找最小值下标
if (arr[i] < arr[mini]) {mini = i; }- 若当前元素 arr[i] 比之前记录的最小值 arr[mini] 还小,更新 mini 为 i (记录新的最小值下标 )。
7. 找最大值下标
if (arr[i] > arr[maxi]) {maxi = i; }- 若当前元素 arr[i] 比之前记录的最大值 arr[maxi] 还大,更新 maxi 为 i (记录新的最大值下标 )。
8. 特殊情况处理:交换位置冲突
if (maxi == begin) {maxi = mini; }- 场景:如果最大值原本就在 begin 位置(比如初始时 arr[begin] 是最大值 ),但后续交换最小值时( Swap(&arr[mini], &arr[begin]) ),会把 begin 位置的元素换掉。
- 作用:提前修正 maxi ,避免交换后找不到原来的最大值下标。
9. 交换操作:将最值放到目标位置
Swap(&arr[mini], &arr[begin]);- 作用:通过自定义的 Swap 函数(需实现交换两个元素值 ),把找到的最小值 arr[mini] 交换到 begin 位置,扩充已排序区间的起始部分。
把最小值放到未排序区间的起始,把最大值放到未排序区间的结束
10. 交换函数
Swap(&arr[maxi], &arr[end]);- 作用:把找到的最大值 arr[maxi] 交换到 end 位置,扩充已排序区间的结束部分。
11. 缩小未排序区间
begin++; end--;- 逻辑:每轮排序后, begin 后移、 end 前移,未排序区间 [begin, end] 缩小,下一轮处理更短的区间。
完整流程总结:
1. 初始化区间: begin=0 、 end=n-1 ,确定最开始的未排序区间是整个数组。
2. 内层循环找最值:在 [begin, end] 里遍历,找到最小值下标 mini 、最大值下标 maxi 。
3. 处理交换冲突:防止最大值在 begin 位置时,被最小值交换“覆盖”,提前修正 maxi 。
4. 交换最值到位:最小值放 begin ,最大值放 end ,固定这两个位置为“已排序”。
5. 缩小区间: begin++ 、 end-- ,进入下一轮排序,直到 begin >= end 结束。
这样,每一轮都会让未排序区间的最左(最小)和最右(最大) 元素归位,逐步把数组“挤”成有序,这就是直接选择排序(同时找最大、最小优化版) 的完整逻辑 。
1.4 代码运行流程实例
小编仍以数组 [5, 3, 4, 6, 2] 为例,用直接选择排序一步步实现升序(从小到大)排列。
第一轮:
1. 初始化:
- 函数参数: arr 指向数组 [5, 3, 4, 6, 2] , n = 5 。
- 初始化变量: begin = 0 , end = 4 , maxi = 0 , mini = 0 。2. 内层循环找最值下标:
- i 从 begin + 1 = 1 开始,到 end = 4 结束。
- 当 i = 1 时:
- arr[1] = 3 , arr[mini] = arr[0] = 5 ,因为 3 < 5 ,所以 mini = 1 。
- arr[1] = 3 , arr[maxi] = arr[0] = 5 ,因为 3 < 5 , maxi 不变,仍为 0 。
- 当 i = 2 时:
- arr[2] = 4 , arr[mini] = arr[1] = 3 ,因为 4 > 3 , mini 不变。
- arr[2] = 4 , arr[maxi] = arr[0] = 5 ,因为 4 < 5 , maxi 不变。
- 当 i = 3 时:
- arr[3] = 6 , arr[mini] = arr[1] = 3 ,因为 6 > 3 , mini 不变。
- arr[3] = 6 , arr[maxi] = arr[0] = 5 ,因为 6 > 5 ,所以 maxi = 3 。
- 当 i = 4 时:
- arr[4] = 2 , arr[mini] = arr[1] = 3 ,因为 2 < 3 ,所以 mini = 4 。
- arr[4] = 2 , arr[maxi] = arr[3] = 6 ,因为 2 < 6 , maxi 不变。3. 特殊情况处理:
- 此时 maxi = 3 , begin = 0 , maxi != begin ,不需要进行特殊处理。4. 交换操作:
- 交换最小值到未排序区间起始位置: Swap(&arr[mini], &arr[begin]) ,即交换 arr[4] 和 arr[0] ,数组变为 [2, 3, 4, 6, 5] 。9
- 交换最大值到未排序区间结束位置: Swap(&arr[maxi], &arr[end]) ,即交换 arr[3] 和 arr[4] ,数组变为 [2, 3, 4, 5, 6] 。5. 缩小未排序区间:
- begin++ 变为 1 , end-- 变为 3 ,此时未排序区间变为 [1, 3] 。
第二轮:
1. 内层循环找最值下标:
- i 从 begin + 1 = 2 开始,到 end = 3 结束。
- 当 i = 2 时:
- arr[2] = 4 , arr[mini] = arr[1] = 3 ,因为 4 > 3 , mini 不变。
- arr[2] = 4 , arr[maxi] = arr[1] = 3 ,因为 4 > 3 ,所以 maxi = 2 。
- 当 i = 3 时:
- arr[3] = 5 , arr[mini] = arr[1] = 3 ,因为 5 > 3 , mini 不变。
- arr[3] = 5 , arr[maxi] = arr[2] = 4 ,因为 5 > 4 ,所以 maxi = 3 。2. 特殊情况处理:
- 此时 maxi = 3 , begin = 1 , maxi != begin ,不需要进行特殊处理。-3. 交换操作:
- 交换最小值到未排序区间起始位置: Swap(&arr[mini], &arr[begin]) , mini = 1 , begin = 1 ,不需要交换。
- 交换最大值到未排序区间结束位置: Swap(&arr[maxi], &arr[end]) ,即交换 arr[3] 和 arr[3] ,也不需要交换,数组保持 [2, 3, 4, 5, 6] 。4. 缩小未排序区间:
- begin++ 变为 2 , end-- 变为 2 ,此时未排序区间变为 [2, 2] 。
第三轮:
- 此时 begin = 2 , end = 2 ,不满足 while (begin < end) 的条件,外层循环结束,排序完成,最终得到有序数组 [2, 3, 4, 5, 6] 。
通过以上步骤,每一轮都能确定未排序区间的最小值和最大值,并将它们放到合适的位置,逐步使整个数组有序。
1.5 降序
上述方法时队数组进行了升序,如果要实现降序呢,只需修改判断“最大值”和“最小值”的条件,同时交换逻辑也对应调整(把最大值放左边,最小值放右边)。具体改法如下:
降序修改的核心代码(仅改3处)原升序代码中,判断“谁是更小/更大”的符号和交换目标位置需要反转:void SelectSortDesc(int* arr, int n) // 函数名可加Desc区分降序
{int begin = 0, end = n - 1;while (begin < end){int maxi = begin; // 记录最大值下标(降序中,最大值要放左边)int mini = begin; // 记录最小值下标(降序中,最小值要放右边)for (int i = begin + 1; i <= end; i++){// 1. 找最大值:修改判断符号(> 改为 <,因为要找更大的)if (arr[i] > arr[maxi]) // 原升序是找最小值用 <,这里找最大值用 >{maxi = i;}// 2. 找最小值:修改判断符号(< 改为 >,因为要找更小的)if (arr[i] < arr[mini]) // 原升序是找最大值用 >,这里找最小值用 <{mini = i;}}// 特殊情况处理:若最小值在begin位置,交换最大值后会被覆盖,需修正miniif (mini == begin) // 原升序是判断maxi == begin,这里反转判断mini{mini = maxi;}// 3. 交换目标位置反转:最大值放begin(左),最小值放end(右)Swap(&arr[maxi], &arr[begin]); // 原升序是交换最小值到begin,这里换最大值Swap(&arr[mini], &arr[end]); // 原升序是交换最大值到end,这里换最小值begin++;end--;}
}总结 : 降序只需3处修改:
- - 找最大值的判断符号( > 保留,原升序找最小值用 < );
- - 找最小值的判断符号( < 保留,原升序找最大值用 > );
- - 交换目标和特殊情况判断的变量(maxi 和 mini 互换角色)。
核心逻辑不变,只是“最值的目标位置”和“判断标准”反转了。
1.6 复杂度
1. 时间复杂度
所有情况均为 O(n²)(n 为数组长度),具体分析:
1. 外层循环:控制排序轮次,从 begin=0 到 begin < end ,共执行约 n/2 轮(每轮缩小 2 个元素的区间)。
2. 内层循环:每轮在未排序区间 [begin, end] 中遍历找最值,第 1 轮遍历 n 个元素,第 2 轮遍历 n-2 个元素,……,最后一轮遍历 2 个元素。
总遍历次数约为 n + (n-2) + (n-4) + ... + 2 ,这是一个等差数列,求和结果约为 n²/2 ,属于 O(n²) 级别。
无论数组是否有序(比如完全有序、完全倒序、随机无序),都需要完整执行所有轮次的遍历找最值,因此最好、最坏、平均时间复杂度都是 O(n²)。
2. 空间复杂度
O(1),原因:
排序过程中仅使用了固定数量的临时变量( begin 、 end 、 maxi 、 mini 、 i 等),这些变量的内存占用不随数组长度 n 变化,不需要额外开辟与 n 相关的存储空间(如额外数组),属于原地排序算法。
- 时间复杂度:O(n²)(固定,不受数据分布影响)。
- 空间复杂度:O(1)(原地排序,仅用常数空间)。
这也是选择排序的特点:逻辑简单但效率较低,适合数据量小的场景。
2. 堆排序
选择排序除了直接选择排序外,还包括堆排序。因为堆排序小编在之前的关于堆的文章中有过详细解释,所以这里便不再过多赘述了。如果有问题的小伙伴可以去看一下小编之前的文章。现在小编将关于堆排序的代码留给大家。
//交换函数(下面会用到)
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}
//向下调整算法
void AdjustDown(int* arr, int parent, int n)
{int child = parent * 2 + 1;//左孩子while (child < n){// 大堆 : <// 小堆 : >if (child + 1 < n && arr[child] < arr[child + 1]){child++;}//大堆 : >//小堆 : <if (arr[child] > arr[parent]){//调整Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
//堆排序
//升序 : 建大堆
//降序 : 减小堆
void HeapSort(int* arr, int n)
{//建堆 : 向下调整算法建堆for (int i = (n - 1 - 1) / 2;i >= 0;i--){AdjustDown(arr, i, n);}int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, 0, end);end--;}
}
在之前小编在讲有关堆的文章中,小编对堆排序的代码实现,函数的逻辑以及复杂度都进行了详细的讲解,有兴趣的可以去看一下。
3. 总结
最后小编对上面的两个排序在编译器中进行一下测试:
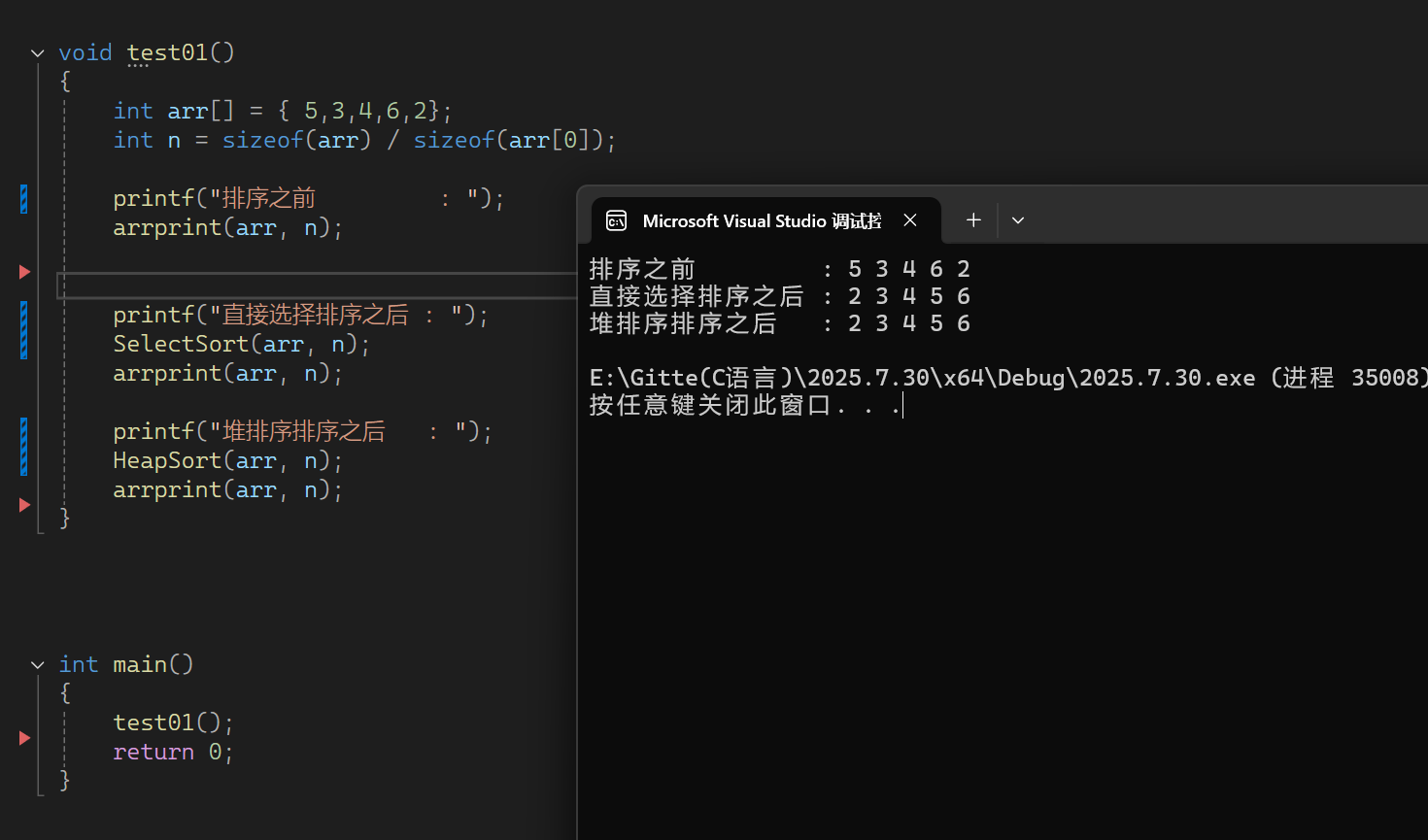
由上面的调试结果可知,代码的内容以及测试结果都是正确的。
总结:
选择排序是一种基础排序算法,核心逻辑是“选最值,放到位” :每轮从待排序元素里选最小(或最大)的,放到对应位置,逐步完成排序。包含 直接选择排序 和 堆排序 这两种常见实现:
- 直接选择排序:简单直观,逐轮遍历找最值交换,时间复杂度稳定 O(n²),适合小数据;
- 堆排序:借助堆结构高效选最值,时间复杂度优化到 O(nlogn),更适合大数据。
本质都是通过“选择最值”来排序,堆排序是对直接选择排序的效率优化。
以上内容便是关于第二类排序—选择排序的主要内容,大家可以自己再实现一下。最后感谢大家的
观看!
