编译原理第四到五章(知识点学习/期末复习/笔试/面试)
第四章 语法分析(自顶向下分析)
自顶向下的分析(Top-Down Parsing)
从分析树的顶部(根节点)向底部(叶节点)方向构造分析树
可以看成是从文法开始符号S推导出词串w的过程
例子:(开始符号默认产生式第一条左部)
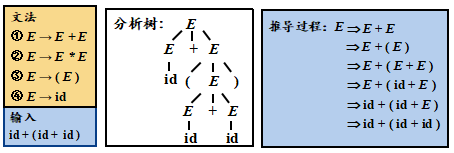
每一步推导中,都需要做两个选择
- 替换当前句型中的哪个非终结符
- 用该非终结符的哪个候选式进行替换
最左推导(Left-most Derivation)
在最左推导中,总是选择每个句型的最左非终结符进行替换
如果![]() ,则称α是当前文法的最左句型(left-sentential form)
,则称α是当前文法的最左句型(left-sentential form)
例子:
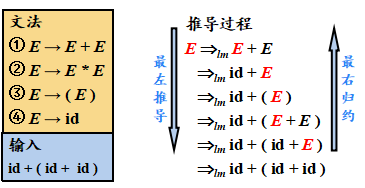
最右推导(Right-most Derivation)
在最右推导中,总是选择每个句型的最右非终结符进行替换
在自底向上的分析中,总是采用最左归约的方式,因此把最左归约称为规范归约,而最右推导相应地称为规范推导。
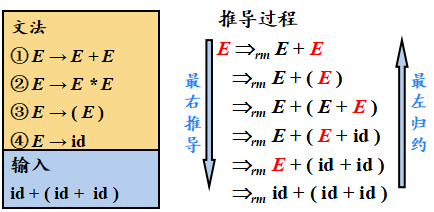
最左推导和最右推导的唯一性
最左推导和最右推导具有唯一性。
自顶向下的语法分析采用最左推导方式
- 总是选择每个句型的最左非终结符进行替换
- 根据输入流中的下一个终结符,选择最左非终结符的一个候选式
例子:
文法:
① E → T E’
② E’→ + T E’|ε
③ T → F T’
④ T’→ * F T’|ε
⑤ F → ( E )|id
输入: id + id * id
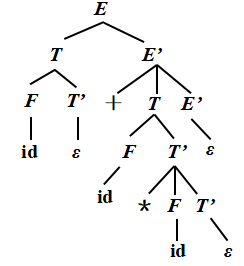
自顶向下语法分析的通用形式
递归下降分析 (Recursive-Descent Parsing)
- 由一组过程组成,每个过程对应一个非终结符
- 从文法开始符号S对应的过程开始,递归调用文法中其它非终结符对应的过程。如果S对应的过程体恰好扫描了整个输入串,则成功完成语法分析
void A( ) {
选择一个A产生式, A →X1 X2 … Xk ;
for ( i = 1 to k ) {
if ( Xi是一个非终结符号)
调用过程 Xi ( ) ;
else if ( Xi 等于当前的输入符号a)
读入下一个输入符号;
else /* 发生了一个错误 */ ;
}
}
可能需要回溯(backtracking),导致效率较低
预测分析 (Predictive Parsing)
预测分析是递归下降分析技术的一个特例,通过在输入中向前看固定个数(通常是一个)符号来选择正确的A-产生式。
可以对某些文法构造出向前看k个输入符号的预测分析器,该类文法有时也称为LL(k) 文法类 (scanning input from Left to right, producing a Leftmost derivation) 预测分析不需要回溯,是一种确定的自顶向下分析方法。
预测分析不需要回溯,是一种确定的自顶向下分析方法。
文法转换
问题1:L(G)中某个句子存在两棵以上分析树,二义性
文法G:E → E + E | E * E | (E) | id
输入语句:id + id * id
文法改造,引入新的语法变量(问题1)
文法G':E → E + T | T ;T → T * F | F ;F → (E) | id
问题2:同一非终结符的多个候选式存在共同前缀,将导致回溯现象
文法G:S → aAd | aBe ;A → c;B → b
输入: a b c
提取左公因子(Left Factoring )(问题2)
文法G':S → a S';S' → Ad | Be ;A → c ;B → b
通过改写产生式来推迟决定,等读入了足够多的输入,获得足够信息后再做出正确的选择。
提取左公因子算法
输入:文法G
输出:等价的提取了左公因子的文法
方法:
对于每个非终结符A,找出它的两个或多个选项之间的最长公共前缀α。如果α ≠ ε, 即存在一个非平凡的( nontrivial )公共前缀,那么将所有A-产生式
- A → α β1 | α β2 | … | α βn | γ1 | γ2 | … | γm
替换为
- A → α A' | γ1 | γ2 | … | γm
- A' → β1 | β2 | … | βn
其中, γi 表示所有不以α开头的产生式体; A‘是一个新的非终结符。不断应用该 转换,直到每个非终结符的任意两个产生式体都没有公共前缀为止。
问题3:左递归文法会使递归下降分析器陷入无限循环
含有A→Aα形式产生式的文法称为是直接左递归的(immediate left recursive)。
如果一个文法中有一个非终结符A使得对某个串α存在一个推导A→+Aα ,则该文法就是左递归的
经过两步或两步以上推导产生的左递归称为是间接左递归的
例子:
文法G:
E → E + T | E – T | T
T → T * F | T / F | F
F → ( E ) | id
输入 :id + id * id
E → E + T→E + T+ T→E + T+ T+ T→.......
消除直接左递归(问题3)
A → Aα | β (α≠ ε, β不以A开头) r=βα*
改为:
A → β A′
A′ → α A′|ε
例子
E → E + T|T
T → T * F|F
F → ( E )|id
改为:
E → T E′
E′ → + TE′|ε
T → FT ′
T ′→ * FT ′|ε
F → ( E )|id
消除直接左递归的一般形式
A → A α1 | A α2 | … | A αn | β1 | β2 | … | βm (αi ≠ ε, βj不以A开头)
改为:
A → β1 A′ | β2 A′ | … | βm A′
A′ → α1 A′ | α2 A′ | … | αn A′ | ε
消除左递归是要付出代价的——引进了一些非终结符和ε产生式
消除间接左递归
例子:S → A a | b ; A → S d | ε
(S → A a→ Sda 是左递归)
将S的定义代入A-产生式,得: A → A a d | b d | ε
消除A-产生式的直接左递归,得:A→ b d A’ | A’ ;A’→a dA’ | ε
消除左递归算法
输入:不含循环推导(即形如A →+ A的推导)和ε-产生式的文法G
输出:等价的无左递归文法
方法:
按照某个顺序将非终结符号排序为A1,A2,… ,An .
for (i ∈ 1 to n ) {
for ( j ∈ 1 to i -1 ) {
将每个形如Ai → Aj γ的产生式替换为产生式组 Ai → δ1 γ∣δ2 γ∣…∣δk γ ,
其中Aj → δ1∣δ2∣… ∣δk ,是所有的Aj 产生式
}
消除Ai 产生式之间的立即左递归
}
LL(1) 文法
什么样的文法适合预测分析法
预测分析法的工作过程
- 从文法开始符号出发,在每一步推导过程中根据当前句型的最左非终结符A和当前输入符号a,选择正确的A-产生式。
- 为保证分析的确定性,选出的候选式必须是唯一的。
A → aB | B ;B → Cb ;C → a
串首终结符集
串首终结符,串首第一个符号,并且是终结符。简称首终结符。
给定一个文法符号串α, α的串首终结符集FIRST(α)被定义为可以从α推导出的所有串首终结符构成的集合。如果α →* ε,那么ε也在FIRST(α)中
- 对于 任意α∈(VT∪V N)+, FIRST(α)={ a | α →* aβ,a∈ VT,β∈(V T∪ V N)*};
- 如果 α →* ε,那么 ε∈FIRST(α)
对G的任意两个具有相同左部的产生式A → α | β (假设α,β非空)
- 如果FIRST(α)∩FIRST(β) = Φ,则可以对G进行自顶向下分析
如果
A → α | β两个产生式的 FIRST 集合没有交集,那么在分析字符串时,只需要看串首字符,就能唯一确定用哪个产生式。这种语法就能用预测分析(例如 LL(1))来处理,也就是自顶向下分析是可行的
比如:
A → aB | bC
FIRST(aB) = {a}
FIRST(bC) = {b}
交集是空集(a ≠ b)
这就好!
如果α →* ε or β →* ε,那么我们要引入FOLLOW集的概念
如果 α 或 β 能够推导出 ε(空串),那就会出现一个新问题:
此时,字符串可能是空的,我们无法通过串首终结符唯一判断要用哪个产生式了。
举个例子:
A → aB | ε
FIRST(aB) = {a}
FIRST(ε) = {ε}
能看出,如果接下来的字符不是
a,我们需要知道“是否可以用 ε”。这时候就需要用 FOLLOW 集,也就是判断在什么情况下可以使用 ε。
例子:
文法:S → aBC ;B → bC ;B → dB; B → ε ;C → c | a
输入.:a d a
推导:S → aBC→adBC→adC→ada
可以紧跟 B后面出现的终结符:c、a
如果当前某非终结符A与当前输入符a不匹配时,若a可以出现在 A后面,则可以使用产生式 A→ε.
当前我们要分析一个非终结符 A,如果它的 FIRST 集合和当前输入符号 a 没有交集(也就是说它不能“吃掉”这个 a),但这个 a 可以在 A 的 FOLLOW 集里(也就是 A 后面可以跟 a),那我们就可以考虑使用
A → ε。
非终结符的后继符号集
非终结符A的后继符号集
可能在某个句型中紧跟在A后边的终结符a的集合,记为FOLLOW(A)
FOLLOW(A)={a| S →* αAaβ, a∈VT,α,β∈(VT∪VN)*}
如果 A是某个句型的的最右符号, 则将结束符“$”添加到FOLLOW(A)中
对G的任意两个具有相同左部的产生式A → α | β
如果 β →* ε,则FIRST (α)∩FOLLOW(A) =Φ;
如果 α →* ε,则FIRST (β)∩FOLLOW(A) =Φ;
在某些产生式右边能变成 ε(空串)的情况下,我们要确保另一个右部的 FIRST 集合和 A 的 FOLLOW 集合不能冲突,否则分析器就分不清要选哪条产生式。
给出文法:
S → A a
A → aB | ε
输入的串是
a
FIRST(α) = {a}
FOLLOW(A) = {a}
假如用 LL(1) 预测分析表,遇到当前输入符号
a:
你一方面觉得应该用
A → aB,因为 FIRST(α) 有 a;另一方面你又觉得可以用
A → ε,因为当前符号 a 出现在 FOLLOW(A) 中,也满足 A → ε 的触发条件。产生冲突,无法预测
如果 β 可以推导出 ε,为了避免冲突,就必须保证:当前输入符号不能既在 FIRST(α) 中,又在 FOLLOW(A) 中。反过来也一样:如果 α ⇒* ε,则必须确保 FIRST(β) ∩ FOLLOW(A) = ∅。
LL(1)文法
文法G是LL(1)的,当且仅当G的任意两个具有相同左部的产生式A → α | β 满足下面的条件:
- 若α 和β都不为空,则FIRST(α)∩FIRST(β) = Φ
- α 和β至多有一个能推导出ε 且
- 如果 β ⇒* ε,则FIRST (α)∩FOLLOW(A) =Φ;
- 如果 α ⇒ * ε,则FIRST (β)∩FOLLOW(A) =Φ;
同一非终结符的各个产生式互不冲突
- 第一个“L”表示从左向右扫描输入
- 第二个“L”表示产生最左推导
- “1”表示在每一步中只需要向前看一个输入符号来决定语法分析动作
FIRST集和FOLLOW集的计算
计算文法符号X的FIRST(X )
- FIRST ( X ):可以从X推导出的所有串首终结符构成的集合
- 如果 X ⇒* ε,那么 ε∈FIRST ( X )
算法
计算FIRST(X) (from the dragon book)
输入:G=(VT , VN , P , S ),X∈(VT ∪VN);
输出:FIRST(X);
步骤:

例子:
① E → TE' ② E' → +TE' |ε ③ T → FT ' ④ T' → *FT ' |ε ⑤ F → (E)|id
FIRST ( E ) = { ( , id }
FIRST ( E' ) = { + , ε }
FIRST ( T ) = { ( , id }
FIRST ( T' ) = { * , ε }
FIRST ( F ) = { ( , id }
计算串X1X2 …Xn的FIRST 集合
- 向FIRST(X1X2 …Xn)加入FIRST(X1)中所有的非ε符号
- 如果ε在FIRST(X1)中,再加入FIRST(X2)中的所有非ε符号;
- 如果ε在FIRST(X1)和FIRST(X2)中,再加入FIRST(X3)中的所有非ε符号,以此类推
- 最后,如果对所有的i,ε都在FIRST(Xi)中,那么将ε加入到FIRST(X1X2 …Xn) 中
计算非终结符A的FOLLOW(A)
FOLLOW(A):可能在某个句型中紧跟在A后边的终结符a的集合
FOLLOW(A)={a| S ⇒* αAaβ, a∈VT,α,β∈(VT∪VN)*}
$∈FOLLOW(S)
如果A是某个句型的的最右符号,则将结束符$添加到FOLLOW(A)中
算法
不断应用下列规则,直到没有新的终结符可以被加入到任何FOLLOW集合中为止
- 将$放入FOLLOW( S )中,其中S是开始符号,$是输入右端的结束标记
- 如果存在一个产生式A→αBβ,那么FIRST ( β )中除ε 之外的所有符号都在FOLLOW( B )中
- 如果存在一个产生式A→αB,或存在产生式A→αBβ且FIRST ( β ) 包含ε,那么 FOLLOW( A )中的所有符号都在FOLLOW( B )中
如果 B 出现在某条产生式的末尾,或者 B 后面能推出空串,那么 B 后面其实是“什么都没有”,那就说明 A 后面能出现的符号,也可以出现在 B 后面,所以要把 FOLLOW(A) 加到 FOLLOW(B) 中。
如果一个句型中
B是A的最后一部分(或者 B 后面的内容可以消失),那么当我们替换 A 为 B 的时候,B 就要承担 A 在句子里的“后续位置”,自然也要继承 A 的 FOLLOW 集。
例子:
① E → TE' ② E' → +TE' |ε ③ T → FT ' ④ T' → *FT ' |ε ⑤ F → (E)|id
FIRST ( E ) = { ( , id } FOLLOW ( E ) = { $ , ) }
FIRST ( E' ) = { + , ε } FOLLOW ( E' ) = { $ , ) }
FIRST ( T ) = { ( , id } FOLLOW ( T ) = { $ , ) , +}
FIRST ( T' ) = { * , ε } FOLLOW ( T' ) = { $, ) , +}
FIRST ( F ) = { ( , id } FOLLOW ( F ) = {$, ) , + , * }
构造预测分析表

产生式 | |
E | E→TE' |
E' | E'→+TE’ |
E'→ε | |
T | T→FT' |
T' | T'→*FT’ |
T'→ε | |
F | F→( E ) |
F→id |
X | FIRST( X ) | FOLLOW( X ) |
E | ( id | $ ) |
E ' | + ε | $ ) |
T | ( id | + ) $ |
T ' | * ε | + ) $ |
F | ( id | * + ) $ |
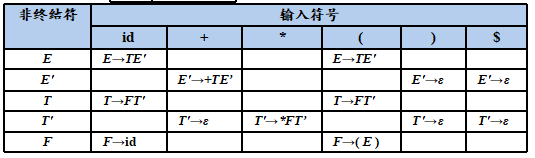
预测分析表的填法原则:
对于每个产生式 A → α,执行以下步骤:
1. 对于所有 a ∈ FIRST(α),填 M[A, a] = A → α
2. 如果 ε ∈ FIRST(α),则对于所有 b ∈ FOLLOW(A),填 M[A, b] = A → α
3. FIRST(α) 中不包括 ε 的时候,不考虑 FOLLOW 集
第一行:E
产生式是 E → T E',FIRST(T) 是 ( id
所以:
M[E, id] = E → T E'M[E, (] = E → T E'
第二行:E'
有两个产生式:
E' → + T E':FIRST 是+,所以:M[E', +] = E' → + T E'
E' → ε:因为 ε ∈ FIRST(E'),根据规则 2,填在 FOLLOW(E') 中的每个符号,即)和$M[E', )] = E' → εM[E', $] = E' → ε
第三行:T
产生式是 T → F T',FIRST(F) 是 ( id
M[T, id] = T → F T'M[T, (] = T → F T'
第四行:T'
两个产生式:
T' → * F T':FIRST 是*M[T', *] = T' → * F T'
T' → ε:因为 ε ∈ FIRST(T'),要填到 FOLLOW(T') 里,也就是+ ) $M[T', +] = T' → εM[T', )] = T' → εM[T', $] = T' → ε
第五行:F
两个产生式:
F → id:FIRST 是idM[F, id] = F → id
F → ( E ):FIRST 是(M[F, (] = F → ( E )
LL(1)文法的分析方法-非递归的预测分析法
非递归的预测分析法
非递归的预测分析不需要为每个非终结符编写递归下降过程,而是根据预测分析表构造一个自动机,也叫表驱动的预测分析
下推自动机 (Push Down Automata, PDA)
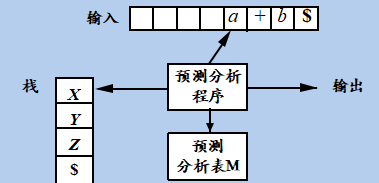
表驱动的预测分析法
输入:一个串w和文法G的分析表 M
输出:如果w在L(G )中,输出w的最左推导;否则给出错误指示
方法:最初,语法分析器的格局如下:输入缓冲区中是w$,G的开始符号位于栈顶,其下面是$。下面的程序使用预测分析表M生成了处理这个输入的预测分析过程
设置ip使它指向w的第一个符号,其中ip 是输入指针;
令X=栈顶符号;
while ( X ≠ $ ){ /* 栈非空 */
if ( X 等于ip所指向的符号a) 执行栈的弹出操作,将ip向前移动一个位置;
else if ( X是一个终结符号) error ( ) ;
else if ( M[X,a]是一个报错条目) error ( ) ;
else if ( M[X,a] = X →Y1Y2 … Yk ){
输出产生式 X →Y1Y2 … Yk ;
弹出栈顶符号;
将Yk,Yk-1 …,Y1 压入栈中,其中Y1位于栈顶。
}
令X=栈顶符号
}
例子:

如果w是至今为止已经匹配完成的输入部分,那么栈中保存的文法符号序列α满足 S ⇒*lm wα

预测分析法实现步骤
1)构造文法
2)改造文法:消除二义性、消除左递归、消除回溯
3)求每个变量的FIRST集和FOLLOW集
4)检查是不是 LL(1) 文法。若是,构造预测分析表
5)对于递归的预测分析,根据预测分析表为每一个非终结符编写一个过程;对于非递归的预测分析,实现表驱动的预测分析算法
LL(1)文法的分析方法-递归的预测分析法
递归的预测分析法
递归的预测分析法是指:在递归下降分析中,根据预测分析表进行产生式的选择
根据每个非终结符的产生式和LL(1)文法的预测分析表,为每个非终结符编写对应的过程
什么是“递归预测分析法”?
它就是为每一个非终结符号写一个“函数”,这个函数根据输入的当前单词(TOKEN)和预测分析表决定:
应该用哪条产生式?
用了这条产生式后,要不要调用别的函数(即处理别的非终结符)?
要不要匹配终结符?
void A( ) {
选择一个A产生式, A →X1 X2 … Xk ;
for ( i = 1 to k ) {
if ( Xi是一个非终结符号)
调用过程 Xi ( ) ;
else if ( Xi 等于当前的输入符号a)
读入下一个输入符号;
else /* 发生了一个错误 */ ;
}
}
例子
(1) <PROGRAM> → program <DECLIST> :<TYPE> ; <STLIST> end
(2) <DECLIST> → id <DECLISTN>
(3) <DECLISTN> → , id <DECLISTN>
(4) <DECLISTN> → ε
(5) <STLIST> → s <STLISTN>
(6) <STLISTN> → ; s <STLISTN>
(7) <STLISTN> → ε
(8) <TYPE> → real
(9) <TYPE> → int
这个文法的意思是:
一个程序以关键字
program开头然后是若干变量声明(由
<DECLIST>处理)然后是冒号
:和类型(real 或 int)然后分号
;和语句列表最后是
end
program DESCENT;
begin
GETNEXT(TOKEN);
PROGRAM(TOKEN);
GETNEXT(TOKEN);
if TOKEN≠’$’ then ERROR;
end
输入串:program id , id : int ; s ; s end
为每个非终结符,比如 <PROGRAM>、<DECLIST>,写一个过程(函数)来处理它。
我们来写 PROGRAM() 函数(也就是处理 <PROGRAM>)
根据第(1)条产生式:<PROGRAM> → program <DECLIST> : <TYPE> ; <STLIST> end
写的 PROGRAM() 伪代码应该是这样:
void PROGRAM() {
if (TOKEN == "program") {
GETNEXT(); // 读下一个单词
DECLIST(); // 处理 <DECLIST>
if (TOKEN == ":") {
GETNEXT();
TYPE(); // 处理 <TYPE>
if (TOKEN == ";") {
GETNEXT();
STLIST(); // 处理 <STLIST>
if (TOKEN == "end") {
GETNEXT(); // 结束
} else ERROR;
} else ERROR;
} else ERROR;
} else ERROR;
}
根据第(2)条产生式:<DECLIST> → id <DECLISTN>
写的 DECLIST() 伪代码应该是这样:
procedure DECLIST(TOKEN);
begin
if TOKEN≠’id’ then ERROR;
GETNEXT(TOKEN);
DECLISTN(TOKEN);
end
根据第(3)和第(4)条产生式:<DECLISTN> → , id <DECLISTN>;) <DECLISTN> → ε
写的 DECLISTN() 伪代码应该是这样:
procedure DECLISTN(TOKEN);
begin
if TOKEN =‘,’ then
begin
GETNEXT(TOKEN);
if TOKEN≠’id’ then ERROR;
GETNEXT(TOKEN);
DECLISTN(TOKEN);
end
else if TOKEN≠’:’ then ERROR;
end
根据第(5)条产生式: <STLIST> → s <STLISTN>
写的 STLIST() 伪代码应该是这样:
procedure STLIST(TOKEN);
begin
if TOKEN≠’s’ then ERROR;
GETNEXT(TOKEN);
STLISTN(TOKEN);
end
根据第(6)和(7)条产生式: <STLISTN> → ; s <STLISTN>;<STLISTN> → ε
写的 STLISTN() 伪代码应该是这样:
procedure STLISTN(TOKEN);
begin
if TOKEN =‘;’ then
begin
GETNEXT(TOKEN);
if TOKEN≠’s’ then ERROR;
GETNEXT(TOKEN);
STLISTN(TOKEN);
end
else if TOKEN≠’end’ then ERROR;
end
根据第(8)和(9)条产生式: <TYPE> → real;<TYPE> → int
写的 TYPE() 伪代码应该是这样:
procedure TYPE(TOKEN);
begin
if TOKEN≠’real’ and TOKEN≠’int’
then ERROR;
end
递归的预测分析法vs.非递归的预测分析法
递归的预测分析法 | 非递归的预测分析法 | |
程序规模 | 程序规模较大, 不需载入分析表 | 主控程序规模较小, 需载入分析表(表较小) |
直观性 | 较好 | 较差 |
效率 | 较低 | 分析时间大约正比于待分析程序的长度 |
自动生成 | 较难 | 较易 |
预测分析中的错误处理
预测分析中的错误检测
两种情况下可以检测到错误
- 栈顶的终结符和当前输入符号不匹配
- 栈顶非终结符与当前输入符号在预测分析表对应项中的信息为空
预测分析中的错误恢复
恐慌模式
- 忽略输入中的一些符号,直到输入中出现由设计者选定的同步词法单元(synchronizing token)集合中的某个词法单元
- 其效果依赖于同步集合的选取。集合的选取应该使得语法分析器能从实际遇到的错误中快速恢复。 例如可以把FOLLOW(A)中的所有终结符放入非终结符A的同步记号集合
- 如果终结符在栈顶而不能匹配,一个简单的办法就是弹出此终结符
例子:
Synch表示根据相应非终结符的FOLLOW集得到的同步词法单元
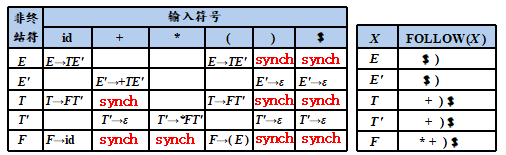
分析表的使用方法
- 如果M[A,a]是空,表示检测到错误,根据恐慌模式,忽略输入符号a
- 如果M[A,a]是synch,则弹出栈顶的非终结符A,试图继续分析后面的语法成分
- 如果栈顶的终结符和输入符号不匹配,则弹出栈顶的终结符

第五章 语法分析(自底向上的语法分析)
自底向上的语法分析
- 从分析树的底部(叶节点)向顶部(根节点)方向构造分析树
- 可以看成是将输入串w归约为文法开始符号S的过程
- 自顶向下的语法分析采用最左推导方式
- 自底向上的语法分析采用最左归约方式(反向构造最右推导)
- 自底向上语法分析的通用框架:移入-归约分析(Shift-Reduce Parsing)
移入-归约分析的工作过程
- 在对输入串的一次从左到右扫描过程中,语法分析器将零个或多个输入符号移入到栈的顶端,直到它可以对栈顶的一个文法符号串β进行归约为止
- 然后,它将β归约为某个产生式的左部
- 语法分析器不断地重复这个循环,直到它检测到一个语法错误,或者栈中包含了开始符号且输入缓冲区为空(当进入这样的格局时,语法分析器停止运行,并宣称成功完成了语法分析)为止
每次归约的符号串称为“句柄”
例子
文法: ① E → E+E ② E → E*E ③ E → (E) ④ E → id

栈内符号串 + 剩余输入 =“规范句型”
移入-归约分析器可采取的4种动作
- 移入:将下一个输入符号移到栈的顶端
- 归约:被归约的符号串的右端必然处于栈顶。语法分析器在栈中确定这个串的左端,并决定用哪个非终结符来替换这个串
- 接收:宣布语法分析过程成功完成
- 报错:发现一个语法错误,并调用错误恢复子例程
移入-归约分析中存在的问题
句柄:句型的最左直接短语
造成错误的原因: 错误地识别了句柄
例子:
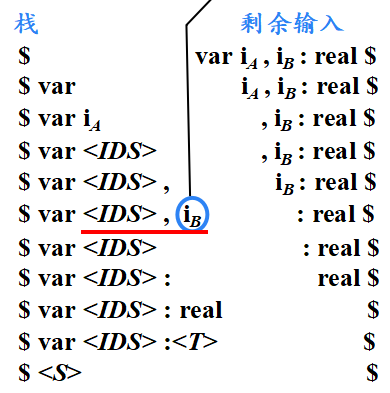
(1) <S>→var <IDS> : <T> (2) <IDS>→i (3) <IDS>→<IDS> , i (4) <T>→real | int
错误的例子(错误地识别了句柄):

iB直接被规约成<IDS>,不对的
<IDS>,iB可以被一起规约为<IDS>
正确应该是:
LR分析法概述
LR 分析法
LR文法(Knuth, 1963) 是最大的、可以构造出相应移入-归约句法分析器的文法类
- L: 对输入进行从左到右的扫描
- R: 反向构造出一个最右推导序列
LR(k)分析
- 需要向前查看k个输入符号的LR分析
- k = 0 和 k = 1 这两种情况具有实践意义
- 当省略(k)时,表示k =1
LR 分析法的基本原理
自底向上分析的关键问题是什么? 如何正确地识别句柄
句柄是逐步形成的,用“状态”表示句柄识别的进展程度
LR分析器基于这样一些状态来构造自动机进行句柄的识别
例子:S→bBB
移进状态:S→ ·bBB
待约状态:S→b·BB;S→bB·B
归约状态:S→bBB·
LR 分析器(自动机)的总体结构
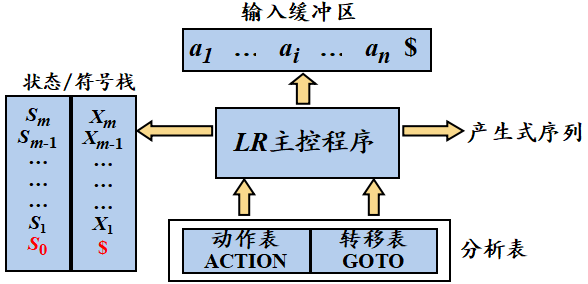
LR 分析表的结构
sn:将符号a、状态n 压入栈
rn:用第n个产生式进行归约
例子:
文法:① S→BB ② B→aB ③ B→b
状态 | ACTION | GOTO | |||
a | b | $ | S | B | |
0 | s3 | s4 | 1 | 2 | |
1 | acc | ||||
2 | s3 | s4 | 5 | ||
3 | s3 | s4 | 6 | ||
4 | r3 | r3 | r3 | ||
5 | r1 | r1 | r1 | ||
6 | r2 | r2 | r2 | ||
LR 分析器的工作过程
(s0-sm表状态)
初始化:
s0
$ a1a2…an $
一般情况下:
s0s1… sm
$X1…Xm aiai+1…an $
①如果ACTION [sm, ai]= sx,那么格局变为:
s0s1… sm x
$X1…Xmai ai+1…an $
②如果ACTION[sm , ai]= rx 表示用第x个产生式A→Xm-(k-1)…Xm进行归约,那么格局变为:
s0 s1… sm-k
$ X1…Xm-k A ai ai+1…an $
如果GOTO[sm-k , A]=y,那么格局变为:
s0 s1… sm-k y
$ X1…Xm-k A ai ai+1…an $
③如果ACTION[sm , ai]=acc,那么分析成功
④如果ACTION[sm , ai]=err ,那么出现句法错误
LR 分析算法
输入:串w和LR句法分析表,该表描述了文法G的ACTION函数和GOTO函数。
输出:如果w在 L(G)中,则输出w的自底向上句法分析过程中的归约步骤;否则给出错误指示。
方法:初始时,句法分析器栈中的内容为初始状态s0,输入缓冲区中的内容为w$。然后,句法分析器执行下面的程序:
令a为w$的第一个符号;
while(1) { /* 永远重复*/
令s是栈顶的状态;
if ( ACTION [s,a] = st ) {
将t压入栈中;
令a为下一个输入符号;
} else if (ACTION [s,a] =归约A → β ) {
从栈中弹出│ β │个符号;
将GOTO [t,A]压入栈中;
输出产生式 A → β ;
} else if (ACTION [s,a] =接受) break; /* 句法分析完成*/
else调用错误恢复例程;
}
LR(0)分析法
LR(0) 项目
右部某位置标有圆点的产生式称为相应文法的一个LR(0)项目(简称为项目)A→ α1·α2
项目描述了句柄识别的状态
产生式A→ε 只生成一个项目A→ ·
例子:S→bBB
移进项目:S → ·bBB
待约项目:S → b·BB;S → bB·B
归约项目:S → bBB·
增广文法 (Augmented Grammar)
如果G 是一个以S为开始符号的文法,则G的增广文法 G' 就是在G中加上新开始符号S' 和产生式S' → S而得到的文法
例子:
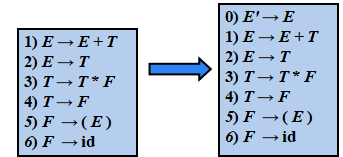
引入这个新的开始产生式的目的是使得文法开始符号仅出现在一个产生式的左边,从而使得分析器只有一个接受状态
文法中的项目
① S'→S ② S→vI:T ③ I→I,i ④ I→i ⑤ T →r
后继项目(Successive Item)
- 同属于一个产生式的项目,但圆点的位置只相差一个符号, 则称后者是前者的后继项目
- A→α· Xβ的后继项目是A→αX·β
可以把等价的项目组成一个项目集( I ) ,称为项目集闭包(Closure of Item Sets),每个项目集闭包对应着自动机的一个状态。
LR(0)自动机
例子:
文法:(0) S' → S (1) S → BB (2) B → aB (3) B → b
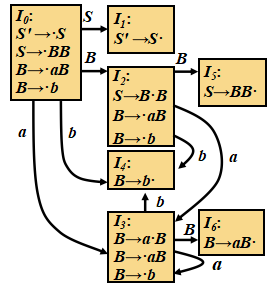
LR(0)分析表
状态 | ACTION | GOTO | |||
a | b | $ | S | B | |
0 | s3 | s4 | 1 | 2 | |
1 | acc | ||||
2 | s3 | s4 | 5 | ||
3 | s3 | s4 | 6 | ||
4 | r3 | r3 | r3 | ||
5 | r1 | r1 | r1 | ||
6 | r2 | r2 | r2 | ||
CLOSURE( )函数
计算给定项目集I的闭包
CLOSURE(I) = I∪{B→ · γ | A→α·Bβ∈CLOSURE(I), B→γ∈P}
SetOfltems CLOSURE ( I ) {
J = I;
repeat
for ( J中的每个项A → α∙Bβ )
for ( G的每个产生式B → γ )
if ( 项B → ∙ γ不在J中 )
将B → ∙ γ加入J中;
until 在某一轮中没有新的项被加入到J中;
return J;
}
返回项目集I对应于文法符号X的后继项目集闭包
GOTO( I, X )=CLOSURE({A→αX·β | A→α·Xβ∈I })
SetOfltems GOTO ( I,X ) {
将J 初始化为空集;
for ( I 中的每个项A → α∙Xβ )
将项 A → αX∙β 加入到集合J 中;
return CLOSURE ( J );
}
构造LR(0)自动机的状态集
规范LR(0) 项集族(Canonical LR(0) Collection)
C={I0}∪{I | 存在J∈C, X∈VN∪VT , I=GOTO(J , X) }
void items( G' ) {
C={ CLOSURE ({[ S'→ ·S ] } ) };
repeat
for (C中的每个项集 I )
for(每个文法符号X )
if ( GOTO ( I,X )非空且不在C中)
将GOTO ( I,X )加入C中;
until在某一轮中没有新的项集被加入到C中;
}
LR(0)分析表构造算法
构造G'的规范LR(0)项集族C = { I0, I1, … , In}
令Ii对应状态i。状态i的句法分析动作按照下面的方法决定:
- if A→α·aβ∈Ii and GOTO( Ii , a )=Ij then ACTION[ i, a ]=sj
- if A→α.Bβ∈Ii and GOTO( Ii , B )=Ij then GOTO[ i, B ]=j
- if A→α·∈Ii 且A ≠ S' then for 任意a∈VT∪{$} do ACTION[ i, a ]=rj (j是产生式A→α的编号)
- if S'→S· ∈Ii then ACTION [ i, $ ]=acc
没有定义的所有条目都设置为“error”
LR(0) 自动机的形式化定义
文法:G = ( VN , VT , P , S )
LR(0)自动机:M = ( C, VN∪VT , GOTO, I0 , F )
- C={I0}∪{I | 存在J∈C, X∈VN∪VT, I=GOTO(J,X ) }
- I0=CLOSURE({S′ →.S })
- F={ CLOSURE({S′ →S.}) }
LR(0) 分析过程中的冲突
例子:移进/归约冲突
文法: (0) E′ → E (1) E → E+T (2) E → T (3) T → T*F (4) T → F (5) F → (E) (6) F → id
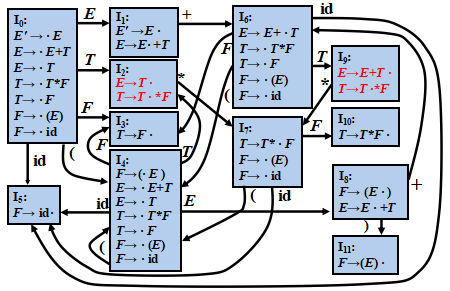
表达式文法的LR(0)分析表含有移进/归约冲突
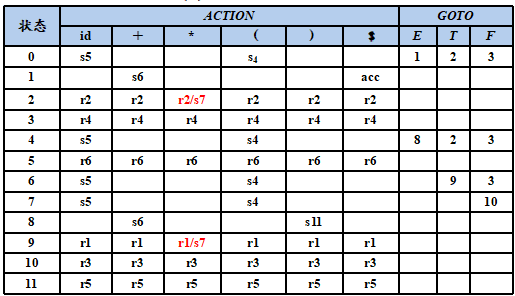
如果LR(0)分析表中没有句法分析动作冲突,那么给定的文法就称为LR(0)文法
不是所有CFG都能用LR(0)方法进行分析,也就是说,CFG不总是LR(0)文法
归约/归约冲突
文法:(0) S′→ T (1) T → aBd (2) T → ε (3) B →Tb (4) B → ε
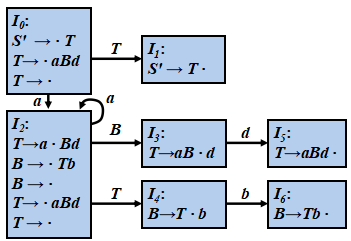
SLR分析
SLR分析法的基本思想
已知项目集 I:
m个移进项目:
A1→α1.a1β1
A2→α2.a2β2
…
Am→αm.amβm
n个规约项目:
B1→γ1.
B2→γ2.
…
Bn→γn.
如果集合{a1, a2, …, am}和FOLLOW(B1), FOLLOW(B2),…,FOLLOW(Bn)两两不相交,则项目 集I中的冲突可以按以下原则解决:
设a是下一个输入符号
- 若a∈{ a1, a2, …, am },则移进a
- 若a∈FOLLOW(Bi),则用产生式 Bi→γi 归约
- 此外,报错
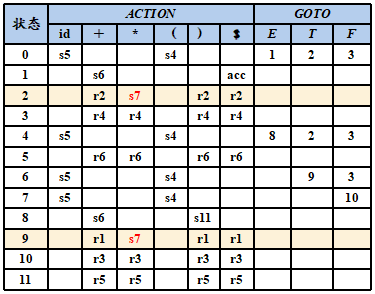
例子:
文法 (0) S′→ T (1) T → aBd (2) T → ε (3) B →Tb (4) B → ε
FOLLOW(S′ )={ $ } FOLLOW(T)={ $, b } FOLLOW(B)={ d }
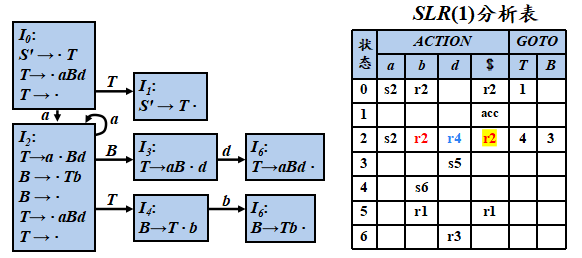
SLR 分析表构造算法
构造G'的规范LR(0)项集族C = { I0, I1, … , In}。
根据Ii构造得到状态i。状态i 的句法分析动作按照下面的方法决定:
- if A→α·aβ∈Ii and GOTO( Ii , a )=Ij then ACTION[ i, a ]=sj
- if A→α.Bβ∈Ii and GOTO( Ii , B )=Ij then GOTO[ i, B ]=j
- if A→α·∈Ii且A ≠ S' then for 任意a∈FOLLOW(A) do ACTION[ i, a ]=rj (j是产生式A→α的编号)
- if S'→S·∈Ii then ACTION [ i , $ ]=acc;
没有定义的所有条目都设置为“error”。
如果给定文法的SLR分析表中不存在有冲突的动作,那么该文法称为SLR文法。
SLR 分析中的冲突
例子:0) S′→S 1) S→L=R 2) S→R 3) L→*R 4) L→id 5) R→L
FOLLOW(R) = { =,$ }
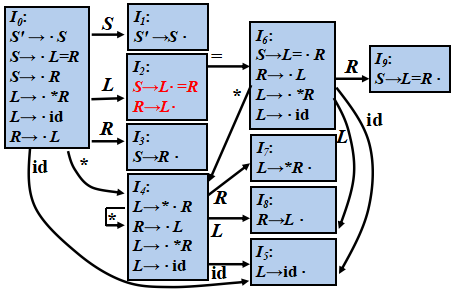
在I2,遇到等号可以选择移进,但是FOLLOW(R)包含=,所以也可以选择5规约,所以冲突。
LR(1)分析
LR(1)分析法的提出
SLR分析存在的问题
SLR只是简单地考察下一个输入符号b是否属于与归约项目A→α相关联的FOLLOW(A),但b∈FOLLOW(A)只是归约α的一个必要条件,而非充分条件
- 不含句柄右侧任一符号的规范句型前缀称为该句型的活前缀(viable prefix)。
- 假设符号栈中符号串为δαβ,输入指针指向终结符a ;如果想实施规约动作A→αβ ,那么δAa应为规范句型(right-sentential form)的前缀。
- 构造[A→α·β, a],通过选择a使得δAa为某一规范句型前缀, LR(1) 项。
- [A→α·β, a] is valid if
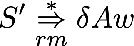 ,a = The first character of w ($ if w=ε).
,a = The first character of w ($ if w=ε). - [S’→·S, $] is valid since S’$ is a right-sentential form.
规范LR(1)项目
- 将一般形式为 [A→α·β, a]的项称为 LR(1) 项,其中A→αβ 是一个产生式,a 是一个终结符(这里将$视为一个特殊的终结符)它表示在当前状态下,A后面必须紧跟的终结符,称为该项的展望符(lookahead) 。
- LR(1) 中的1指的是项的第二个分量的长度
- 在形如[A→α·β, a]且β ≠ ε的项中,展望符a没有任何作用
- 但是一个形如[A→α·, a]的项在只有在下一个输入符号等于a时才可以按照A→α 进行归约 。这样的a的集合总是FOLLOW(A)的子集,而且它通常是一个真子集
一、什么是 LR(1) 项?
LR(1) 项的标准形式是这样的:[A → α·β, a]
它包含 三个部分:
产生式:A → αβ(原本的文法规则)
点(·)的位置:表示“分析器读到了哪里”,·之前的部分已经处理完,·后面的部分还没处理。
展望符(lookahead)a:表示“当下一个输入符号是 a 的时候”,这个项目才有效(只在特定的情形下才允许归约)。
二、LR(1) 中的“1”是什么意思?
这个 “1” 指的是:展望符 lookahead 的长度是 1 个终结符,也就是说,我们只“看”下一个输入符号,不是两个或多个。
三、举例说明
比如你有一个产生式:A → α
那么可能出现的 LR(1) 项是:[A → α·, a]
这表示:
这个产生式已经读完了(点在最右边),
但是我们只有在接下来的输入是
a时,才能对 A 进行归约。四、什么时候展望符有用,什么时候没用?
情况 1:点不在最后(还有 β 要读)
比如:[A → α·β, a]
这时我们还没读完
β,还要继续移进(shift),所以展望符 a 没什么用处,只是记录在案。情况 2:点在最后(可以归约了)
比如:[A → α·, a]
这时
α已经读完,我们要归约A → α,但!只有当下一个输入符号是 a 的时候,才能进行归约!这就是展望符真正起作用的地方!五、为什么说展望符是 FOLLOW(A) 的子集?
因为在文法分析中,我们只有当“接下来能接在 A 后面的符号”出现在输入中时,才可以归约 A。这些“能接在 A 后面的符号”就叫做
FOLLOW(A)。但在 LR(1) 项中,我们不一定收集 FOLLOW(A) 的所有符号,只需要记录当前这条路径中可能出现的那个终结符就够了。所以:
展望符
a属于 FOLLOW(A)但一般来说只是其中的一个子集(甚至是一个符号)
总结:LR(1) 项 [A→α·, a] 的意思是:我们已经识别出 α,只有当接下来的输入符号是 a 的时候,才能归约为 A。
等价LR(1)项目
[ A→α·Bβ, a ] ------(B→γ∈P)-------[ B→·γ, b ]b∈FIRST (βa)
当β ⇒+ ε时,此时b=a叫继承的后继符, 否则叫自生的后继符
[ A → α·Bβ, a ]
↓
(B → γ ∈ P)
↓
[ B → ·γ, b ],其中 b ∈ FIRST(βa)
这实际上描述的是如何从一个 LR(1) 项生成一个新的 LR(1) 项,我们称它为等价 LR(1) 项的推导关系(closure)。(1)原始项:[ A → α·Bβ, a ]
表示我们正在处理产生式 A → αBβ,其中已经处理完 α,接下来要处理 Bβ,当前展望符为 a。
(2)产生式展开
因为当前要处理
B,所以我们要把文法中所有形如:B → γ,的产生式都列出来。(3)项扩展(闭包)
于是我们生成新的 LR(1) 项:[ B → ·γ, b ]
b 的集合是 FIRST(βa)
--》为什么是 FIRST(βa)?
我们当前正在处理
A → α·Bβ,并希望展开B → γ。
接下来我们会读
β,最终希望看到a。所以我们需要分析:在处理完 B → γ 之后,会出现什么终结符?
答案是:
β后接a,这整体构成了上下文。因此我们需要:b ∈ FIRST(βa)
--》什么是继承的后继符?
如果
β ⇒+ ε(即 β 能推出空串),那么:FIRST(βa) 就包含 a因为 β 消失了,就要“看到”a。所以这个展望符 a 就被继承到了新项中:b = a → 继承的后继符
--》什么是自生的后继符?
如果 β 无法推出 ε(不能为空),那么:FIRST(βa) = FIRST(β)
也就是说,后继符
b是由 β 自己推导出来的,不是从 a 继承来的。这时候的
b就叫:b ≠ a → 自生的后继符
例子:
文法如下:S → A a;A → b | ε
分析项:[S → ·A a, $]
当前点在 A 前面,要展开 A
β = a,a 是终结符,不能推出 ε
所以:FIRST(βa) = FIRST(a$) = {a}
得到等价项:
[A → ·b, a] 自生的后继符
[A → ·ε, a] 自生的后继符(ε 表示空)
再看一个例子:
S → A B;A → ε;B → b
分析项:[S → A·B, $]
点在 B 前面,要展开 B,β = 空,a = $
此时:FIRST(βa) = FIRST($) = {$}
β 可以推出 ε,所以 $ 这个展望符是继承来的 → 称为“继承的后继符”。
LR(1)自动机
例子
文法:0) S′ →S 1) S→L=R 2) S→R 3) L→*R 4) L→id 5) R→L
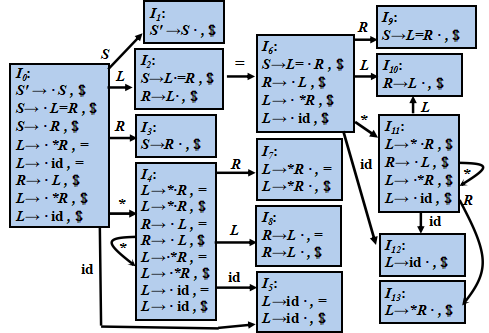
赋值语句文法的 LR(1)分析表
状态 | ACTION | GOTO | |||||
* | id | = | $ | S | L | R | |
0 | s4 | s5 | 1 | 2 | 3 | ||
1 | acc | ||||||
2 | s6 | r5 | |||||
3 | r2 | ||||||
4 | s4 | s5 | 8 | 7 | |||
5 | r4 | r4 | |||||
6 | s11 | s12 | 10 | 9 | |||
7 | r3 | r3 | |||||
8 | r5 | r5 | |||||
9 | r1 | ||||||
10 | r5 | ||||||
11 | s11 | s12 | 10 | 13 | |||
12 | r4 | ||||||
13 | r3 | ||||||
如果除展望符外,两个LR(1)项目集是相同的,则称这两个LR(1)项目集是同心的
LR(1)项目集闭包
CLOSURE( I ) = I ∪{ [B→·γ, b] | [A→α·Bβ, a] ∈ CLOSURE( I ), B→γ∈P, b∈FIRST(βa)}
SetOfltems CLOSURE ( I ) {
repeat
for ( I中的每个项[A → α∙Bβ,a ])
for (G'的每个产生式B → γ)
for ( FIRST (βa)中的每个符号b )
将[ B → ∙ γ ,b]加入到集合I中;
until 不能向I中加入更多的项;
until I ;
}
当我们在某个状态中遇到了一个形如:[A → α·Bβ, a]
因为我们即将识别 B,所以需要把 B 的所有产生式都加进来,比如:B → γ
对这些新加入的项目:[B → ·γ, b],b 来自于 FIRST(βa)也就是 B 后面那一串 βa 的首符号集合
GOTO 函数
GOTO( I, X ) = CLOSURE({[A→αX·β,a]|[A→α·Xβ, a]∈I })
SetOfltems GOTO ( I,X ) {
将J 初始化为空集;
for ( I 中的每个项[A → α∙Xβ,a ])
将项[ A → αX∙β,a]加入到集合J 中;
return CLOSURE ( J );
}
GOTO 就是状态转移:如果在状态 I 中看到了符号 X(可以是终结符也可以是非终结符),那你将转移到哪个状态?
[A → α·Xβ, a] 变成:[A → αX·β, a]
然后再对它们求 CLOSURE,得到的新集合就是 GOTO(I, X)。
为文法G' 构造LR(1)项集族
void items (G' ) {
将C初始化为{CLOSURE ({[ S' → ∙ S, $]} )} ;
repeat
for ( C中的每个项集 I )
for ( 每个文法符号X )
if (GOTO(I,X )非空且不在C中)
将GOTO(I,X )加入C中;
until 不再有新的项集加入到C中;
}
构造完整 LR(1) 自动机的步骤(items(G'))
(1)初始化起始项:I0 = CLOSURE({[S' → ·S, $]})
(2)初始化项目集族:C = {I0}
(3)不断对 C 中每个项集 I,尝试所有符号 X:
如果:GOTO(I, X) = 新集合 I' 且 I' 不在 C 中
就加入到 C 中。一直到没有新项集加入为止。
这就构成了 LR(1) 项目集规范族,也就是 自动机的状态集合 C。
LR(1)自动机的形式化定义
文法: G = (VN , VT , P, S )
LR(1)自动机 : M = (C, VN∪VT , GOTO, I0 , F )
- C={I0}∪{I | 存在J∈C, X∈VN∪VT, I=GOTO(J,X ) }
- I0=CLOSURE({S' →·S, $})
- F={ CLOSURE({S'→S· , $}) }
LR分析表构造算法
构造G'的规范LR(1)项集族C = { I0, I1, … , In}
根据Ii构造得到状态i。状态i 的句法分析动作按照下面的方法决定:
- if [A→α·aβ, b ] ∈Ii and GOTO( Ii , a )=Ij then ACTION[ i, a ]=sj
- if [A→α·Bβ,b ] ∈Ii and GOTO( Ii , B )=Ij then GOTO[ i, B ]=j
- if [A→α·, a ] ∈Ii且A ≠ S' then ACTION[ i, a ]=rj (j是产生式A→α的编号)
- if [S'→S·, $] ∈Ii then ACTION [ i, $ ]=acc;
没有定义的所有条目都设置为“error”
构造 LR(1) 分析表(ACTION 和 GOTO)
ACTION 表的构造(终结符对应的移进、归约、接受动作):
| 条件 | 动作 |
|---|---|
[A → α·aβ, b] 且 GOTO(Ii, a) = Ij | ACTION[i, a] = sj(移进) |
[A → α·, a] 且 A ≠ S' | ACTION[i, a] = rj(归约) |
[S' → S·, $] | ACTION[i, $] = acc(接受) |
如果LR(1)分析表中没有句法分析动作冲突,那么给定的文法就称为LR(1)文法
LALR分析法
LALR ( lookahead-LR )分析的基本思想
- 寻找具有相同核心的LR (1) 项集,并将这些项集合并为一个项集。 所谓项集的核心就是其第一分量的集合
- 然后根据合并后得到的项集族构造句法分析表
- 如果分析表中没有句法分析动作冲突,给定的文法就称为LALR (1) 文法,就可以根据该分析表进行句法分析
合并同心项集
例子
LALR自动机
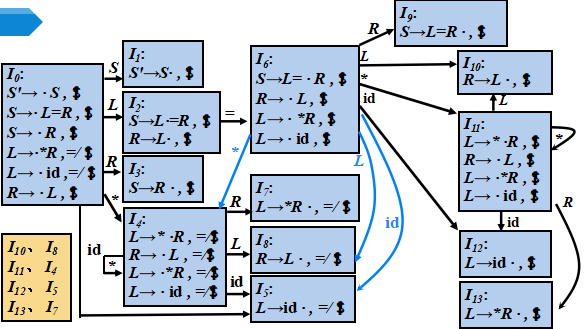
合并后:
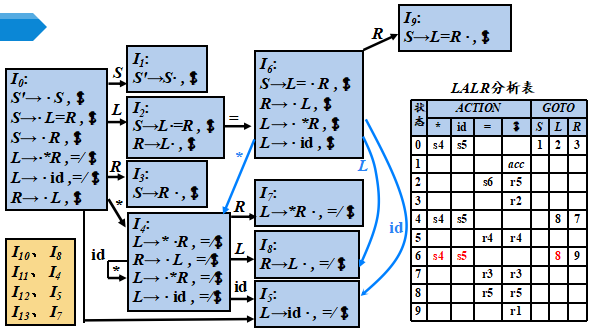
合并同心项集时产生归约-归约冲突的例子
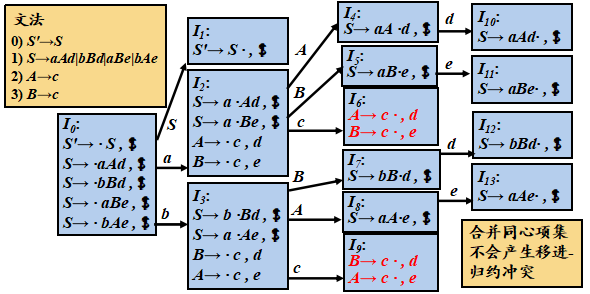
合并同心项集后,虽然不产生冲突,但可能会推迟错误的发现
LALR分析法可能会作多余的归约动作, 但绝不会作错误的移进操作
LALR(1)的特点
- 形式上与LR(1)相同
意思是:
LALR(1) 的 分析表(ACTION 和 GOTO 格式) 和 LR(1) 完全一样。你用它分析语句的方式、状态编号、项的写法什么的,看起来都像 LR(1)。
- 大小上与LR(0)/SLR相当
LR(1) 的表格特别大,因为它的每个状态都带一个展望符(lookahead)。
而 LALR(1) 通过合并一些“看起来很像”的状态,大大压缩了表格大小。
所以它的大小差不多等于 SLR 或者 LR(0),这就更节省空间。
- 分析能力介于SLR和LR(1)二者之间:SLR<LALR(1)<LR(1)
| 方法 | 分析能力 | 表格大小 |
|---|---|---|
| SLR | 最弱 | 最小 |
| LALR(1) | 中等(比SLR强) | 中等 |
| LR(1) | 最强 | 最大 |
举个例子:某些复杂文法,SLR 会冲突(无法决定移进还是归约),但 LALR(1) 可以正确处理。再更复杂一点的,可能只有 LR(1) 能处理。
- 合并后的展望符集合仍为FOLLOW集的子集。
先解释什么是“合并”:LALR(1) 是通过把具有相同 LR(0) 样子的状态合并,来得到更小的状态集合。
但是它不会随便乱合并:它会把展望符集合(lookahead set)也合并在一起。合并后新状态的展望符,还是 FOLLOW 集的子集(不会乱加非法符号)
这就保证了语法分析不会出现错误。
可以把三种方法想成三个保安在查票:
| 方法 | 比喻 |
|---|---|
| SLR | 只看票上有没有名字,管得松,容易出错,但速度快。 |
| LR(1) | 不光看票,还问你下一站去哪儿,查得特别严,一点也不含糊,但太慢,太啰嗦。 |
| LALR(1) | 看票也问你去哪儿,但多个保安合并值班,效率高,处理大多数情况也不出错。 |
LALR(1) 是一种折中方法,它保留了大部分 LR(1) 的分析能力,但用了更小的状态集来减少分析表的大小,因此实用性很高。
二义性文法的LR分析
二义性文法的特点
每个二义性文法都不是LR的
某些类型的二义性文法在语言的描述和实现中很有用(更简短、更自然)
一个文法是二义性的(ambiguous),如果:存在一个句子,它有两棵不同的语法分析树(或者两个不同的右推导或左推导)。也就是说,一个句子可能被文法“解释成两种不同意思”。
一个文法是 LR 文法,比如 LR(0)、SLR(1)、LALR(1)、LR(1),意思是:它可以被构造出没有冲突的 LR 分析表,通过 自底向上(shift-reduce) 的方式,用一个有限状态自动机准确分析。
关键点:LR 文法必须是“确定的”、“无二义性的”。
为什么“每个二义性文法都不是 LR 的”?
LR 分析器只能为每个输入构建一棵唯一的分析树。
它的语法分析表必须是无冲突的,这意味着:每一个状态 + 输入符号,都只能有一个明确的动作(要么移进、要么归约、要么接受)。如果一个句子有多种解释(即有多棵分析树) ⇒ 就必定导致冲突
所以,如果一个文法本身是二义性的,那无论你怎么构造 LR 表,总会产生冲突(移进-归约冲突或归约-归约冲突)。这就意味着:这个文法不可能是 LR 的。
不是 LR 的文法 不一定是二义性的(它也可能只是太复杂,无法构建 LR 表)
但是:二义性文法一定不是 LR 的。
二义性算术表达式文法的SLR分析器
例:
文法:E→E+E; E→E*E ;E→(E) ;E→id
用优先级和结合性解决冲突(FOLLOW(E) = { +,*,), $ })
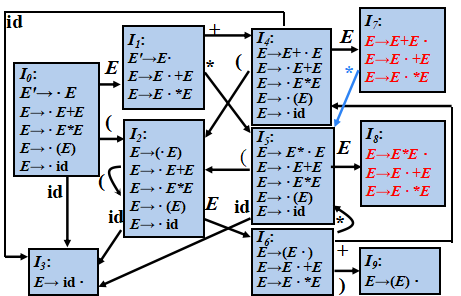
状态 | ACTION | GOTO | |||||
id | + | * | ( | ) | $ | E | |
0 | s3 | s2 | 1 | ||||
1 | s4 | s5 | acc | ||||
2 | s3 | s2 | 6 | ||||
3 | r4 | r4 | r4 | r4 | |||
4 | s3 | s2 | 7 | ||||
5 | s3 | s2 | 8 | ||||
6 | s4 | s5 | s9 | ||||
7 | r1 | s5 | r1 | r1 | |||
8 | r2 | r2 | r2 | r2 | |||
9 | r3 | r3 | r3 | r3 | |||
例:二义性if 语句文法的LR分析

S → i S| i S e S | a
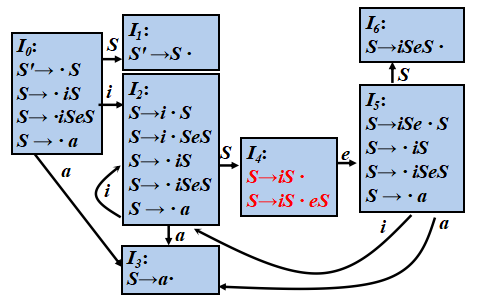
二义性if语句文法的SLR分析表
状态 | ACTION | GOTO | |||
i | e | a | $ | S | |
0 | s2 | s3 | 1 | ||
1 | acc | ||||
2 | s2 | s3 | 4 | ||
3 | r3 | r3 | |||
4 | s5 | r1 | |||
5 | s2 | s3 | 6 | ||
6 | r2 | r2 | |||
二义性文法的使用
应该保守地使用二义性文法,并且必须在严格控制之下使用,因为稍有不慎就会导致句法分析器所识别的语言出现偏差
练习题
练习题1
(1)S→v I : T (2) I→i (3) I→I , i (4) T→real (5) T→ int
1)画出其LR(0)自动机((0) S’ → S)
2)构造LR(0)分析表
3)给出LR(0)自动机在分析输入v i, i : real时分析栈和剩余输入的变化过程
练习题2
(1)S→A (2) A→BA | ε (3) B→aB | b
1)试用识别活前缀的方式给出文法 G 的 LR(1)项目集。
2)构造 G 的 LR(1)分析表。
3)给出输入符号串abab的自底向上语法分析过程。
LR分析中的错误处理
句法错误的检测:当LR分析器在查询分析表并发现一个报错条目时,就检测到了一个句法错误
错误恢复策略:恐慌模式错误恢复;短语层次错误恢复
恐慌模式错误恢复
s0s1… si si+1 … sm
$X1…Xi A … Xm
- 从栈顶向下扫描,直到发现某个状态si,它有一个对应于某个非终结符A的GOTO目标,可以认为从这个A推导出的串中包含错误
- 然后丢弃0个或多个输入符号,直到发现一个可能合法地跟在A之后的符号a为止。
- 之后将si+1 = GOTO(si , A)压入栈中,继续进行正常的句法分析
短语层次错误恢复
- 检查LR分析表中的每一个报错条目,并根据语言的使用方法来决定程序员所犯的何种错误最有可能引起这个句法错误
- 然后构造出适当的恢复过程
例:算数表达式文法的LR分析器
文法:E→E+E; E→E*E; E→(E) ;E→id
VT ={+,*,(,),id, $}
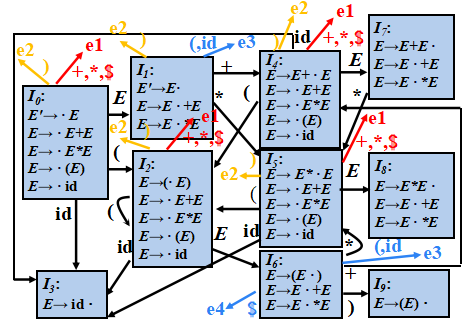
带有错误处理子程序的算术表达式文法LR分析表
错误处理例程
- e1:将状态3压入栈中,发出诊断信息“缺少运算分量”
- e2:从输入中删除“)”,发出诊断信息“不匹配的右括号”
- e3:将状态4压入栈中,发出诊断信息“缺少运算符”
- e4:将状态9压入栈中,发出诊断信息“缺少右括号”
状态 | ACTION | GOTO | |||||
id | + | * | ( | ) | $ | E | |
0 | s3 | e1 | e1 | s2 | e2 | e1 | 1 |
1 | e3 | s4 | s5 | e3 | e2 | acc | |
2 | s3 | e1 | e1 | s2 | e2 | e1 | 6 |
3 | r4 | r4 | r4 | r4 | r4 | r4 | |
4 | s3 | e1 | e1 | s2 | e2 | e1 | 7 |
5 | s3 | e1 | e1 | s2 | e2 | e1 | 8 |
6 | e3 | s4 | s5 | e3 | s9 | e4 | |
7 | r1 | r1 | s5 | r1 | r1 | r1 | |
8 | r2 | r2 | r2 | r2 | r2 | r2 | |
9 | r3 | r3 | r3 | r3 | r3 | r3 | |
LR(1)分析法的提出
不含句柄右侧任一符号的规范句型前缀称为该句型的活前缀(viable prefix)。
假设符号栈中符号串为δα,输入指针指向终结符a ;如果想实施规约动作A→α,那么δAa应为某一规范句型(right-sentential form)的前缀。
构造[A→α·β, a],通过选择a使得δAa为某一规范句型前缀。
[A→α·β, a] is valid if ![]() ,a = The first character of w ($ if w=ε).
,a = The first character of w ($ if w=ε).
[S’→·S, $] is valid, this is our initial item, ![]() ,A=S^′, β=S, δ=α=w=ε.
,A=S^′, β=S, δ=α=w=ε.
