信奥之计算原理与排列组合

加乘原理

1.加法原理（求和法则）

如果完成一件事情，有n类方法:第1类有a种方法，第2类有b种方法，第3类有c种方法…只能选择其中的一类，不能同时选择，则一共的方法数量:
                                                                a+b+c+…n

例:一所大学正在从数学系的成员中选拔一位代表加入校学术委员会。候选人可以是数学系的教师或者数学系的学生。目前，数学系有教师30人，学生80人。问:有多少种不同的方式来选择这位校学术委员会的代表?

                                                30+80=110

2.乘法原理（乘积法则）

你准备出门去参加一个派对，你有2件不同的T恤(一件红色，一件蓝色)和3条不同的裤子(一条黑色，一条灰色，一条蓝色)。那么，你有多少种不同的穿衣组合可以选择呢?

如果完成一件事情，有n个步骤:第1个步骤有a种方法，第2个步骤有b种方法，第3个步骤有c种方法…各个步骤按顺序来，每个步骤选择一种方法，总共的方法数量:

                                                                axbxc...n

假设你是一家餐厅的菜单设计师，你需要为午餐设计一个套餐，套餐包括一个主菜和一份饮料。餐厅提供以下选项:

主菜:  有意大利面、披萨和汉堡三种选择。

饮料:  汽水、果汁两种选择。

1、如果一个套餐包括一种主菜和一种饮料，那么总共有多少种不同的套餐组合?

2、如果餐厅决定在披萨中加入两种新口味: 辣味披萨和蘑菇披萨，同时在果汁中也增加了两种选择:苹果汁和橙汁，那么现在总共有多少种不同的套餐组合?

第一问: 3 * 2 = 6

第二问:  5 * 4 = 20

排列组合

排列

从几个不同元素中取出r(r≤n)个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出r个元素的一个排列，方案数为 A

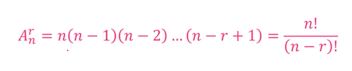
n! = n * (n - 1) *......*2*1

4! = 4 * 3 * 2 * 1 = 12

A也可记作A（n，r）、P（n,r）、P

例题:

4个风景点(abcd)中选出2个，并确定这2个风景点的先后游览顺序，有多少种不同的方法?

 

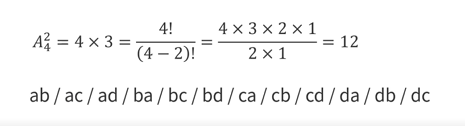
例题:

分别从6个不同的乒乓球中选择3个乒乓球，依次放在3个不同的盒子里，每个盒子1个，请问有多少种放法?

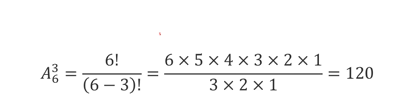
练习:

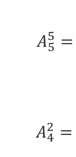分别等于多少？

组合

从n个不同元素中取出r(r≤n)个元素的所有组合的个数，叫做从n个不同元素中取出r个元素的组合数，方案数为C表示。

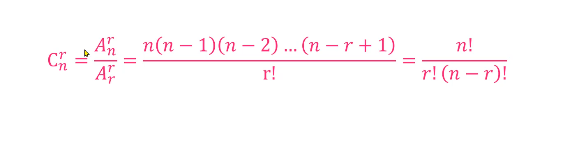
组合与排列的区别在于是否有顺序

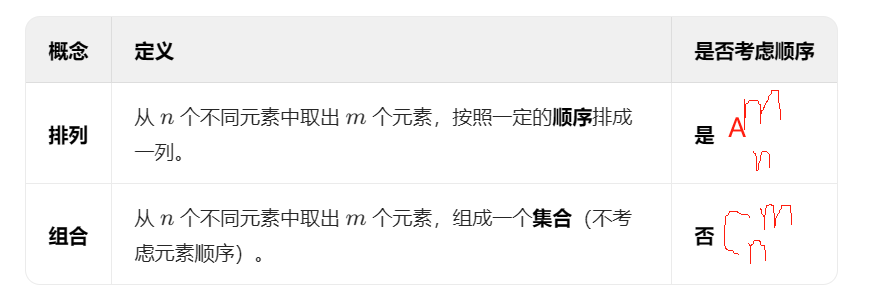
练习:

在某高校文化节上，四个学院--文学院(甲)、理学院(乙)、工学院(丙)和艺术学院(丁)--决定举行一场辩论赛。比赛采取单循环制，即每个学院都要与其他各学院各辩论一次。
问题一:这四个学院总共需要举办多少场辩论赛?请列出所有辩论赛的对阵情况。
问题二:在这场辩论赛中，有多少种可能的冠亚军组合?请列出所有冠亚军的可能组合。

问题一: 四个学院 两两辩论，组合 C=6。

问题二:  A  有排序，所以是排列。

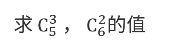
组合公式

C = C  理解:从几个人中选出r个人，和从几个人中淘汰-r个人，是一样的

C = C + C  比如 求，如果要完成从5个人选出3个人，有两种途径

第一种:选第5个人，然后前4个人中选2个，也就是C

第二种:不选第5个人，然后前4个人中选3个，也就是C

所以根据加法原理， C=C+ C。

计数导论

1.特殊优先

特殊元素，优先处理;特殊位置，优先考虑
例如题目中出现以下字样，我们考虑特殊优先!：

甲在排头

甲乙不相邻

丙必须在丁前面。。。。

例题:

6个人站成一排，求:甲、乙既不在排头也不在排尾的排法数?

方法一:

方法二:

 

 特殊优先

6个人站成一排，求:甲不在排头，乙不在排尾，且甲乙不相邻的排法数

捆绑法

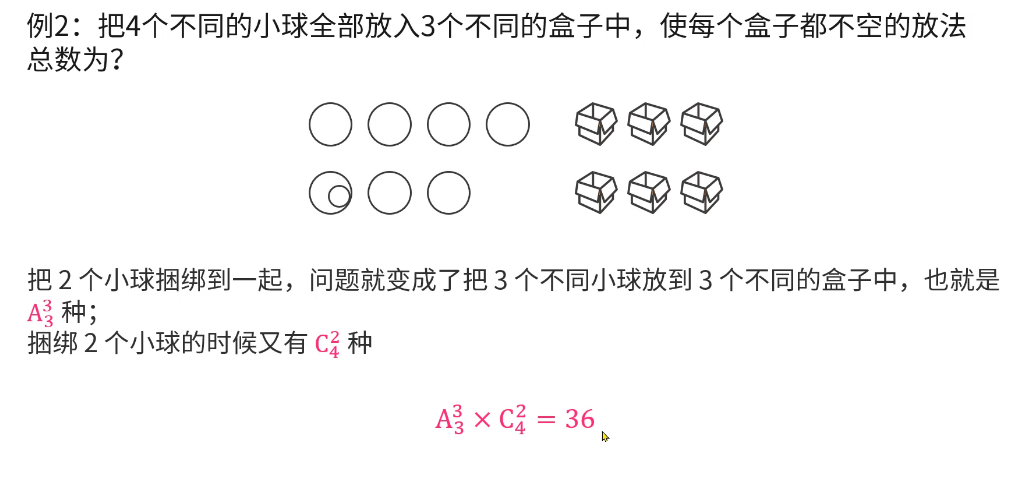
 插板法

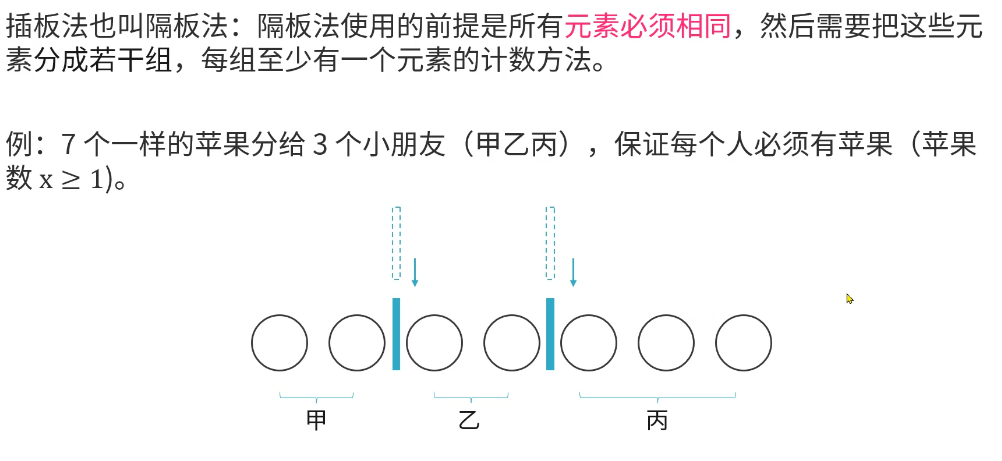
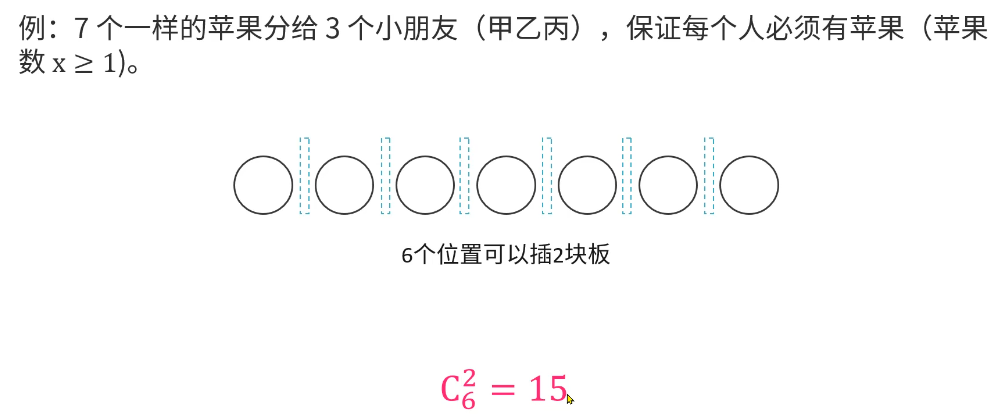
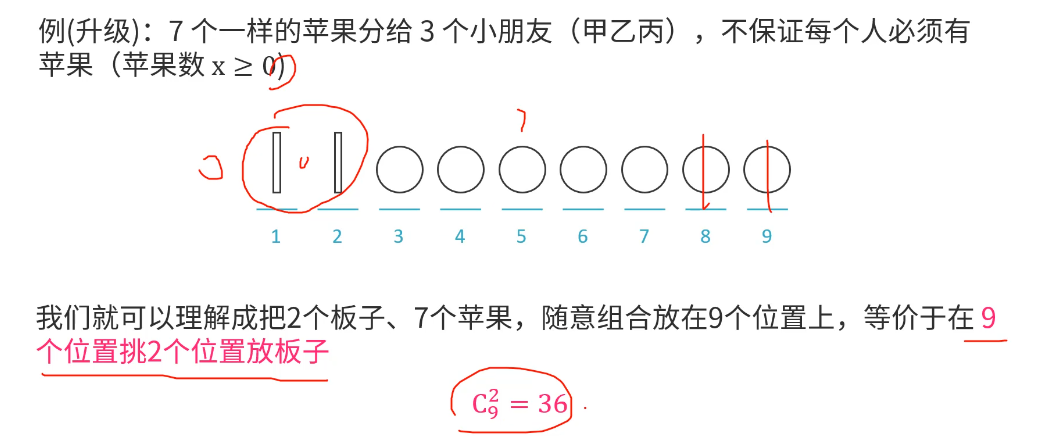
插板法总结

可重复排列

小球盒子的问题

 

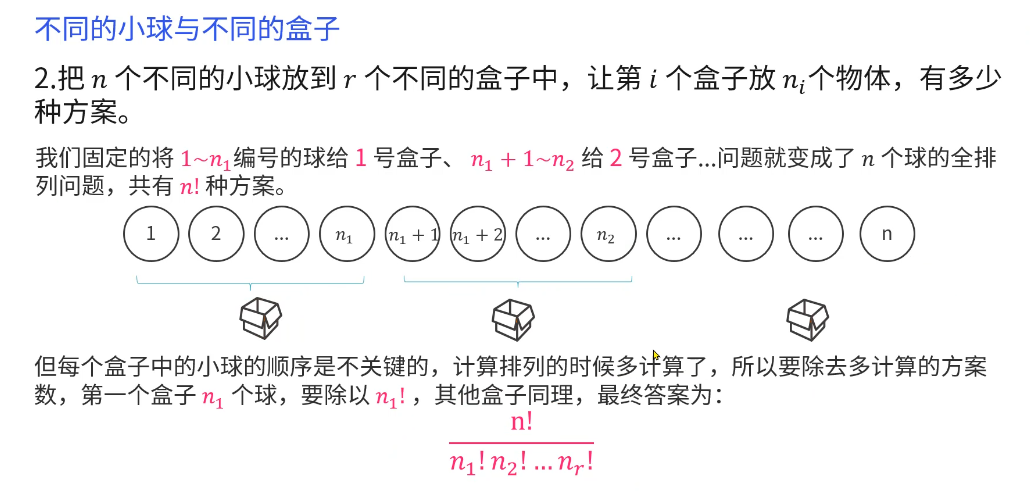
万能法