力扣hot100:矩阵置零（73）（原地算法）

今天本来准备好好补一下智能客服项目的，但因为纳新网站占了不分时间没弄成，简单做了两个算法，看了下八股

问题描述

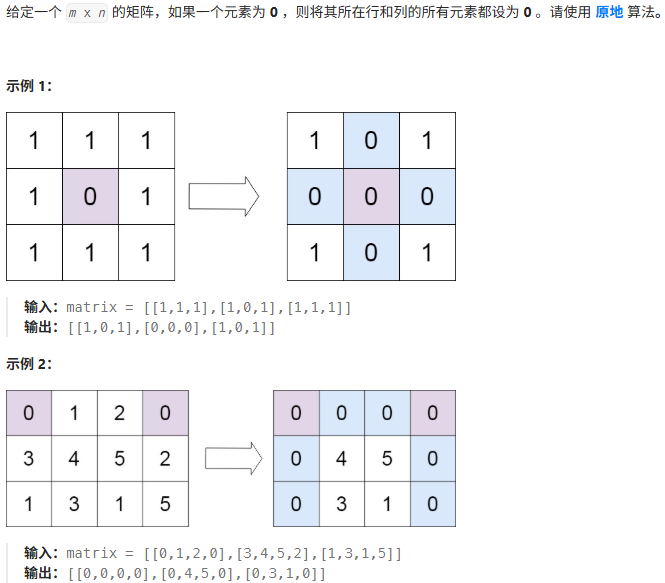
核心思路

1. 标记需清零的行列

   • 创建两个布尔数组 arr（长度=行数）和 brr（长度=列数），分别标记需要清零的行和列。
   • 遍历矩阵，遇到元素为 0 时，将对应行索引在 arr 中标记为 true，列索引在 brr 中标记为 true。

2. 执行清零操作

   • 再次遍历矩阵，若当前行或列被标记为需清零，则将元素置为 0。

时间复杂度：O(m × n) 空间复杂度：O(m + n)（两个额外数组）

代码实现

class Solution {public void setZeroes(int[][] matrix) {int x= matrix.length;int y=matrix[0].length;boolean[] arr = new boolean[x];boolean[] brr=new boolean[y];for(int i=0;i<x;i++){for(int j=0;j<y;j++){if(matrix[i][j]==0){arr[i]=brr[j]=true;}}}for(int i=0;i<x;i++){for(int j=0;j<y;j++){if(arr[i]||brr[j]){matrix[i][j]=0;}}}}
}

关键步骤解析

1. 初始化标记数组

   • rowZero 数组标记需清零的行（长度为 m），colZero 数组标记需清零的列（长度为 n）。
   • 默认值均为 false，表示初始时无需清零。

2. 第一次遍历：标记清零位置

   • 遍历每个元素 matrix[i][j]，若值为 0，则设置 rowZero[i] = true 和 colZero[j] = true。
   • 示例： 矩阵 [[1,0,1],[1,1,1],[1,1,0]] 的标记结果为： rowZero = [true, false, true]（第0行和第2行需清零） colZero = [true, false, true]（第0列和第2列需清零）

3. 第二次遍历：执行清零

   • 遍历每个元素，若 rowZero[i] 或 colZero[j] 为 true，则置零。
   • 逻辑解释：
     • 若当前行需清零（rowZero[i]==true），则无论列是否标记，该行所有元素清零。
     • 若当前列需清零（colZero[j]==true），则无论行是否标记，该列所有元素清零。

示例演示

输入矩阵：

[[1, 0, 1],[1, 1, 1],[1, 1, 0]
]

标记过程：

1. 遍历到 (0,1)=0 → 标记 rowZero=true, colZero=true。
2. 遍历到 (2,2)=0 → 标记 rowZero=true, colZero=true。

清零过程：

• 第0行：全部清零 → [0,0,0]
• 第2行：全部清零 → [0,0,0]
• 第1行：第1列被标记 → [1,0,1] → 但第1行未被标记，因此仅第1列清零 → [1,0,1] 变为 [1,0,1]（实际不变）

输出矩阵：

[[0, 0, 0],[1, 0, 1],  // 第1列被标记清零，其他元素保留[0, 0, 0]
]

优化思考

虽然此解法空间复杂度为 O(m+n)，但若追求 O(1) 空间，可将矩阵的第一行和第一列作为标记数组（需额外变量处理第一行/列的初始状态）。核心思想类似，但需注意边界条件，适合进阶挑战！

通过两个布尔数组的巧妙使用，我们高效地解决了矩阵置零问题。这种“标记-清零”的分步策略清晰易懂，是处理矩阵类问题的经典思路。