2025国赛B题保姆级教程思路分析 碳化硅外延层厚度的确定
2025国赛B题保姆级教程思路分析
B题:碳化硅外延层厚度的确定
第一问
在考虑一次反射和透射的情形下,外延层厚度的测量依赖于干涉条纹的形成。为了建立数学模型,我们可以通过以下几个步骤:
1. 干涉原理
当红外光照射到外延层时,会发生两次反射:
第一次反射:外延层与空气界面上的反射。
第二次反射:外延层与衬底界面上的反射。
这些反射光波会相互干涉,从而形成干涉条纹。
2. 干涉条件
假设干涉条纹是由两束反射光产生的。它们的相位差会影响干涉条纹的形成。
反射光的相位差:
光波在两次反射过程中会经历不同的路径差。由于外延层和衬底的折射率不同,因此两束反射光在传播过程中会经历不同的折射,从而产生相位差。为了计算相位差,需要考虑以下因素:
波数(v)与波长的关系:波数和波长成反比。
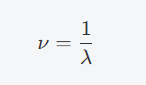
折射率(n):外延层和衬底的折射率会影响光的传播速度,从而影响光的路径差。
路径差:
设外延层的厚度为 d,入射角为 θ,红外光波的波长为 λ,外延层的折射率为 n。从反射的角度来看,光波在外延层内传播的实际路径为:

因此,光波的总路径差为 2l(反射路径的两倍),我们可以得到光波的相位差:

干涉条件:
干涉条纹的形成需要满足以下条件,即路径差对应的相位差应为整数倍的 2π:

其中,mm 是干涉级数(整数)。
3. 厚度的计算
从上述条件可以得到外延层的厚度公式:

其中:
m 是干涉条纹的级数(可以通过实验数据确定)
λ 是光波的波长(由波数计算得到)
n 是外延层的折射率
θ 是入射角
第一问优化:
1 选择干涉级数 m
干涉级数 m 对厚度的计算至关重要。通过分析实验数据中的干涉条纹(反射率曲线的变化),我们可以估算出 m 的值。通常通过反射率的峰值位置来判断不同的干涉级数。
2 折射率 n 的估算
折射率 nn 是外延层材料的性质之一。为了优化模型,我们可以通过实验数据或者查阅相关文献来估算 n 的值。如果 n 不随波长变化(即假设为常数),我们可以简化模型计算。
3优化反射率模型
根据附件提供的反射率数据,可以尝试拟合反射率与波数之间的关系.。

第二问
步骤 1:数据预处理
波数和波长的转换
反射率提取
步骤 2:干涉条纹检测
干涉条纹的周期检测
干涉级数 m的估计
步骤 3:折射率的估计
外延层的折射率 n 可能不是常数,而是随着波长变化的。通过实验数据或已有的材料数据(如文献中提供的碳化硅外延层的折射率模型)来估计折射率。
步骤 4:外延层厚度计算
根据反射率检测到的干涉条纹的位置、已知的入射角 θ 和估算的折射率 n,代入厚度公式 进行计算。
步骤 5:结果分析与可靠性
对多个数据点进行计算,得到一组外延层厚度的估计值。
分析结果的可靠性:可以通过交叉验证(例如,使用不同的入射角进行比较)来验证算法的稳定性和准确性。

第三问
问题 3 讨论的是多光束干涉的情况。我们需要推导产生多光束干涉的必要条件,并分析其对外延层厚度计算精度的影响。
- 多光束干涉原理
多次反射和透射:在外延层与衬底的界面之间,光波会多次发生反射和透射。每一次反射和透射都会引入新的光波,这些光波的相位差会导致干涉效应。
多光束干涉条件:要发生多光束干涉,反射光的路径差需要满足以下条件:每个反射光的路径差都是相同的,并且相位差应为 ( m .2Π )(其中 ( m ) 为整数)。这意味着每个光束在反射后与其他光束的路径差相同,并且产生相干干涉。 - 推导多光束干涉的必要条件
对于两次反射和透射的情况,光波的总路径差可以表示为:
![]()
在多次反射情况下,路径差会随着反射次数增加而变得更为复杂。如果考虑 ( n ) 次反射,路径差应为:
![]()
假设每次反射都会引入相位差,这些相位差的总和必须是整数倍的 ( 2\pi ) 才能形成干涉条纹。
- 多光束干涉对外延层厚度计算精度的影响
误差源:在多光束干涉情况下,每一束光的相位差会影响最终干涉条纹的位置。如果忽略了多光束的干涉效应,计算出的厚度可能会有系统性的偏差。特别是当反射次数较多时,这种影响会更加显著。
精度下降:如果只考虑一次反射和透射,可能会低估外延层厚度,因为没有考虑到反射光的多次干涉。因此,在高精度要求的情况下,需要考虑多光束干涉的影响,以提高计算精度。
其中更详细的思路、各题目思路、代码、讲解视频、成品论文及其他相关内容,可以点击下方群名片获取!
