当前位置：首页 > backend >正文

2020年_408统考_数据结构41题

backend 2025/9/5 16:45:26

题目

定义三元组 (a, b, c)（其中 a, b, c 均为正数）的距离 D = |a - b| + |b - c| + |c - a| 。给定 3 个非空整数集合 S1 、S2 和 S3 ，按升序分别存储在 3 个数组中。请设计一个尽可能高效的算法，计算并输出所有可能的三元组 (a, b, c)（a ∈ S1, b ∈ S2, c ∈ S3）中的最小距离。例如 S1 = {- 1, 0, 9} ，S2 = {-25, -10, 10, 11} ，S3 = {2, 9, 17 , 30, 41} ，则最小距离为 2 ，相应的三元组为 (9 , 10, 9) 。要求：

给出算法的基本设计思想。
根据设计思想，采用 C 或 C++ 语言描述算法，关键之处给出注释。
说明你所设计算法的时间复杂度和空间复杂度。

1.算法基本设计思想

先写出初始数组

在这里插入图片描述
D = |a - b| + |b - c| + |c - a|，这道题的最终结果就是求出 D 的最小值，不妨先画出数轴来帮助我们理解一下这到底是什么意思，这里以S1[2],S2[2],S3[0]为例：

红色代表S1, 绿色代表S2,蓝色代表S3
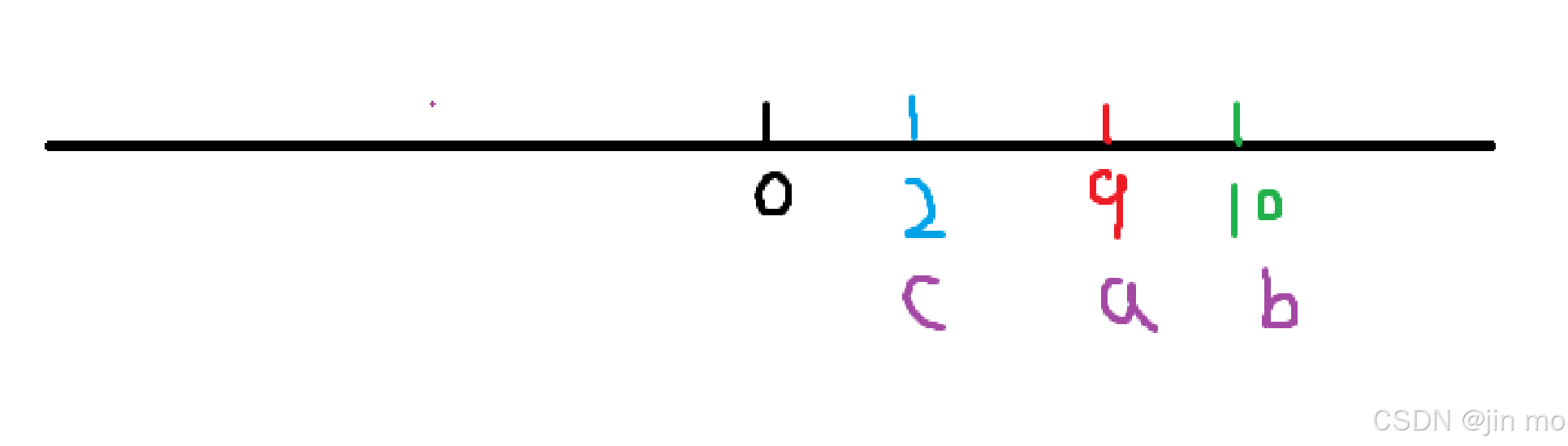
在这里插入图片描述

在这里插入图片描述
如图：开始推算，|a-b|=1 |b-c|=8 |c-a|=7 相加得出 d = 16,由此得出 D = (最右端 - 最左端 )*2,所以就要求左端点的值尽可能的大，右端点的值尽可能的小(由于数组是递增的，当前选定的右端点一定为最小值)，在数轴中小的数在最左边，所需要确认一个a,b,c中的最小值来做左端点，不断的去匹配，例如：
（题目中要求a,b,c大于0,我们示范时忽略这个条件）
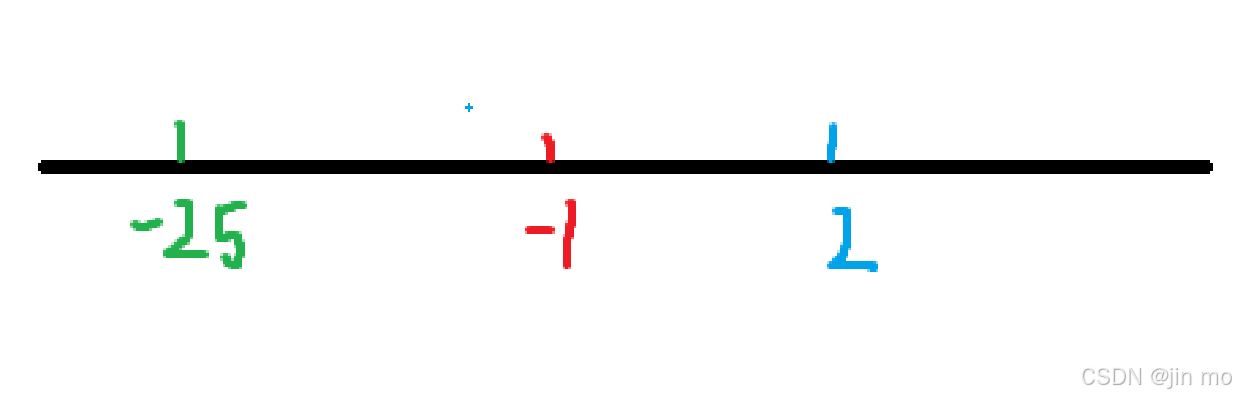
在这里插入图片描述
D=（2-（-25））*2 = 54
由于 a.b.c中 b的值最小，所以b做了左端点,继续匹配,b的值是当前的最小值(需要不断偏移左端点，使其变大)，存在于S2中，所以更改 b 为 -10

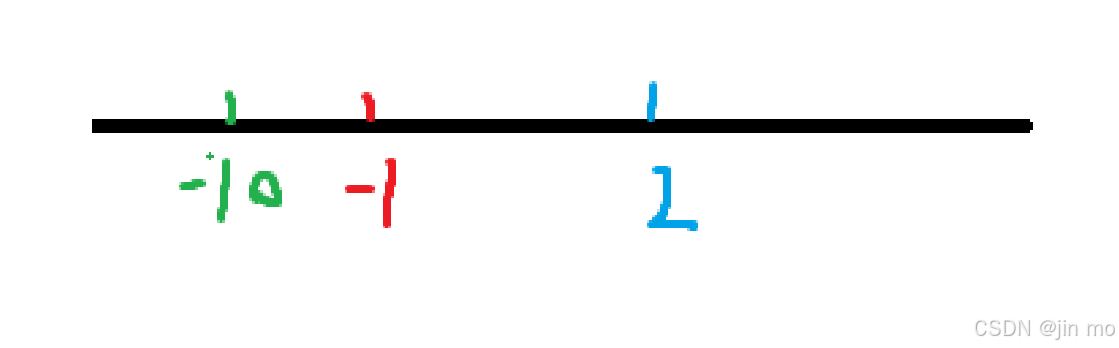
D=（2-（-10））*2 = 24

继续重复 ,更新b的值为10
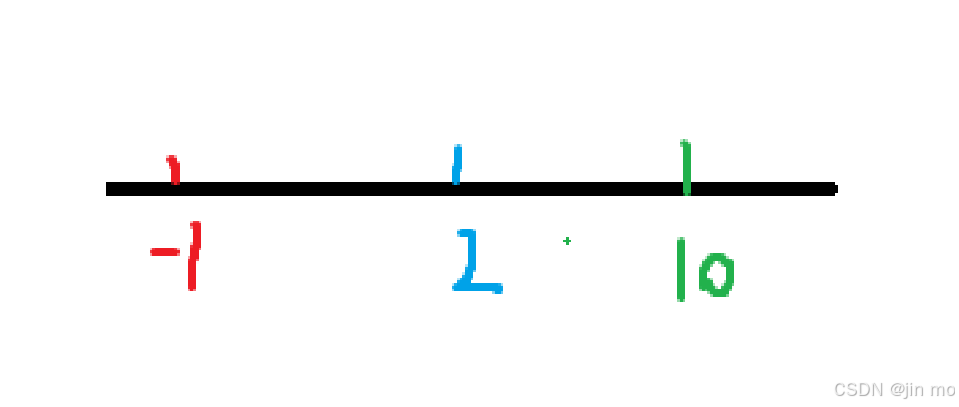
在这里插入图片描述
D=（10-（-1））* 2 = 22

此时，左端点变为了 a ，将其更新
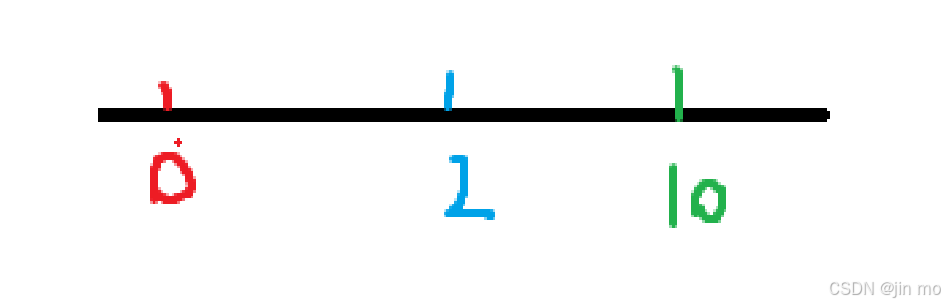
在这里插入图片描述
D=（10-0）*2 = 20

继续:
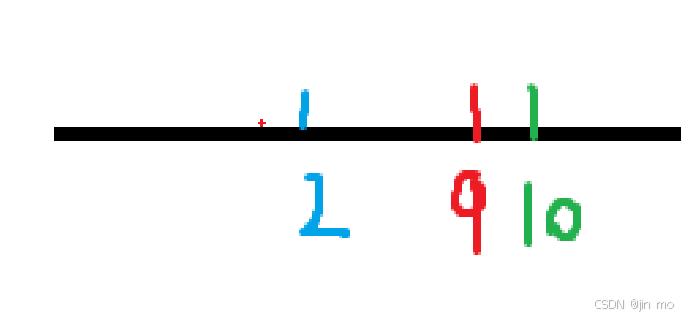
在这里插入图片描述
此时，左端点变为了 c ，更新：

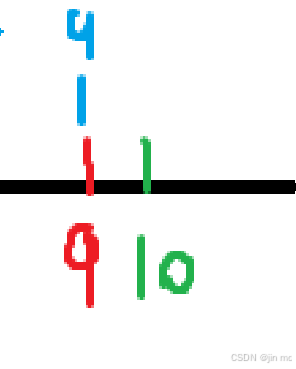
在这里插入图片描述
得出了答案，D=（10-9）*2此时继续更新，同时更新 a,c,发现 a 最高到 9 不能再向后偏移了，也就是说下次如果还是当前左端点最小的话，左端点的值就定死了，只能不断更新右端点（如果按照此例子来解释，就是当前a已经是 a,b,c中最小的了，由于数组是递增的，那么b和c之后的值一定会更大，不断的更新右端点）不断向前，最终导致D的值不断增大，继续移动 a 的指针会越界，因此只能移动其他最小值的指针，当至少有一个到达对应数组的末尾时，遍历必须终止：
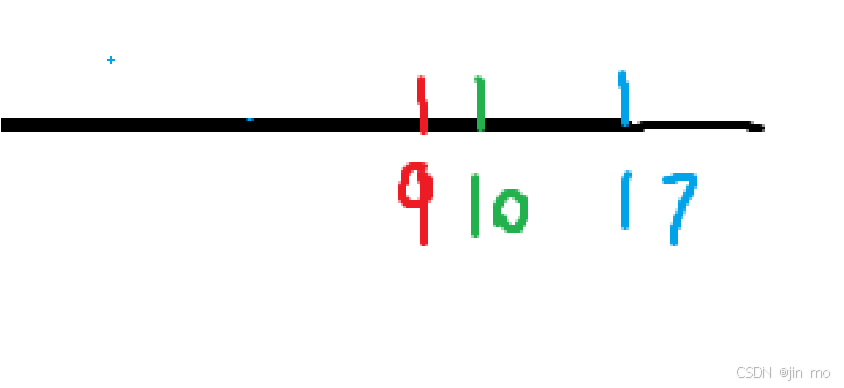
在这里插入图片描述
D=（17-9）*2 = 16

下来，根据数轴来推断，那么该如何将D变小呢？

推论

当：我们确定

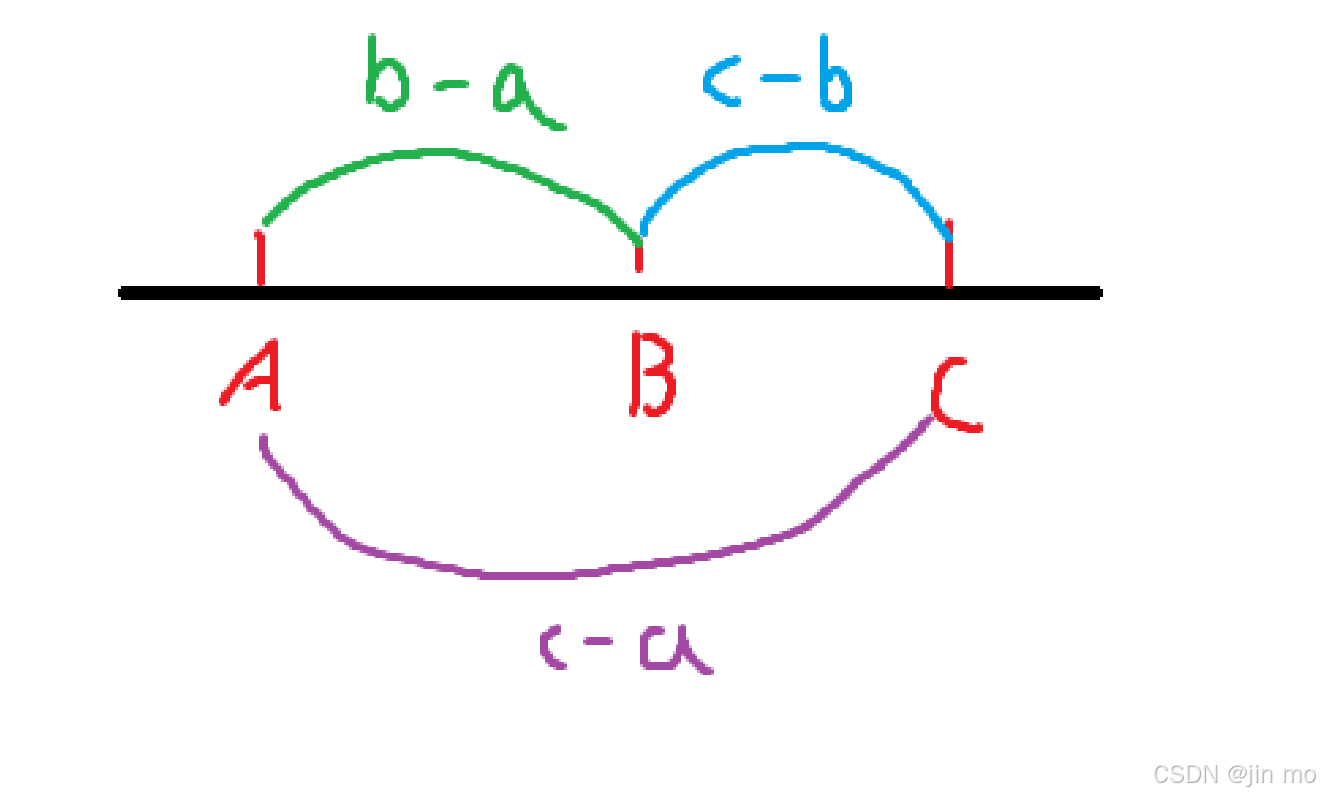
左端点朝右移，已知其余两个点的值，通过公式D = |a - b| + |b - c| + |c - a|
为什么知道其余两个点的值？
-当我们不断的移动当前 a (S1 [i])、b (S2 [j])、c (S3 [k]) 中的最小值，若最小值所在数组的指针未越界，则移动该指针，会出现三种情况
1. 更新的左端点的值还是最小值，其余两个点的值不变，由于数组递增，获取的新左端点一定比之前的左端点值大
2. 更新的左端点的值在原来右端点和当前左节点（已经替换）之间，当前左节点的值，在未更新前就已经知道，由于更新过后的左端点的值比原来左端点的值大，例如：

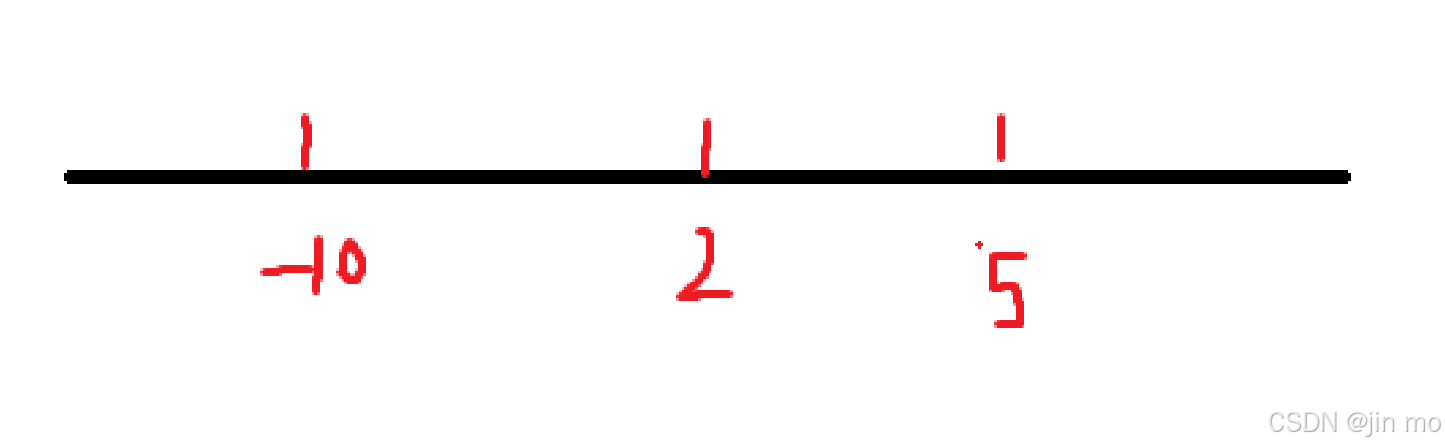
更新的左端点的值要在原来右端点和新的左端点（2）之间，所以取更新的左端点为 3

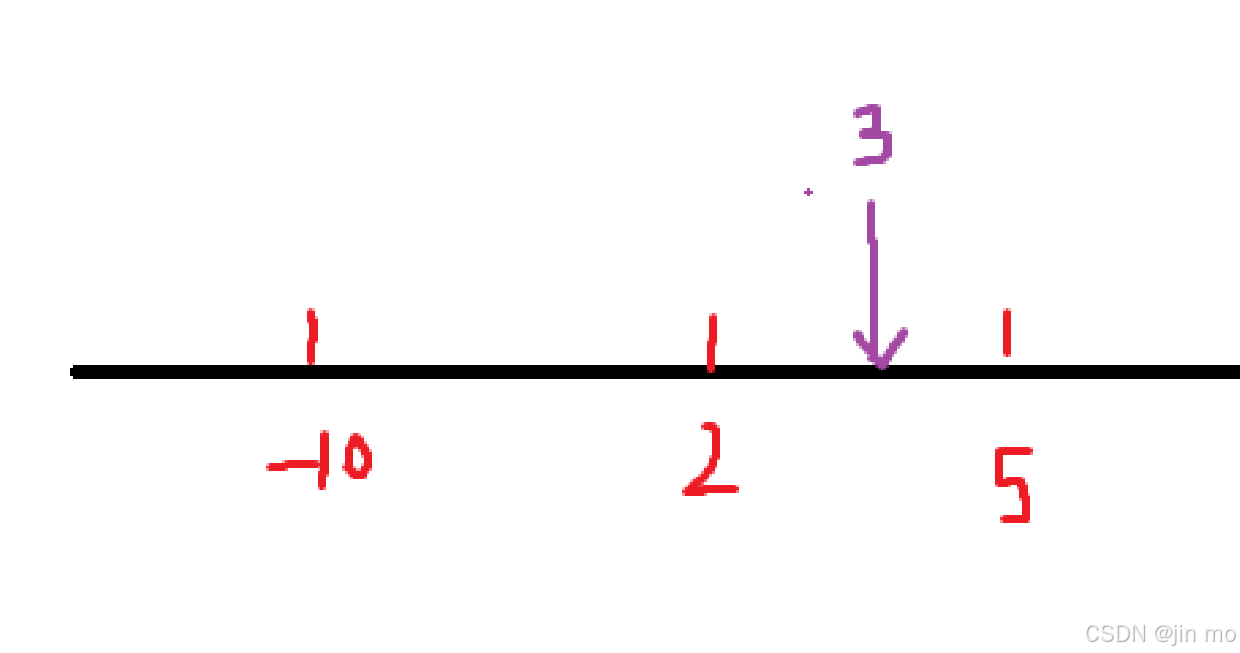
重新获取当前左端点，为 2 ，由此可知，获取的当前左端点的值一定是大于上一个左端点，但是右端点还是没有变，所以依旧可以确定三个点的位置，通过公式得出D依旧是减小的
3. 更新的左端点的值在原来右端点之后，如图;

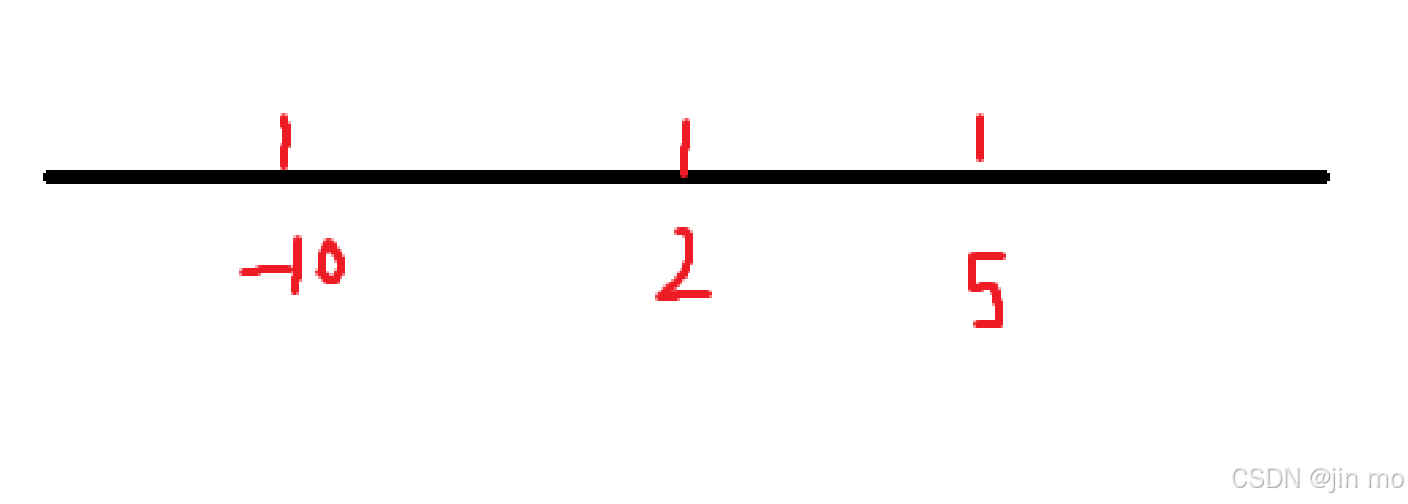
按照解释，更新的值应从 -10 更新为大于 5 的值
- 如果更新的值等于 17（5+2+10），那么D值不变
- 如果更新的值小于 17 ，那么D值减小
- 如果更新的值大于 17 ，那么D的值增大
我们每次计算D的之后，都会令其和之前的D比较，发现小于之前的D，更新答案，就避免了这种，还没有遍历完D就增大的情况

算法思路

通过遍历数组，从 0 索引开始，同时获取S1，S2, S3的元素，通过不断的比较，来确定左端点，然后不断的更新最小的数，不断更新左节点，不断的计算D，以获得最终答案

代码实现;

/*************************************************************************> File Name: solve.cpp> Author:> Mail:> Created Time:************************************************************************//************************************************************************** 题目：计算三个有序数组中元素组成的三元组的最小距离* 算法思路：* 1. 利用三指针法遍历三个有序数组* 2. 每次计算当前三个元素的距离 D = |a-b| + |b-c| + |c-a|* 3. 选择三个元素中最小的那个元素，前进其所在数组的指针* 4. 重复上述过程直到任一数组遍历完毕* 5. 在整个过程中记录最小距离************************************************************************/
#include <iostream>
#include <cstdlib>
#include <queue>
using namespace std;int min_num(int a, int b, int c) {if (a > b) swap(a, b);if (a > c) swap(a, c);return a;
}int func(queue<int> que1, queue<int> que2, queue<int> que3) {int ans = 0x3f3f3f3f;//设置answhile (!que1.empty() && !que2.empty() && !que3.empty()){int a = que1.front(), b = que2.front(), c = que3.front();int D = abs(a - b) + abs(b - c) + abs(c - a);ans = min(ans, D);int new_left = min_num(a, b, c);if (a == new_left) que1.pop();if (b == new_left) que2.pop();if (c == new_left) que3.pop();//操作完毕之后已经获得了最新的指针位置}return ans;
}int main() {int m, n, k, x;queue<int> que1, que2, que3;cin >> m >> n >> k;for (int i = 0; i < m; i++) {cin >> x;que1.push(x);}for (int i = 0; i < n; i++) {cin >> x;que2.push(x);}for (int i = 0; i < k; i++) {cin >> x;que3.push(x);}cout << func(que1, que2, que3) << endl;return 0;
}