当前位置：首页 > backend >正文

力扣hot100 | 堆 | 215. 数组中的第K个最大元素、347. 前 K 个高频元素、128. 最长连续序列

backend 2025/9/2 8:18:59

215. 数组中的第K个最大元素

力扣题目链接
给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5

示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

一、暴力解法【能通过但不满足题目要求】

【思路】排序后选倒数第k个就是第k大的。

class Solution:def findKthLargest(self, nums: List[int], k: int) -> int:return sorted(nums)[-k] # -k这种写法居然是合法的。。。# 或者：# nums.sort(reverse = True)# return nums[k - 1]

时间复杂度 O(n log n)：Timsort本质上是归并排序的改进版本，当数据是随机的（没有明显的有序模式）时，它的行为接近标准归并排序。
空间复杂度 O(1)

补充：归并排序的复杂度推导

分治思想：T(n) = 2T(n/2) + O(n), 其中：

2T(n/2)：将数组分成两半，分别排序
O(n)：合并两个已排序的子数组

递归树分析:

第0层: T(n)                    工作量: n
第1层: 2×T(n/2)               工作量: n
第2层: 4×T(n/4)               工作量: n
...
第k层: 2^k×T(n/2^k)          工作量: n

树的深度：k = log₂(n)、每层的工作量都是O(n)
所以总时间复杂度：O(n) × O(log n) = O(n log n)

二、快速选择

此方法参考自：Krahets。

快速排序的核心包括“哨兵划分” 和 “递归” 。

哨兵划分：以数组某个元素（一般选取首元素）为基准数，将所有小于基准数的元素移动至其左边，大于基准数的元素移动至其右边。
递归：对左子数组和右子数组递归执行哨兵划分，直至子数组长度为 1 时终止递归，即可完成对整个数组的排序。

下图展示了数组 [2,4,1,0,3,5] 的快速排序流程。
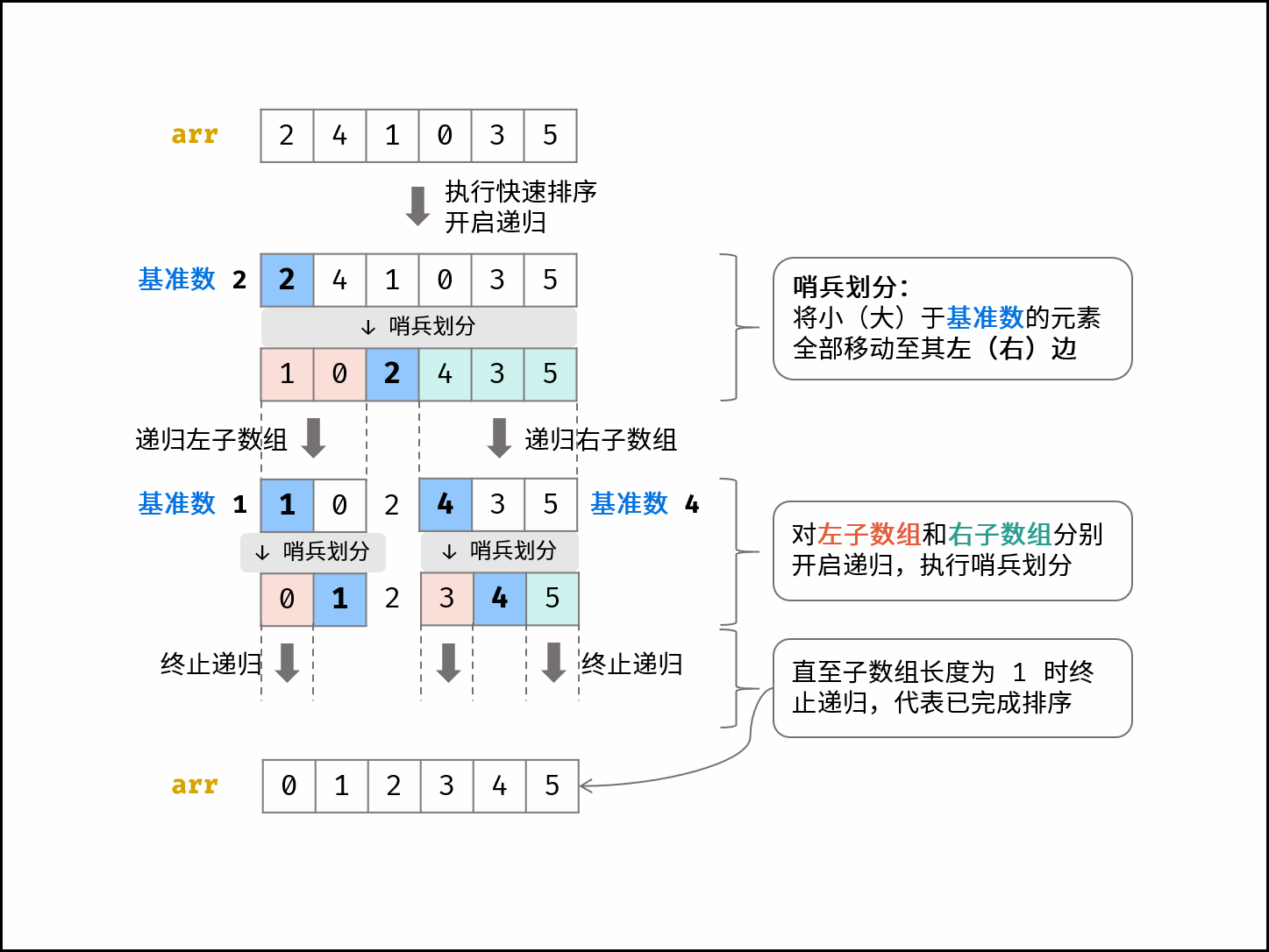
在这里插入图片描述

「快速选择」：设 n 为数组长度。根据快速排序原理，如果某次哨兵划分后，基准数的索引正好是 n-k ，则意味着它就是第 k 大的数字。此时就可以直接返回它，无需继续递归下去了。

然而，对于包含大量重复元素的数组，每轮的哨兵划分都可能将数组划分为长度为 1 和 n−1 的两个部分，这种情况下快速排序的时间复杂度会退化至 O( $n^2$ ) 。

一种解决方案是使用 「三路划分」，即每轮将数组划分为三个部分：小于、等于和大于基准数的所有元素。这样当发现第 k 大数字处在“等于基准数”的子数组中时，便可以直接返回该元素。

为了进一步提升算法的稳健性，我们采用随机选择的方式来选定基准数。

class Solution:def findKthLargest(self, nums: List[int], k: int) -> int:def quick_select(nums, k):pivot = random.choice(nums) # 随机选择基准数# 将大于、小于、等于 pivot 的元素划分至 big, small, equal 中big, equal, small = [], [], []for num in nums:if num > pivot:big.append(num)elif num < pivot:small.append(num)else:equal.append(num)if k <= len(big):  # 第 k 大元素在 big 中，递归划分return quick_select(big, k)if len(nums) - len(small) < k: # 第 k 大元素在 small 中，递归划分return quick_select(small, k - len(nums) + len(small))return pivot  # 第 k 大元素在 equal 中，直接返回 pivotreturn quick_select(nums, k)

时间复杂度 O(n) ：其中 n 为数组元素数量。
- 对于长度为 n 的数组执行哨兵划分操作的时间复杂度为 O(n)。
- 每轮哨兵划分后，向下递归子数组的平均长度为 $n2\frac{n}{2}$ 。
- 因此平均情况下，哨兵划分操作一共有 $\frac{n}{2} + \frac{n}{4} + ...+ \frac{n}{n} = \frac{n-\frac{1}{2}}{1-\frac{1}{2}} = 2n - 1$ （等比数列求和），复杂度为 O(n) 。
空间复杂度 O(logn) ：划分函数的平均递归深度为 O(logn)。

347. 前 K 个高频元素

力扣题目链接
给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1：
输入：nums = [1,1,1,2,2,3], k = 2
输出：[1,2]

示例 2：
输入：nums = [1], k = 1
输出：[1]

示例 3：
输入：nums = [1,2,1,2,1,2,3,1,3,2], k = 2
输出：[1,2]

进阶：你所设计算法的时间复杂度必须优于 O(n log n) ，其中 n 是数组大小。

桶排序

参考自：灵茶山艾府

【思路】创建一个Counter字典，再转成一个 “桶列表” buckets[c] 存储出现次数为 c 的元素们。（每个 buckets[c] 都是一个列表），再倒序遍历。
【步骤】
1. 用一个哈希表 cnt 统计每个元素的出现次数。哈希表的 key 是元素值，value 是相应出现次数。
2. 设出现次数最大值为 maxCnt，由于 maxCnt ≤ n，我们可以用桶排序，把出现次数相同的元素，放到同一个桶中（二维列表的同一个位置）：
  创建一个大小为 maxCnt+1 的列表 buckets，其中 buckets[c] 存储出现次数为 c 的元素。（每个 buckets[c] 都是一个列表）、遍历 cnt，把出现次数为 c 的元素 x 添加到 buckets[c] 中。
3. 倒序遍历 buckets，把 buckets[c] 中的元素加到答案中。一旦答案的长度等于 k，就立刻返回答案。

from collections import Counter
class Solution:def topKFrequent(self, nums: List[int], k: int) -> List[int]:# e.g. [1, 3, 2, 2, 1] ——> {1:2, 2:2, 3:1} ——> [[], [3], [1,2]]# 1. 统计每个元素的出现频次 cnt = Counter(nums)max_cnt = max(cnt.values()) # 最大频次——用来计算需要多少个桶# 2. 把出现次数相同的元素，放到同一个桶中（同一位置上）buckets = [[] for _ in range(max_cnt + 1)]# 【常见陷阱！】buckets = [[]] * (max_cnt + 1)for x, c in cnt.items():buckets[c].append(x) # 3. 倒序遍历buckets, 把出现次数前 k 大的元素加入答案res = []for bucket in reversed(buckets):# 列表的+操作 将两个列表按顺序连接起来（concatenate）res += bucket # [a, b] + [x, y] = [a, b, x, y]if len(res) == k: # 注意题目保证答案唯一，一定会出现恰好等于 k 的情况return res

时间复杂度 O(n)
空间复杂度 O(n)

【注意】初始化桶列表时不能`buckets = [[]] * (max_cnt + 1)`！！

核心原则：可变 vs 不可变对象

对象类型	示例	`[obj] * n` 是否安全	原因	推荐做法
不可变对象	`int`, `str`, `tuple`, `bool`, `None`	✅ 安全	修改时是替换引用，不影响其他位置	直接使用乘法
可变对象	`list`, `dict`, `set`, 自定义类实例	❌ 危险	所有位置共享同一个对象引用	使用列表推导式

✅ 安全的写法（不可变对象）

写法	结果	修改后	说明
`[0] * 5`	`[0, 0, 0, 0, 0]`	`arr[0] = 10` → `[10, 0, 0, 0, 0]`	数字不可变，安全
`[None] * 3`	`[None, None, None]`	`arr[1] = 'hello'` → `[None, 'hello', None]`	None不可变，安全
`[''] * 4`	`['', '', '', '']`	`arr[0] = 'hi'` → `['hi', '', '', '']`	字符串不可变，安全
`[False] * 3`	`[False, False, False]`	`arr[2] = True` → `[False, False, True]`	布尔值不可变，安全

❌ 危险的写法（可变对象）

错误写法	正确写法	问题演示
`[[]] * 3`	`[[] for _ in range(3)]`	`arr[0].append(1)` → `[[1], [1], [1]]` 😱
`[{}] * 2`	`[{} for _ in range(2)]`	`arr[0]['key'] = 'value'` → 所有字典都被修改
`[set()] * 4`	`[set() for _ in range(4)]`	`arr[0].add(1)` → 所有集合都被修改
`[[0] * 2] * 3`	`[[0] * 2 for _ in range(3)]`	`arr[0][0] = 5` → 所有子列表都被修改

295. 数据流的中位数

力扣题目链接
中位数是有序整数列表中的中间值。如果列表的大小是偶数（没有中间值），则中位数是两个中间值的平均值。

例如 arr = [2,3,4] 的中位数是 3 。
例如 arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。

实现 MedianFinder 类:

MedianFinder() 初始化 MedianFinder 对象。
void addNum(int num) 将数据流中的整数 num 添加到数据结构中。
double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 $10^{-5}$ 以内的答案将被接受。

示例 1：
输入
[“MedianFinder”, “addNum”, “addNum”, “findMedian”, “addNum”, “findMedian”]
[[], [1], [2], [], [3], []]
输出
[null, null, null, 1.5, null, 2.0]
解释
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1); // arr = [1]
medianFinder.addNum(2); // arr = [1, 2]
medianFinder.findMedian(); // 返回 1.5 ((1 + 2) / 2)
medianFinder.addNum(3); // arr[1, 2, 3]
medianFinder.findMedian(); // return 2.0

一、暴力法

法一：
- 添加元素时直接append插入列表中O(1)；
- 找中位数时O(n log n)【先排序O(n log n)、再返回中间元素O(1)】；
法二：
- 在添加元素时保持数组有序O(n)【用二分查找元素插入位置 O(logn) 、向数组某位置插入元素 O(n) （插入位置之后的元素都需要向后移动一位）】
- 取中位数时只需要返回中间元素O(1)；
【都不推荐】

二、大顶堆 + 小顶堆【推荐】

参考自：Krahets

建立一个小顶堆 A 和大顶堆 B ，各保存列表的一半元素，且规定：
- A 保存较大的一半，长度为 $N2\frac{N}{2}$ （ N 为偶数）或 $N+12\frac{N+1}{2}$ （ N 为奇数）。
- B 保存较小的一半，长度为 $N2\frac{N}{2}$ （ N 为偶数）或 $N−12\frac{N-1}{2}$ （ N 为奇数）。
随后，中位数可仅根据 A,B 的堆顶元素计算得到。

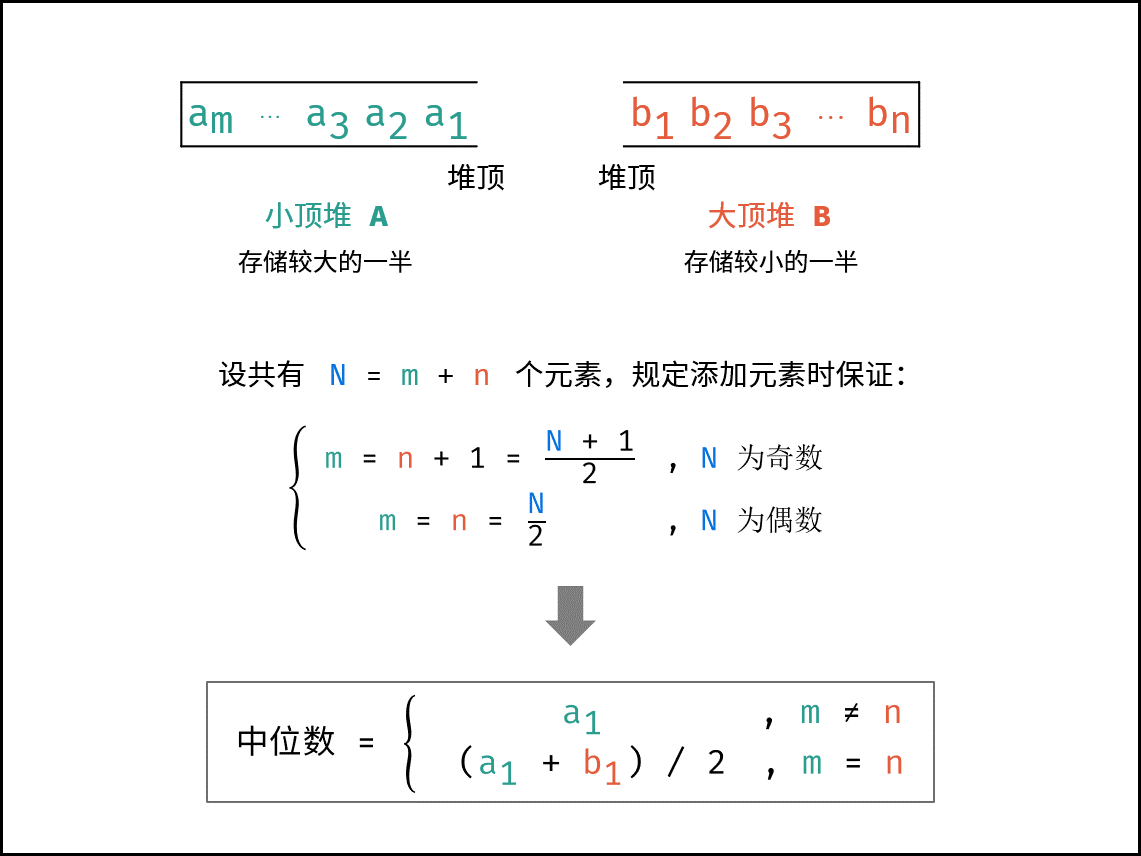
在这里插入图片描述

【步骤】设元素总数为 N=m+n ，其中 m 和 n 分别为 A 和 B 中的元素个数。
- 函数 addNum(num) ：
  1. 当 m = n（即 N 为偶数）：需向 A 添加一个元素 —— 实现方法：将新元素 num 插入至 B ，再将 B 堆顶元素插入至 A 。
  2. 当 m!=n（即 N 为奇数）：需向 B 添加一个元素 —— 实现方法：将新元素 num 插入至 A ，再将 A 堆顶元素插入至 B 。
  假设插入数字 num 遇到情况 1. 。由于 num 可能属于 “较小的一半” （即属于 B ），因此不能将 nums 直接插入至 A 。而应先将 num 插入至 B ，再将 B 堆顶元素插入至 A 。这样就可以始终保持 A 保存较大一半、 B 保存较小一半。
- 函数 findMedian() ：
  1. 当 m=n（ N 为偶数）：则中位数为 $(A 的堆顶元素 + B 的堆顶元素) /2$ 。
  2. 当 m!=n（ N 为奇数）：则中位数为 $A 的堆顶元素$ 。
【代码实现】Python 中 heapq 模块是小顶堆。实现 大顶堆 方法：小顶堆的插入和弹出操作均将元素 取反号 即可。

from heapq import *class MedianFinder:def __init__(self):self.A = [] # 小顶堆，保存较大的一半self.B = [] # 大顶堆，保存较小的一半def addNum(self, num: int) -> None:if len(self.A) != len(self.B):heappush(self.A, num)heappush(self.B, -heappop(self.A))else:heappush(self.B, -num)heappush(self.A, -heappop(self.B))def findMedian(self) -> float:return self.A[0] if len(self.A) != len(self.B) else (self.A[0] - self.B[0]) / 2.0

Push item on the heap, then pop and return the smallest item from the heap. The combined action runs more efficiently than heappush() followed by a separate call to heappop().

可优化为以下写法【合起来写跑得更快】：

from heapq import *class MedianFinder:def __init__(self):self.A = [] # 小顶堆，保存较大的一半self.B = [] # 大顶堆，保存较小的一半def addNum(self, num: int) -> None:if len(self.A) != len(self.B): # 先push进A，再pop A顶进Bheappush(self.B, -heappushpop(self.A, num)) # 注意入B的要取反号！else:heappush(self.A, -heappushpop(self.B, -num)) # 注意出B的也要取反号！def findMedian(self) -> float:return self.A[0] if len(self.A)!=len(self.B) else (self.A[0] - self.B[0])/2  # 注意这里B[0]也要取反！！中间不是+！！

时间复杂度 O(logN) ：
- 查找中位数 O(1) ：获取堆顶元素使用 O(1) 时间。
- 添加数字 O(logN) ：堆的插入和弹出操作使用 O(logN) 时间。
空间复杂度 O(N) ：其中 N 为数据流中的元素数量，小顶堆 A 和大顶堆 B 最多同时保存 N 个元素。
【注意】写法heappushpop()是push在前pop在后！！【先push再pop是符合顺序的！】
【注意】始终要记得B的出入元素都要取反号！三行核心代码中都要牢记这一点！！！