当前位置：首页 > backend >正文

神经网络1——sklearn的简单实现

backend 2025/9/2 7:52:31

神经网络是指一种特定类型的假设函数，它由多个参数化、可微分的函数组合而成，用于形成输出。神经网络是深度学习的核心。它们用途广泛、功能强大且可扩展，使其非常适合处理大型和高度复杂的机器学习任务。
例如对数十亿个图像进行分类（例如Google Images），为语音识别服务提供支持，每天向成千上万的用户推荐（例如抖音）观看的最佳视频，或学习在围棋游戏（DeepMind的AlphaGo）中击败世界冠军。

一、神经网络的发展过程

1、启蒙与雏形

人工神经网络已经存在很长一段时间了：它们于1943首次提出，该模型计算了生物神经元如何在动物大脑中协同工作，利用命题逻辑进行复杂的计算。这是第一个人工神经网络架构（MP模型），该神经元接收二进制信号（0或1），进行加权求和，然后通过一个阈值函数（Step Function）输出。他们甚至证明了这种简单的网络可以模拟基本的逻辑运算。从那时起，许多其他架构被发明出来。

赫布法则：“一起激发的神经元连接在一起”。通俗讲，如果两个神经元总是同时被激活，那么它们之间的连接强度（权重）就应该增强。这为后来的监督学习（如梯度下降）提供了生物学灵感。

2、第一次兴衰

人工神经网络的早期成功（感知机模型的出现）导致人们普遍相信，我们很快将与真正的智能机器进行对话。当在20世纪60年代人们清楚地知道不能兑现这一承诺（至少相当长一段时间）时，资金流向了其他地方，人工神经网络进入了漫长的冬天。

感知机模型：第一个可以用算法学习权重（通过调整权重来减少错误）的神经网络模型，并做出硬件实现。本质上是一个单层的MP模型，用于二分类，但是单层的感知机无法解决线性不可分问题（如下图，不管用哪个决策线都会有1/3的分类错误），陷入低谷。

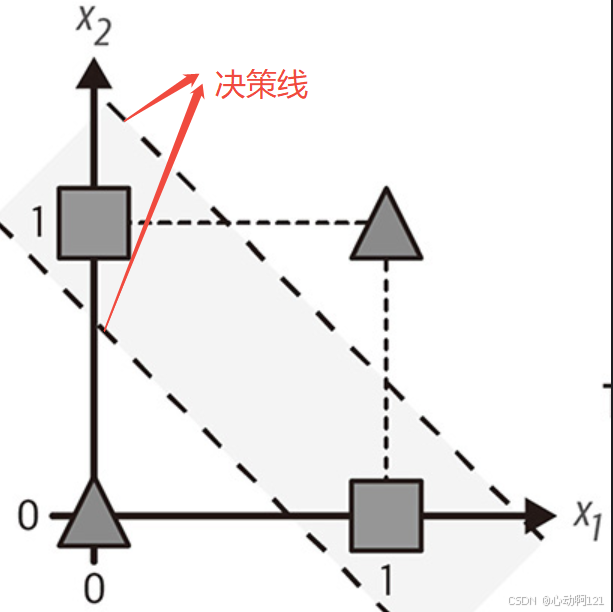
3、复兴与BP算法的传播

在20世纪80年代初期，发明了新的架构（反向传播算法），并开发了更好的训练技术，从而激发了人们对连接主义（神经网络的研究）的兴趣。但是进展缓慢。

反向传播算法（简称：BP算法），通过链式法则，将输出层的误差反向传播到网络额每一层，从而指导各层权重的调整。

4、第二次兴衰

到了20世纪90年代，发明了其他强大的机器学习技术，例如支持向量机。这些技术提供了似乎比人工神经网络更好的结果和更坚实的理论基础，神经网络的研究再次被搁置。

问题：算力不足，巨大的计算资源和数据使用当时的硬件无法满足

梯度消失/爆炸：在训练深度网络的时候BP算法的梯度会随着层数的增加而急剧缩小或增大，导致无法有效学习

强大的竞争对手（支持向量机），其他的机器学习在这一时期占据主流

5、深度学习革命

现在目睹了对人工神经网络的另一波兴趣。这波浪潮会像以前一样消灭吗？这里有一些充分的理由使我们相信这次是不同的，人们对人工神经网络重新充满兴趣将对我们的生活产生更深远的影响：

现在有大量数据可用于训练神经网络，并且在非常大和复杂的问题上，人工神经网络通常优于其他机器学习技术。——大数据
自20世纪90年代以来，计算能力的飞速增长使得现在有可能在合理的时间内训练大型神经网络。这部分是由于摩尔定律（集成电路中的器件数量在过去的50年中，每两年大约增加一倍）这还要归功于游戏产业，它刺激了数百万计强大的GPU卡的生产。此外，云平台已使所有人都可以使用这个功能。——强算力
训练算法已得到改进。它们与20世纪90年代使用的略有不同，但是这些相对较小的调整产生了巨大的积极影响。——新算法
在实践中，人工神经网络的一些理论局限性被证明是良性的。例如，许多人认为ANN训练算法注定要失败，因为它们可能会陷入局部最优解，但事实证明这在实践中并不是一个大问题，尤其是对于较大的神经网络：局部最优解通常表现得几乎与全局最优解一样好。
人工神经网络似乎已经进入了资金和发展的良性循环。基于人工神经网络的好产品会成为头条新闻，这吸引了越来越多的关注和资金，从而带来了越来越多的进步甚至产生了惊人的产品。

二、最简单的神经网络架构感知机

感知机称为阈值逻辑单元（Threshold Logic Unit LTU）,有时也称为线性阈值（Linear Threshold Unit ,LTU）。输入和输出是数字（而不是二进制开/关值）,并且每个输入连接都与权重相关联。

1、单层感知机（用于二分类，SLP）

（1）单输出感知机

首先，计算输入的线性函数： $z = w_1 x_1 + w_2 x_2 + \dots + w_n x_n + b = \mathbf{w}^T \mathbf{x} + b$

其次，对线性函数结果应用阶跃函数：

$h_w(x) = \text{step}(z) =heaviside(z) = \begin{cases} 0 , z<0 \\ 1 ,z\geqslant 0 \end{cases}$ 或 $step(z) = sgn(z)= \begin{cases} -1 ,z<0 \\ 0 \, \, \, \, ,z=0 \\ 1\, \, \, \, ,z>0 \end{cases}$ ，这两个是常见的阶跃函数。

最后，输出阶跃函数得到的值，这个就是单个LTU。如下图：

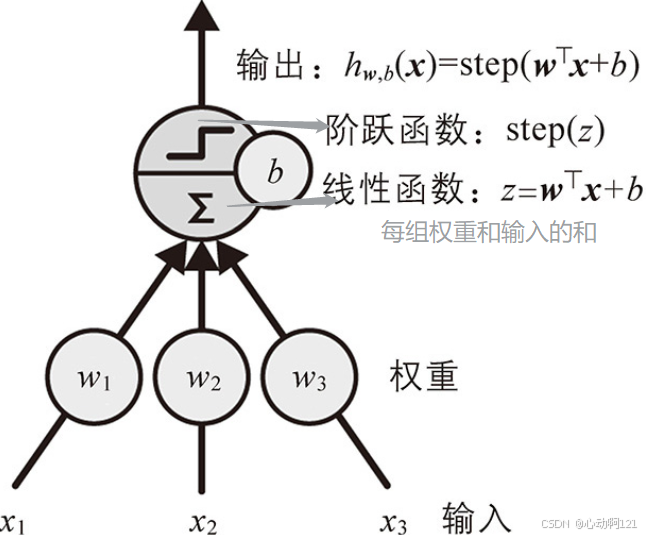
（2）多输出感知机

感知机由一个或多个组织在单层的TLU组成，其中每个TLU都连接到每个输入。这样的层称为全连接层（或密集层）；这些输入构成输入层。最终由TLU层产生最终输出。有几个输出就是几个标签分类器。

全连接输出的核心思想是：感知机的每个输出都与其每个权重连接，没有遗漏。

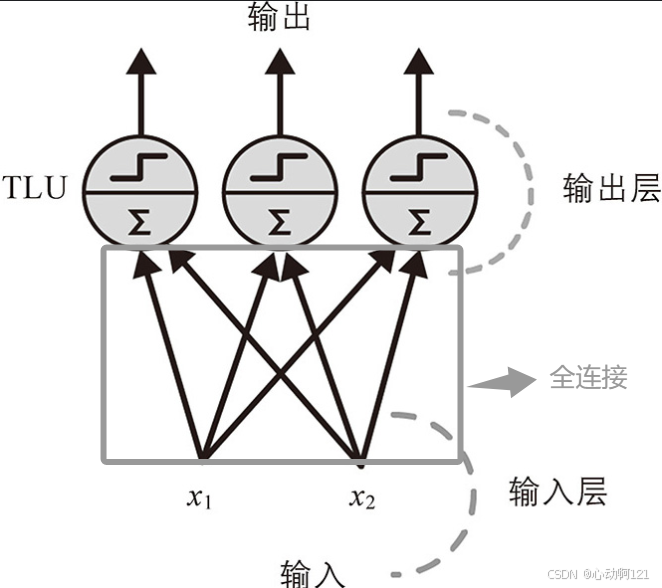
计算全连接： $h_{w,b}(X) = \Phi (XW+b)$

X：代表输入特征的矩阵，每个实例一行，每个特征一列

W：权重矩阵，每个输出一行，每个神经元一列

b：偏置向量：每个神经元一个

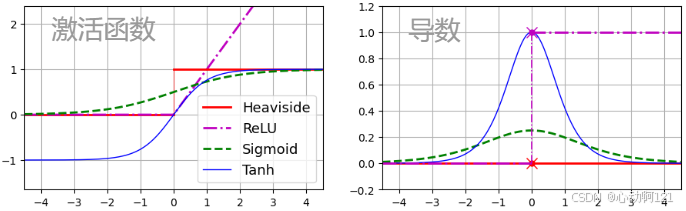
函数 $\Phi$ 为激活函数：当神经元是TLU时，它时阶跃函数。

感知机一次被送入一个训练实例，并且针对每个实例进行预测，对于产生错误预测的每个输出神经元，它会增强来自输入的连接权重，有助于正确的预测。

感知机权重更新： $w_{i,j} = w_{i,j}+\eta (y_i-\widehat{y_i})x_i$

$w_{i,j}$ ：第 i 个输入和第 j 个神经元之间的连接权重

$x_i$ ：当前实例的第 i 个输入值

$\widehat{y_i}$ ：当前实例的第 j 个输出神经元的输出

$y_i$ ：当前实例的第 j 个输出神经元的目标输出

$\eta$ ：学习率

每个输出神经元的决策边界都是线性的，因此感知机无法学习复杂的模型；如果训练实例时线性可分离的，这个算法会收敛到一个解。

# 练习：使用 numpy 实现感知机的训练
import numpy as np
def heaviside(z):return np.where(z >= 0, 1, 0)class gzj:def __init__(self, alpha=1, max_iter=100):self.alpha = alpha  # 学习率self.max_iter = max_iter  # 最大迭代次数def fit(self,X,y):self.w = np.random.randn(X.shape[1])self.b = np.random.rand()for _ in range(self.max_iter):for i in range(X.shape[0]):y_real = y[i]y_pred = heaviside(np.dot(X[i], self.w) + self.b)self.w = self.w + self.alpha * (y_real - y_pred) * X[i]self.b = self.b + self.alpha * (y_real - y_pred)return selfdef predict(self,X):return X @ self.w + self.b >=0

2、多层感知机（MLP）

单层感知机有严重缺陷，特别是他们无法解决一些微不足道的问题（异或分类问题）。任何其他线性分类模型都是如此。

可以通过堆叠多个感知机来消除感知机的局限性，这个就是多层感知机（神经网络最基础的形式）。

多层感知机：一个输入层，一个或多个隐藏层，一个输出层

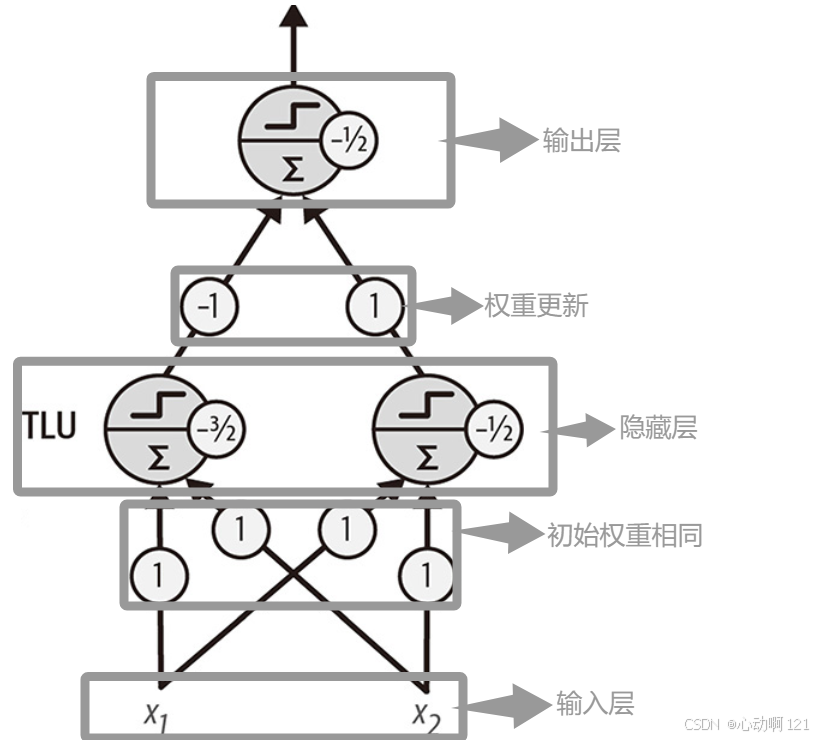
用代码实现上图中的过程：

import numpy as npdef step(z):  # 阶跃函数return np.where(z >= 0, 1, 0)def mlp_xor(X):w1 = np.ones((2,2))b1 = np.array([-1.5,-0.5])z1 = step(X@w1+b1)w2 = np.array([-1,1]).reshape(2,1)b2 = -0.5y = step(z1@w2+b2)return y
# 测试 4 个输入
X = np.array([[0,0],[1,0],[0,1],[1,1]])
print("X:\n", X)
print("XOR:\n", mlp_xor(X))  # 期望 [0,1,1,0]

3、sklearn神经网络

前馈神经网络：单项生产流水线，从输入到输出沿一个方向流动，没有循环和反馈连接。

深度神经网络：当神经网络包含一个深层的隐藏层时，就可以叫做深度神经网络。

函数逼近核心思想：找到一个函数尽可能的描述数据点背后的隐藏规律。

神经网络的函数逼近：神经网络理论上可以以任意高的精度来近似任何一个复杂的、未知的函数。

（1）MLP的理论计算

训练多层感知机时，目标是最小化损失函数 $L(\widehat{y},y)$ ，并求解各层参数（权重和偏置）的梯度，以便进行梯度下降更新。

数值微分 —— 符号法 —— 反向传播（初始化梯度；反向迭代）

数值微分：对每个参数，用有限差分近似（ $\frac{\partial f}{\partial w} \approx \frac{f(w + \epsilon) - f(w)}{\epsilon}$ ）

优点：思路直观，易于理解

缺点：计算开销极大（网络有成千上万的参数就需要成千上万次函数计算）；不准确（有限差分引入截断误差和舍入误差）；不可扩展（深度神经网络中完全不现实）

符号法：对网络的计算公式逐层写出，之后按照链式法则手工推导每个参数的偏导数。

优点：能够得到精确的解析梯度，没有数值误差；数学上严谨

缺点：枯燥繁琐（网络层数一多，公式就会爆炸式增长）；容易出错（人工推导常常漏项或符号错误）；难以通用（每换一个网络结构，都要重新手工推导一遍，无法转化通用程序）

反向传播：用统一的矩阵运算，把梯度传播过程高效、程序化地实现。

反向传播实现过程	含义
前向传播1： $Z_1 = X$	初始化输出（开始为输入内容）
前行传播2： $A_i = Z_iW_i +b_i \\ Z_{i+1} = sigmoid(A_i)$	迭代每层的输出值 $Z_{i+1}$ 和激活函数之前的函数 $A_i$ 这里权重是随机初始化的，这样能够破坏神经网络的对称性，从而实现每个神经元的独特性。（神经元如果保持对称性，那么训练会失败）这里的阶跃函数改成sigmoid函数，是因为阶跃函数无法进行梯度计算（梯度处处为0），sigmoid函数是光滑的、连续的曲线，它在所有点上都有非零的、易于计算的导数。另外两个受欢迎的函数： $tanh(z) = 2sigmoid(2z)-1$ （双曲正切函数为：S型，输出范围-1~1，能够加快收敛速度）， $ReLU(z)= max(0,z)$ （线性整流单元函数，运行良好且计算快因此为默认值，有助于减少梯度下降遇到的问题）
反向传播1： $G_{L+1} = (\widehat{y}-y)/m$ ，m是样本数量	初始化输出梯度 $\widehat{y}-y$ ：是损失值对预测值的导数，反应了预测值应该朝哪个方向移动，移动多大距离。 /m：表示的是求平均梯度
反向传播2： $\delta_i = G_{i+1} \cdot {Sigmod}'(A_i)$	计算每层的误差：调整方向 ✖ 调整A的效率
反向传播3： $w_i = Z^T_i \delta _i \\ b_i = 1^T \delta _i$ 1是m行1列的	计算每层的梯度：输入值 ✖ 每层误差注意：前向传播的时候 $Z_{i+1}$ 是本层的输出，这里的 $Z_i$ 是本层的输入
反向传播4 ： $G_i = \delta _i W^T_i$	传回上一层梯度

反向传播的工作流程：

一次处理一个小批量，并且多次遍历整个训练集，每次遍历都被称为一个轮次。

每个小批量通过输入层进入网络。之后该算法为小批量中的每个实例计算第一个隐藏层中所有神经元的输入。结果传递到下一层，以此类推，知道最有一层的输出，这就是前向传递。在前向传递的收保留所有的中间结果，因为反向传递会需要它们。

接下来，该算法测量网络的输出误差（使用损失函数，将期望输出与实际输出进行比较，并返回误差测量值）

然后，计算每个输出偏置和到输出层的每个连接对误差的贡献程度。（通过链式法则进行分析）

之后，该算法再次使用链式法则测量这些误差贡献中有多少来自下层中的每个连接，直到到达输入层为止。

最后，该算法执行梯度下降步骤，使用更改计算出的误差梯度来调整网络中所有连接权重。

（2）MPL回归

MLP可用于回归任务。如果要预测单个值（例如，房屋的价格，给定其许多特征），则只需要单个输出神经元：其输出就是预测值。对于多元回归（即一次预测多个值），每个输出维度需要一个输出神经元。例如，要在图像中定位物体的中心，你需要预测2D坐标，因此需要两个输出神经元。如果还想在物体周围放置边框，则还需要两个数值：物体的宽度和高度。因此，得到了四个输出神经元。

Scikit-Learn包含一个MLPRegressor（多层感知机回归模型）类，用它来构建MLP，但是这个类不支持输出层中的激活函数。

MLPRegressor函数参数	参数的使用方法
hidden_layer_sizes	决定网络结构格式：tuple，（50,50,50）表示有三个隐藏层，每个隐藏层有50个神经元
activvation	激活函数 `'relu'`（默认）：整流线性单元，训练速度快，是目前最常用的。 `'tanh'`：双曲正切函数，输出以0为中心。 `'logistic'`：Sigmoid 函数，输出在0-1之间。
solver	权重优化的求解器 `'adam'`（默认）：适用于大多数情况，对大规模数据效果好。 `'lbfgs'`：适用于小数据集，收敛更精确更快，但耗内存。 `'sgd'`：随机梯度下降，可以配合动量（momentum）使用。
alpha	L2正则化系数，用于控制过拟合值越大，正则化强度越大，模型越简单
learning_rate_init	初始学习率如果solver 为adam或sgd，需要使用该参数。太大可能不收敛，太小则训练过慢
max_iter	最大迭代次数
early_stopping	是否使用早停

在房屋数据集上对其进行训练：为简单起见，我们将使用Scikit-Learn的fetch_california_housing()函数来加载数据。这个数据集只包含数值特征（没有ocean_proximity特征），并且没有缺失值。

下面的代码首先获取和拆分数据集，然后创建一个流水线来标准化输入特征，之后再将它们送到MLPRegressor。标准化神经网络非常重要，因为它们是使用梯度下降训练的，当特征具有非常不同的尺度时，梯度下降不会很好地收敛。最后，代码训练模型并评估其验证误差。

from sklearn.pipeline import make_pipeline
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScalerhousing = fetch_california_housing()  # 可能要换成作业5的数据集
X_train_full, X_test, y_train_full, y_test = train_test_split(housing.data, housing.target, random_state=42)
X_train, X_valid, y_train, y_valid = train_test_split(X_train_full, y_train_full, random_state=42)mlp_reg = MLPRegressor(hidden_layer_sizes=[50,50,50], random_state=42)
pipeline = make_pipeline(StandardScaler(), mlp_reg)
pipeline.fit(X_train, y_train)y_pred = pipeline.predict(X_valid)
rmse = mean_squared_error(y_valid, y_pred, squared=False)rmse

（3）MLP分类

二进制分类问题：只需要使用sigmoid激活函数的单个输出神经元：输出的是0和1之间的数字，可以将其解释为正类的估计概率，负类的估计概率 = 1-正类的估计概率。

多标签的二元分类任务：多个输出神经元，都使用激活函数。

多分类任务：每个类需要一个输出神经元，并且将输出层使用softmax激活函数，将确保所有估计的类概率都在0-1之间，并且它们加起来为1（因为分类是互斥的）。

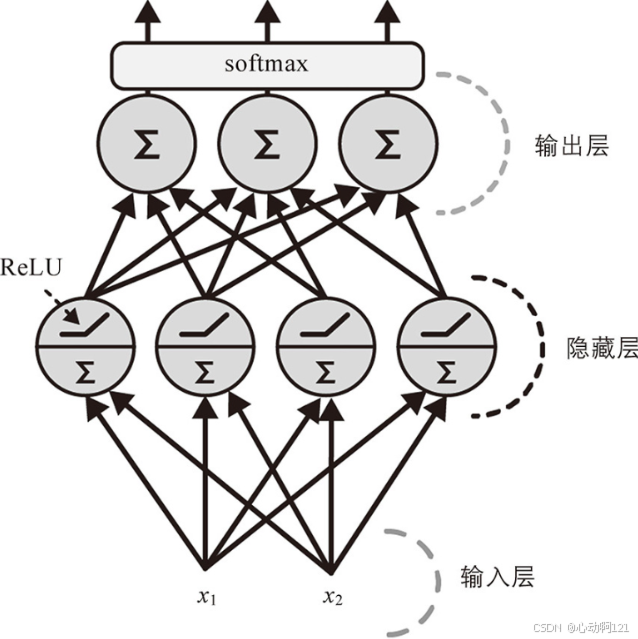
关于损失函数，由于正在预测概率分布，因此交叉熵损失（或对数损失）通常是一个不错的选择。 Scikit-Learn在`sklearn.neural_network`包中有一个`MLPClassifier`类。它几乎与`MLPRegressor`类相同，只是它最小化交叉熵而不是MSE。

超参数	二元分类	多标签二元分类	多分类
隐藏层	通常为1-5层，具体取决于任务
输出神经元数量	1个神经元	每个二元标签1个神经元	每个类1个神经元
输出层激活	sigmoid	sigmoid	sigmoid
损失函数	交叉熵	交叉熵	交叉熵