当前位置：首页 > backend >正文

机器学习之K-means（K-均值）算法

backend 2025/8/11 16:37:08

一、什么是 K-Means 聚类

K-Means 是一种经典的无监督学习算法，主要用于解决聚类问题。它的核心思想是将 n 个样本点划分为 k 个不同的簇，使得每个簇内的样本点具有较高的相似度，而不同簇之间的样本点差异较大。与监督学习不同，聚类不需要预先标记好的训练数据，算法会自动从数据中发现模式和结构，非常适合探索性数据分析。

二、聚类

什么是聚类？通俗说，聚类是将一堆数据划分成到不同的组中。

聚类（Clustering）的通俗定义：将一堆数据划分到不同的组中。一种无监督学习，其产生的类别是未知的。

聚类的学术定义：把一个数据对象的集合划分成簇（子集），使簇内对象彼此相似，簇间对象不相似的过程。

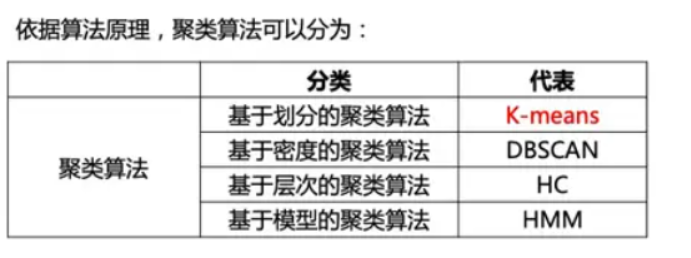
在聚类算法中，常用的是 K-means 和 DBSCAN，但本文聚焦 K-means 。

HMM即隐马尔可夫模型（HiddenMarkovModel）在语音识别、机器翻译、中文分词、命名实体识别、词性标注、基因识别等领域有广泛的使用。

三、K-Means 算法原理

K-Means 算法的工作流程可以概括为以下几个步骤：

距离度量通常使用欧氏距离，对于样本点 x 和质心 c，计算公式为：

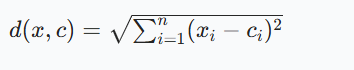
1.K-means如何确定 K 值？

K-means 常常根据 SSE 和轮廓系数确定 K 值。

初始化：随机选择 k 个样本点作为初始质心（聚类中心）
分配样本：计算每个样本点到各个质心的距离，将样本点分配到距离最近的质心所在的簇
更新质心：计算每个簇中所有样本点的均值，将其作为新的质心
迭代优化：重复步骤 2 和步骤 3，直到质心的位置变化小于预设阈值或达到最大迭代次数
收敛：当质心不再明显变化时，算法收敛，得到最终的聚类结果

方法一：尝试不同k值：多选取几个k值，对比聚类效果，选择最优的k值。

方法二：结合业务特点：假定想要把文章分为兵乒球，篮球，综合三个类型，就设定k=3。

方法三：根据SSE和轮廓系数：SSE越小，聚类效果越好；轮廓系数越大，聚类效果越好。

2. K-means如何选取初始中心点？

K-means选择不同的初始中心，会得到不同的聚类结果。

K-means 常使用 K-means++ 方法确定初始中心点。

K-means++：选择初始的聚类中心之间的相互距离要尽可能的远。

二分K-means：选择误差最大的类，进行二分分裂。

3. K-means如何处理空簇？

聚类中心没有被分配到样本，常常将其删除。

空簇问题：K-means中计划聚成20类，结果才聚成19类，1类为空。

空簇原因：聚类中心没有被分配到样本。

解决办法：

法一：其他簇心的均值点
法二：删除空族
法三：最远离聚类中心的点

4. K- means特征工程

类别特征、大数值特征都不适用于 K-means 聚类。

原因：K-means是基于距离的，而类别没有距离。

k-means对异常值明显，比如年龄、金额等。

5.K- means评估

什么样的 K-means 聚类才是好的 K-means 聚类？

实际应用中，常常把 SSE（Sum of Squared Errors，误差平方和）与轮廓系数（Silhouette Coefficient）结合使用，评估聚类模型的效果。

SSE：误差平方和（Sum of Squared Errors）最小，聚类效果最好。

轮廓系数（Silhouette Coefficient）：轮廓系数越大，聚类效果越好。

6. SSE

SSE越小，聚类效果越好。

7.轮廓系数

轮廓系数越大，聚类效果越好。

四、K-Means 的优缺点分析

优点：

算法简单易懂，实现方便
计算效率高，适合处理大规模数据集
聚类结果可解释性强

缺点：

需要预先指定 K 值，对结果影响较大
对初始质心的选择敏感，可能陷入局部最优
对噪声和异常值敏感
不适合发现非凸形状的簇

五、项目案列

基于 K-Means 聚类的啤酒数据分析与最佳聚类数探索

在数据分析领域，聚类分析是一种重要的无监督学习方法，可用于发现数据中的自然分组结构。本项目以啤酒相关数据（包含热量、钠含量、酒精含量、成本等属性）为研究对象，利用 K-Means 聚类算法对其进行分析，通过轮廓系数确定最佳聚类数，挖掘不同啤酒在这些属性上的聚类特征，为啤酒市场细分、产品研发等提供数据参考。

实现步骤:

（一）数据读取与预处理

数据读取：
使用 pandas 的 read_csv 函数读取啤酒数据文件 data.txt，由于数据是以空格分隔，设置 sep=' ' ，并指定编码为 utf-8 ，确保正确读取数据内容，代码如下：

beer = pd.read_csv('data.txt', sep=' ', encoding='utf-8')

特征提取：

提取除啤酒名称外的其他列作为特征数据 x，这些特征将用于后续聚类分析，代码为：

x = beer.iloc[:, 1:]

（二）确定最佳聚类数（K 值）

轮廓系数介绍：
轮廓系数（Silhouette Score）是评估聚类效果的常用指标，其取值范围在 [-1, 1] 之间。值越接近 1，表示聚类效果越好，即类内样本相似度高，类间样本差异大；值越接近 -1，则聚类效果越差。
遍历不同 K 值计算轮廓系数：
定义要尝试的聚类数列表 k = [2, 3, 4, 5, 6]，通过遍历该列表，对每个 k 值，使用 KMeans 算法进行聚类，并计算对应的轮廓系数。为避免算法因初始化中心不同导致结果波动，设置 n_init=10 （指定算法运行次数，取最优结果），代码如下：

scores = []
k_list = [2, 3, 4, 5, 6]
for i in k_list:model = KMeans(n_clusters=i, n_init=10)  model.fit(x)labels = model.labels_score = metrics.silhouette_score(x, labels)scores.append(score)

3.确定最佳 K 值：

通过 numpy 的 argmax 函数找到轮廓系数最大值对应的索引，进而从 k_list 中确定最佳聚类数 best_k，代码为：

best_k = k_list[np.argmax(scores)]
print("最佳K值：", best_k)

（三）最佳 K 值聚类及效果评估

最佳 K 值聚类：使用确定的最佳 K 值，再次构建 KMeans 模型进行聚类，得到最终的聚类标签 labels，代码如下：

model = KMeans(n_clusters=best_k, n_init=10)
model.fit(x)
labels = model.labels_

2.聚类效果评估：
计算并输出最佳 K 值下聚类结果的轮廓系数，评估聚类效果，代码为：

print('轮廓系数：', metrics.silhouette_score(x, labels))

（四）聚类结果可视化

可基于 matplotlib 绘制散点图等，将不同聚类的啤酒数据在特征空间中展示出来。例如，选取两个特征维度（如热量和钠含量），以聚类标签区分颜色绘制散点图，代码示例（需根据实际特征调整）：

plt.scatter(x.iloc[:, 0], x.iloc[:, 1], c=labels)
plt.xlabel(beer.columns[1])
plt.ylabel(beer.columns[2])
plt.title(f'K-Means Clustering Result with Best K={best_k}')
plt.show()

完整代码及运行结果如下：

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn import metrics
from sklearn.cluster import KMeans# 根据实际情况修改分隔符，比如空格分隔就用sep=' '，逗号分隔用sep=','
beer = pd.read_csv('data.txt', sep=' ', encoding='utf-8')  # 这里修改了sep参数
x = beer.iloc[:, 1:]
scores = []
k = [2, 3, 4, 5, 6]for i in k:model = KMeans(n_clusters=i, n_init=10)  # 增加了n_init参数，避免警告model.fit(x)labels = model.labels_score = metrics.silhouette_score(x, labels)scores.append(score)best_k = k[np.argmax(scores)]
print("最佳K值：", best_k)model = KMeans(n_clusters=best_k, n_init=10)
model.fit(x)
labels = model.labels_
print('轮廓系数：', metrics.silhouette_score(x, labels))
plt.scatter(x.iloc[:, 0], x.iloc[:, 1], c=labels)
plt.xlabel(beer.columns[1])
plt.ylabel(beer.columns[2])
plt.title(f'K-Means Clustering Result with Best K={best_k}')
plt.show()

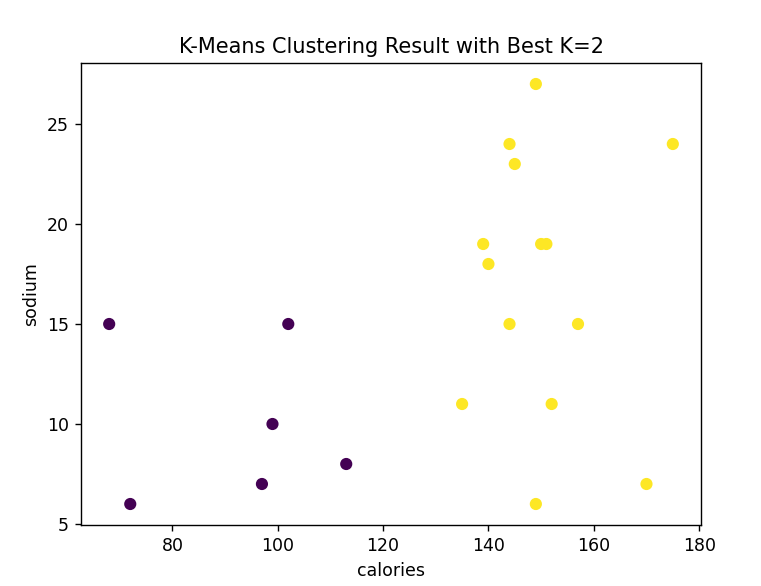本项目通过 Python 结合 pandas、numpy、matplotlib、sklearn 等库，实现了对啤酒数据的 K-Means 聚类分析。利用轮廓系数确定最佳聚类数，有效评估聚类效果，挖掘出啤酒数据在多属性下的聚类特征。后续可进一步拓展，如结合更多元的啤酒数据（市场销量、用户评价等）深化分析，或尝试其他聚类算法（如层次聚类）进行对比，丰富项目成果，为啤酒行业相关决策提供更全面的数据支撑。