快速傅里叶变换FFT推导以及运算复杂度分析
对于长度为 NNN 的序列 x[n]x[n]x[n] ,DFT公式如下
X[k]=∑n=0N−1x[n]WNkn,0⩽k⩽N−1x[n]=1N∑k=0N−1X[k]WN−nk,0⩽n⩽N−1
X[k]=\sum_{n=0}^{N-1} x[n] W_N^{k n}, \quad 0 \leqslant k \leqslant N-1 \\
x[n]=\frac{1}{N} \sum_{k=0}^{N-1} X[k] W_N^{-n k}, \quad 0 \leqslant n \leqslant N-1
X[k]=n=0∑N−1x[n]WNkn,0⩽k⩽N−1x[n]=N1k=0∑N−1X[k]WN−nk,0⩽n⩽N−1
其中
WN=e−j2π/N
W_N=\mathrm{e}^{-\mathrm{j} 2 \pi / N}
WN=e−j2π/N
相位因子 WNW_NWN 具有对称性和周期性
WNk+N/2=−WNkWNk+N=WNk
W_N^{k+N / 2}=-W_N^k \\
W_N^{k+N}=W_N^k
WNk+N/2=−WNkWNk+N=WNk
将 X[k]X[k]X[k] 和 x[n]x[n]x[n] 写成复数形式,则
XR[k]+jXI[k]=∑n=0N−1(xR[n]+jxI[n])(cos2πknN−jsin2πknN)
X_R[k]+\mathrm{j}X_I[k]=\sum_{n=0}^{N-1}(x_R[n]+\mathrm{j}x_I[n])(\cos \frac{2 \pi k n}{N}-\mathrm{j}\sin \frac{2 \pi k n}{N})
XR[k]+jXI[k]=n=0∑N−1(xR[n]+jxI[n])(cosN2πkn−jsinN2πkn)
显然
XR[k]=∑n=0N−1(xR[n]cos2πknN+xI[n]sin2πknN)XI[k]=−∑n=0N−1(xR[n]sin2πknN−xI[n]cos2πknN)
\begin{aligned}
& X_R[k]=\sum_{n=0}^{N-1}(x_R[n] \cos \frac{2 \pi k n}{N}+x_I[n] \sin \frac{2 \pi k n}{N}) \\
& X_I[k]=-\sum_{n=0}^{N-1}(x_R[n] \sin \frac{2 \pi k n}{N}-x_I[n] \cos \frac{2 \pi k n}{N})
\end{aligned}
XR[k]=n=0∑N−1(xR[n]cosN2πkn+xI[n]sinN2πkn)XI[k]=−n=0∑N−1(xR[n]sinN2πkn−xI[n]cosN2πkn)
对于一个 NNN 点复序列,直接求解 DFT 需要的计算次数为:
(1)计算一个 X[k]X[k]X[k] 需要 2N2N2N 次三角函数计算,因此计算所有 NNN 项 X[k]X[k]X[k] 需要 2N22N^22N2 次三角函数计算;
(2)计算一个 X[k]X[k]X[k] 需要 4N4N4N 次实数乘法,因此计算所有 NNN 项 X[k]X[k]X[k] 需要 4N24N^24N2 次实数乘法;
(3) XR[k]X_R[k]XR[k] 求和每一项需要 111 次实数加法,总共有 NNN 项,求和时项与项之间需要 N−1N-1N−1 次实数加法,因此计算一个 XR[k]X_R[k]XR[k] 需要 2N−12N-12N−1 次实数加法。同理 XI[k]X_I[k]XI[k] 也需要 2N−12N-12N−1 次实数加法。 因此计算所有 NNN 项 X[k]X[k]X[k] 需要 N(4N−2)N(4N-2)N(4N−2) 次实数加法。
假设 NNN 为 222 的指数幂,即 N=2pN=2^pN=2p 。先看 N=8N=8N=8 的情况
X[k]=x[0]+x[1]W8k+x[2]W82k+x[3]W83k+x[4]W84k+x[5]W8k+x[6]W86k+x[7]W87k=x[0]+x[2]W82k+x[4]W84k+x[6]W86k+(x[1]W8k+x[3]W83k+x[5]W85k+x[7]W87k)=x[0]+x[2]W4k+x[4]W42k+x[6]W43k+W8k(x[1]+x[3]W4k+x[5]W42k+x[7]W43k)
\begin{aligned}
X[k]&=x[0]+x[1]W_8^{k}+x[2]W_8^{2k}+x[3]W_8^{3k}+x[4]W_8^{4k}+x[5]W_8^{k}+x[6]W_8^{6k}+x[7]W_8^{7k} \\
&=x[0]+x[2]W_8^{2k}+x[4]W_8^{4k}+x[6]W_8^{6k}+(x[1]W_8^{k}+x[3]W_8^{3k}+x[5]W_8^{5k}+x[7]W_8^{7k}) \\
&=x[0]+x[2]W_4^{k}+x[4]W_4^{2k}+x[6]W_4^{3k}+W_8^{k}(x[1]+x[3]W_4^{k}+x[5]W_4^{2k}+x[7]W_4^{3k})
\end{aligned}
X[k]=x[0]+x[1]W8k+x[2]W82k+x[3]W83k+x[4]W84k+x[5]W8k+x[6]W86k+x[7]W87k=x[0]+x[2]W82k+x[4]W84k+x[6]W86k+(x[1]W8k+x[3]W83k+x[5]W85k+x[7]W87k)=x[0]+x[2]W4k+x[4]W42k+x[6]W43k+W8k(x[1]+x[3]W4k+x[5]W42k+x[7]W43k)
定义序列 y[n]=x[2n]y[n]=x[2n]y[n]=x[2n] ,即 y[0]=x[0]y[0]=x[0]y[0]=x[0] , y[1]=x[2]y[1]=x[2]y[1]=x[2] , y[2]=x[4]y[2]=x[4]y[2]=x[4] , y[3]=x[6]y[3]=x[6]y[3]=x[6] 。
定义序列 z[n]=x[2n+1]z[n]=x[2n+1]z[n]=x[2n+1] ,即 z[0]=x[1]z[0]=x[1]z[0]=x[1] , z[1]=x[3]z[1]=x[3]z[1]=x[3] , z[2]=x[5]z[2]=x[5]z[2]=x[5] , z[3]=x[7]z[3]=x[7]z[3]=x[7] 。
则当 0≤k≤30\le k\le 30≤k≤3 时
Y[k]=y[0]+y[1]W4k+y[2]W42k+y[3]W43k=x[0]+x[2]W4k+x[4]W42k+x[6]W43kZ[k]=z[0]+z[1]W4k+z[2]W42k+z[3]W43k=x[1]+x[3]W4k+x[5]W42k+x[7]W43k
Y[k]=y[0]+y[1]W_4^{k}+y[2]W_4^{2k}+y[3]W_4^{3k}=x[0]+x[2]W_4^{k}+x[4]W_4^{2k}+x[6]W_4^{3k} \\
Z[k]=z[0]+z[1]W_4^{k}+z[2]W_4^{2k}+z[3]W_4^{3k}=x[1]+x[3]W_4^{k}+x[5]W_4^{2k}+x[7]W_4^{3k}
Y[k]=y[0]+y[1]W4k+y[2]W42k+y[3]W43k=x[0]+x[2]W4k+x[4]W42k+x[6]W43kZ[k]=z[0]+z[1]W4k+z[2]W42k+z[3]W43k=x[1]+x[3]W4k+x[5]W42k+x[7]W43k
因此有
X[k]=Y[k]+W8kZ[k]
X[k]=Y[k]+W_8^{k}Z[k]
X[k]=Y[k]+W8kZ[k]
当 4≤k≤74\le k\le 74≤k≤7 时,令 m=k−4m=k-4m=k−4 ,则
X[k]=x[0]+x[2]W4k+x[4]W42k+x[6]W43k+W8k(x[1]+x[3]W4k+x[5]W42k+x[7]W43k)=x[0]+x[2]W4m+4+x[4]W42(m+4)+x[6]W43(m+4)+W8m+4(x[1]+x[3]W4m+4+x[5]W42(m+4)+x[7]W43(m+4))=x[0]+x[2]W4m+x[4]W42m+x[6]W43m−W8m(x[1]+x[3]W4m+x[5]W42m+x[7]W43m)
\begin{aligned}
X[k]&=x[0]+x[2]W_4^{k}+x[4]W_4^{2k}+x[6]W_4^{3k}+W_8^{k}(x[1]+x[3]W_4^{k}+x[5]W_4^{2k}+x[7]W_4^{3k}) \\
&=x[0]+x[2]W_4^{m+4}+x[4]W_4^{2(m+4)}+x[6]W_4^{3(m+4)}+W_8^{m+4}(x[1]+x[3]W_4^{m+4}+x[5]W_4^{2(m+4)}+x[7]W_4^{3(m+4)}) \\
&=x[0]+x[2]W_4^{m}+x[4]W_4^{2m}+x[6]W_4^{3m}-W_8^{m}(x[1]+x[3]W_4^{m}+x[5]W_4^{2m}+x[7]W_4^{3m})
\end{aligned}
X[k]=x[0]+x[2]W4k+x[4]W42k+x[6]W43k+W8k(x[1]+x[3]W4k+x[5]W42k+x[7]W43k)=x[0]+x[2]W4m+4+x[4]W42(m+4)+x[6]W43(m+4)+W8m+4(x[1]+x[3]W4m+4+x[5]W42(m+4)+x[7]W43(m+4))=x[0]+x[2]W4m+x[4]W42m+x[6]W43m−W8m(x[1]+x[3]W4m+x[5]W42m+x[7]W43m)
因此有
X[k]=Y[k−4]−W8k−4Z[k−4]
X[k]=Y[k-4]-W_8^{k-4}Z[k-4]
X[k]=Y[k−4]−W8k−4Z[k−4]
综上
X[k]={Y[k]+W8kZ[k]0≤k≤3Y[k−4]−W8k−4Z[k−4]4≤k≤7
X[k]=
\left\{\begin{array}{l}Y[k]+W_8^{k}Z[k] & \quad 0\le k\le 3 \\Y[k-4]-W_8^{k-4}Z[k-4] & \quad 4\le k\le 7\end{array}
\right.
X[k]={Y[k]+W8kZ[k]Y[k−4]−W8k−4Z[k−4]0≤k≤34≤k≤7
蝶形图如下
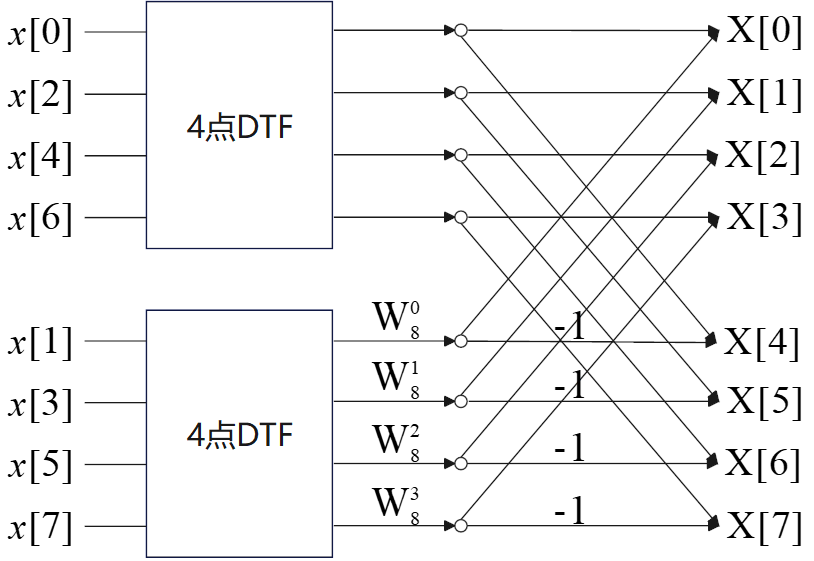
继续求 y[n]y[n]y[n] 和 z[n]z[n]z[n] 的 DFT 。
以 y[n]y[n]y[n] 为例,令 a[n]=y[2n]a[n]=y[2n]a[n]=y[2n] ,即 a[0]=y[0]=x[0]a[0]=y[0]=x[0]a[0]=y[0]=x[0] , a[1]=y[2]=x[4]a[1]=y[2]=x[4]a[1]=y[2]=x[4] 。
令 b[n]=y[2n+1]b[n]=y[2n+1]b[n]=y[2n+1] , 即 b[0]=y[1]=x[2]b[0]=y[1]=x[2]b[0]=y[1]=x[2] , b[1]=y[3]=x[6]b[1]=y[3]=x[6]b[1]=y[3]=x[6] 。
同理得到
y[k]={A[k]+W4kB[k]0≤k≤1A[k−2]−W4kB[k−2]2≤k≤3
y[k]=
\left\{\begin{array}{l}A[k]+W_4^{k}B[k] & \quad 0\le k\le 1 \\A[k-2]-W_4^{k}B[k-2] & \quad 2\le k\le 3\end{array}
\right.
y[k]={A[k]+W4kB[k]A[k−2]−W4kB[k−2]0≤k≤12≤k≤3
z[n]z[n]z[n] 的 4点 DFT 计算方法相同。
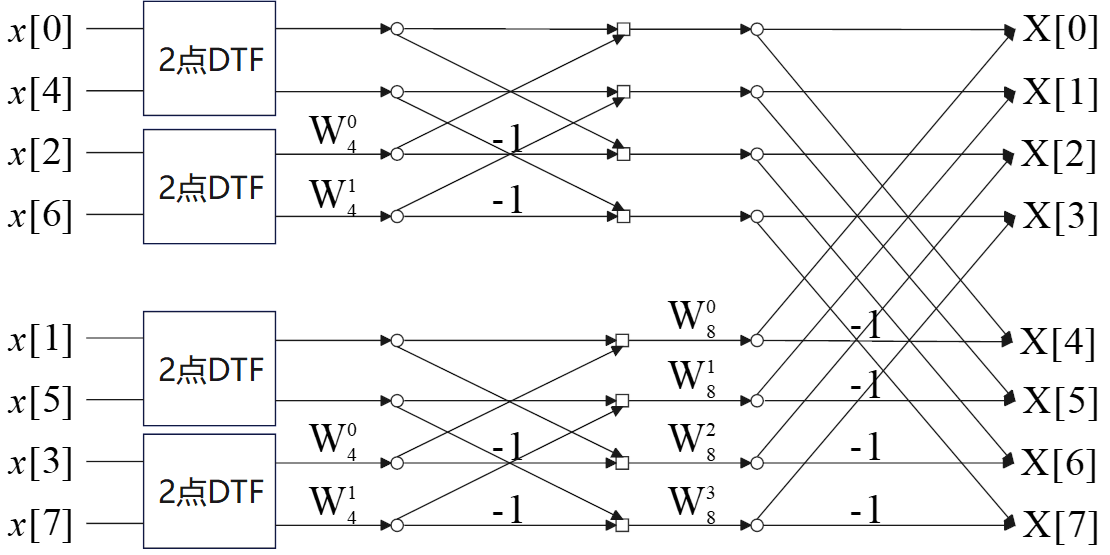
最后以 a[n]a[n]a[n] 为例
A[k]=a[0]+a[1]W2k=x[0]+x[4]W2k
A[k]=a[0]+a[1]W_{2}^{k}=x[0]+x[4]W_{2}^{k}
A[k]=a[0]+a[1]W2k=x[0]+x[4]W2k
即
A[0]=x[0]+W20x[4]=x[0]+x[4]A[1]=x[0]−W20x[4]=x[0]−x[4]
A[0]=x[0]+W_2^0x[4]=x[0]+x[4] \\
A[1]=x[0]-W_2^0x[4]=x[0]-x[4]
A[0]=x[0]+W20x[4]=x[0]+x[4]A[1]=x[0]−W20x[4]=x[0]−x[4]
2点 DFT 的算法相同。
完整蝶形图
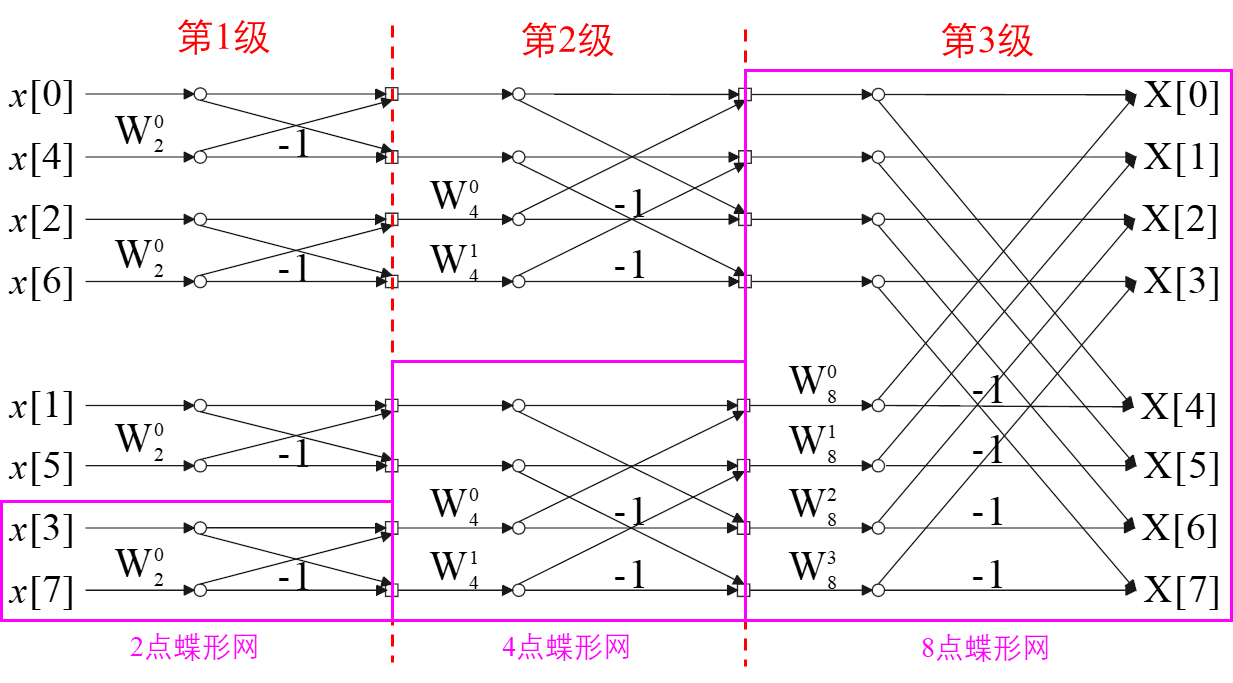
对于一个 NNN 点复序列,假设 N=2mN=2^mN=2m ,使用 FFT 的计算次数为:
(1)只需要计算 WN0,WN1,...,WNN/2−1W_N^0, W_N^1, ..., W_N^{N/2-1}WN0,WN1,...,WNN/2−1 这 N/2N/2N/2 个不同的旋转因子。而每个旋转因子对应2次三角函数运算,因此总共需要 NNN 次三角函数计算。注意,如图8点 FFT 示例中由于 W20=W40=W80W_2^0=W_4^0=W_8^0W20=W40=W80 以及 W41=W82W_4^1=W_8^2W41=W82 ,因此看作相同运算。
(2)FFT 由 mmm 级构成。研究第 ppp 级,则该级有 2m−p2^{m-p}2m−p 个 2p2^p2p 个节点的蝶形网(蝶形网定义如图)。对于 s=2ps=2^ps=2p 个节点的蝶形网,有公式
X[k]={Y[k]+WskZ[k]0≤k≤s/2−1Y[k−4]−Wsk−4Z[k−4]s/2≤k≤s−1
X[k]=
\left\{\begin{array}{l}Y[k]+W_s^{k}Z[k] & \quad 0\le k\le s/2-1 \\Y[k-4]-W_s^{k-4}Z[k-4] & \quad s/2\le k\le s-1\end{array}
\right.
X[k]={Y[k]+WskZ[k]Y[k−4]−Wsk−4Z[k−4]0≤k≤s/2−1s/2≤k≤s−1
其中 Y[k]Y[k]Y[k] 和 Z[k]Z[k]Z[k] 是输入节点, X[k]X[k]X[k] 是输出节点。
由
WpkZ[k]=(Re{Wsk}+jIm{Wsk})(Re{Z[k]}+jIm{Z[k]})=(Re{Wsk}Re{Z[k]}−Im{Wsk}Im{Z[k])+j(Re{Wsk}Im{Z[k]}+Im{Wsk}Re{Z[k]})
\begin{aligned}
W_p^kZ[k]&=(Re\{W_s^k\}+\mathrm{j}Im\{W_s^k\})(Re\{Z[k]\}+\mathrm{j}Im\{Z[k]\}) \\
&=(Re\{W_s^k\}Re\{Z[k]\}-Im\{W_s^k\}Im\{Z[k])+\mathrm{j}(Re\{W_s^k\}Im\{Z[k]\}+Im\{W_s^k\}Re\{Z[k]\})
\end{aligned}
WpkZ[k]=(Re{Wsk}+jIm{Wsk})(Re{Z[k]}+jIm{Z[k]})=(Re{Wsk}Re{Z[k]}−Im{Wsk}Im{Z[k])+j(Re{Wsk}Im{Z[k]}+Im{Wsk}Re{Z[k]})
可见运算 WskZ[k]W_s^kZ[k]WskZ[k] 需要4次乘法和2次实数加法。注意后面两项 WskZ[k]W_s^{k}Z[k]WskZ[k] 和 Wsk−4Z[k−4]W_s^{k-4}Z[k-4]Wsk−4Z[k−4] 是相等的,因此每个蝶形网内对于 WskZ[k]W_s^{k}Z[k]WskZ[k] 和 Wsk−4Z[k−4]W_s^{k-4}Z[k-4]Wsk−4Z[k−4] 项需要计算 s/2×4s/2\times4s/2×4 次乘法以及 s/2×2s/2\times 2s/2×2 次加法。
总乘法计算量为 m×2m−p×s/2×4=2Nlog2Nm\times2^{m-p}\times s/2\times4=2N\log_2 Nm×2m−p×s/2×4=2Nlog2N 。
(3)对于 Y[k]+WpkZ[k]Y[k]+W_p^{k}Z[k]Y[k]+WpkZ[k] 和 Y[k−4]−Wpk−4Z[k−4]Y[k-4]-W_p^{k-4}Z[k-4]Y[k−4]−Wpk−4Z[k−4] ,两个复数相加需要2次加法,因此总实数加法数为 m×2m−p×[(s/2×2)+s×2]=3Nlog2Nm\times2^{m-p}\times[(s/2\times2)+s\times2]=3N\log_2 Nm×2m−p×[(s/2×2)+s×2]=3Nlog2N 。
总结
| 计算类别 | 直接计算DFT | 采用FFT |
|---|---|---|
| 三角函数计算 | 2N22N^22N2 | NNN |
| 实数乘法 | 4N24N^24N2 | 2Nlog2N2N \log_2 N2Nlog2N |
| 实数加法 | N(4N−2)=4N2−2NN(4N-2) = 4N^2 - 2NN(4N−2)=4N2−2N | 3Nlog2N3N\log_2 N3Nlog2N |
