当前位置：首页 > ai >正文

【CF】Day136——Codeforces Round 1046 (Div. 2) CD (动态规划 | 数学)

ai 2025/9/1 19:57:09

C. Against the Difference

题目：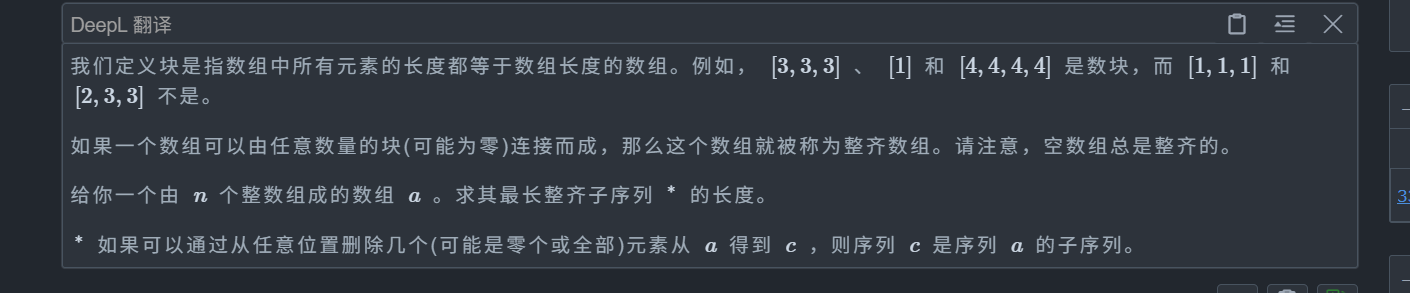

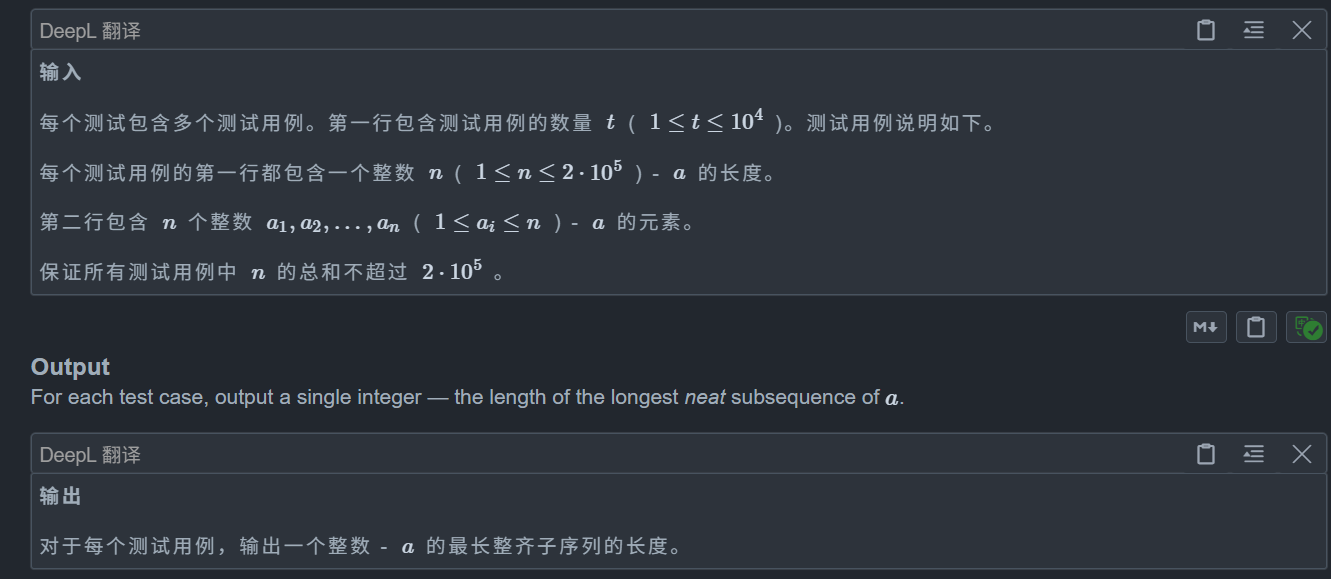思路：

简单DP

不难发现我们贪心是没法贪的，因此考虑DP

我们令 dp[i] 为前 i 个元素能构造出的最长整齐子序列的长度，不难发现一个很简单的转移，即直接继承 dp[i] = dp[i-1]，那么现在考虑增加奉献的情况

对于 a[i]，如果我们此时要选择增加奉献，那么就要从前 a[i] 个位置转移，且这 a[i] 个位置 j 的 a[j] 都是 a[i]

所以考虑储存 a[i] 的位置，如果 pos[a[i]].size() >= a[i]，那么说明此时可以转移，贪心的想，我们肯定是越后转移越好，所以我们直接从前 a[i] 个位置转移即可，此时增加的奉献就是 a[i]

具体实现看代码

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());void solve()
{int n, x;cin >> n;vector<int> dp(n + 1, 0);vector<vector<int>> pos(n + 1);for (int i = 1; i <= n; i++){cin >> x;dp[i] = dp[i - 1];pos[x].push_back(i);if (pos[x].size() >= x)dp[i] = max(dp[i], dp[pos[x][pos[x].size() - x] - 1] + x);}cout << dp[n] << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

D. For the Champion

题目：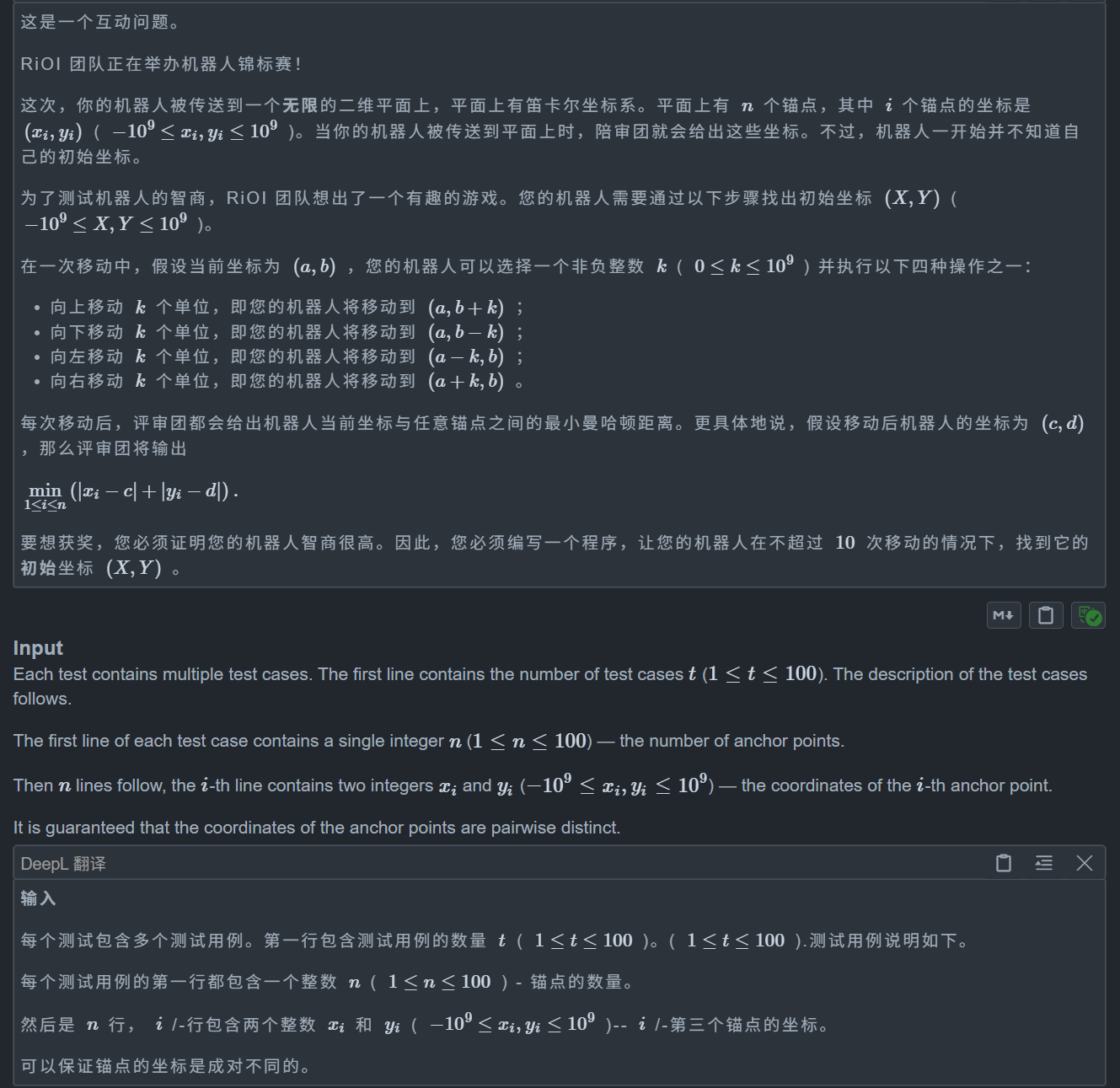

思路：

经典距离

我们不难发现，绝对值很麻烦，所以我们应该考虑删除绝对值的影响

同时我们还能发现，如果 k 很小，这其实不利于我们寻找，因为会有很多的节点干扰我们

所以我们考虑一个很大的坐标，如 (∞，∞)，这样的话我们肯定能确定是哪个点的结果

考虑十步内得出，我们不妨考虑两个极端： P1 (∞，∞)，P2 (∞，-∞)

我们假设求出的答案是 ask，原始坐标是 (x, y)

①.对于 P1，我们不难写出对应式子

$\left | x+x_m-x_i \right |+\left | y+y_m-y_i \right |=ask$

其中 x/y_m 代表移动的距离，x/y_i 代表距离最短时对应的点，那么拆开就有（这里直接化简）

$x+y=ask-x_m-y_m+x_i+y_i$

其中两个 x/y_m 都是 ∞ 均为已知量，那么为了让 ask 最小，我们的 x_i + y_i 肯定是最大的，所以预处理即可

②.对于 P2，我们同理可写出

$\left | x+x_m-x_i \right |+\left | y-y_m-y_i \right |=ask$

但是由于此时 y-y_m 小于 y_i，因此考虑变号，则有

$x+x_m-x_i+(y_i - y + y_m) = ask$

化简得

$x-y=ask-x_m-y_m-(y_i - x_i)$

同理为了让 ask 最小，我们就要让 y_i - x_i 最小，所以也是预处理出来

我们将上面两个式子优化一下，则有

$x+y=res1$

$x-y=res2$

由于 res1 和 res2 我们可以求出来，那么也就能求出 x,y 的坐标

具体的，由于我们无法一次直接移动 ∞ 长度，那我们就移动一个很长的距离即可，由于 k <= 1e9，所以我们考虑移动四次 1e9，其中两次 R 来达到 x 轴无限远，两次 D 来达到 y 轴无限远，这样就能得到一个 res 了

而对于另一个 res，我们直接四次 U 即可，因为 x 轴无限远了，所以只需要考虑 y 轴，所以先两次抵消向下无限远，然后向上即可，这样另一个 res 也解决了

综上，我们只使用了 8 次即可完成问题

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());void solve()
{int n;cin >> n;int mx = -1e18, mi = 1e18;for (int i = 0; i < n; i++){int x, y;cin >> x >> y;mi = min(mi, y - x);mx = max(mx, x + y);}int ask;cout << "? R 1000000000" << endl;cin >> ask;cout << "? R 1000000000" << endl;cin >> ask;cout << "? D 1000000000" << endl;cin >> ask;cout << "? D 1000000000" << endl;cin >> ask;int res1 = ask - 4000000000LL - mi;cout << "? U 1000000000" << endl;cin >> ask;cout << "? U 1000000000" << endl;cin >> ask;cout << "? U 1000000000" << endl;cin >> ask;cout << "? U 1000000000" << endl;cin >> ask;int res2 = ask - 4000000000LL + mx;cout << "! " << (res1 + res2) / 2 << " " << (res2 - res1) /2 << endl;
}signed main()
{int t = 1;cin >> t;while (t--){solve();}return 0;
}

查看全文

http://www.xdnf.cn/news/19243.html