有限字长效应

数字信号处理的实质为数值运算。运算过程中，系统中的系数、输入输出等都要以二进制的形式存储在有限长的存储单元中，此时有限长度的数的精度就是有限的。具体实现中可能会产生误差。在数字系统中因有限字长引起误差的因素主要为以下三种：

1. AD 转换器把模拟输入信号转换成一组离散电平时产生的量化效应。
2. 把系数用有限位的二进制数表示时产生的量化效应。
3. 在运算过程中，为限制字长而进行的截断操作和防止溢出而压缩信号电平的有限字长效应。

1 AD 转换的有限字长效应

AD 转换器可分为两部分：采样和量化。采样将连续的模拟信号转为离散信号，量化将每个采样值用有限字长表示。其统计意义上的等价结构如图所示：

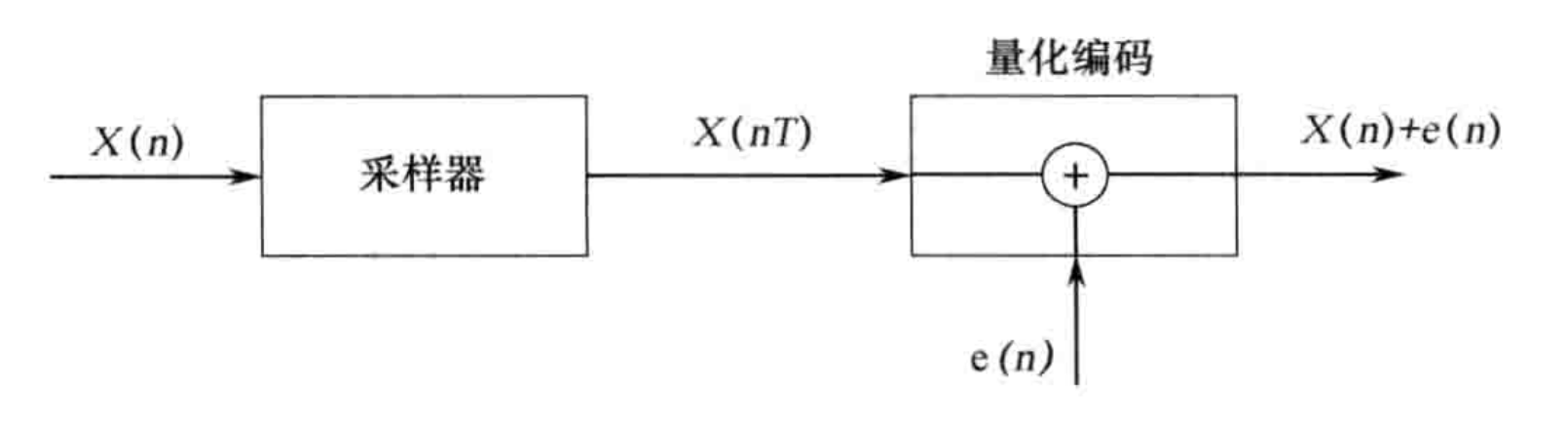
量化后的取值可以表示为精确取样值和量化误差的和，即
$$\hat{x}(n)=Q[x(n)]=x(n)+e(n)$$
这一模型基于以下假设：

• $e(n)$ 是一个平稳随机取样序列
• $e(n)$ 具有等概分布特性
• $e(n)$ 具有白噪声过程
• $e(n)$ 与 $x(n)$ 不相关
  由于 $e(n)$ 具有等概分布，舍入误差、补码截尾、原码截尾的概率分布如下所示：
  
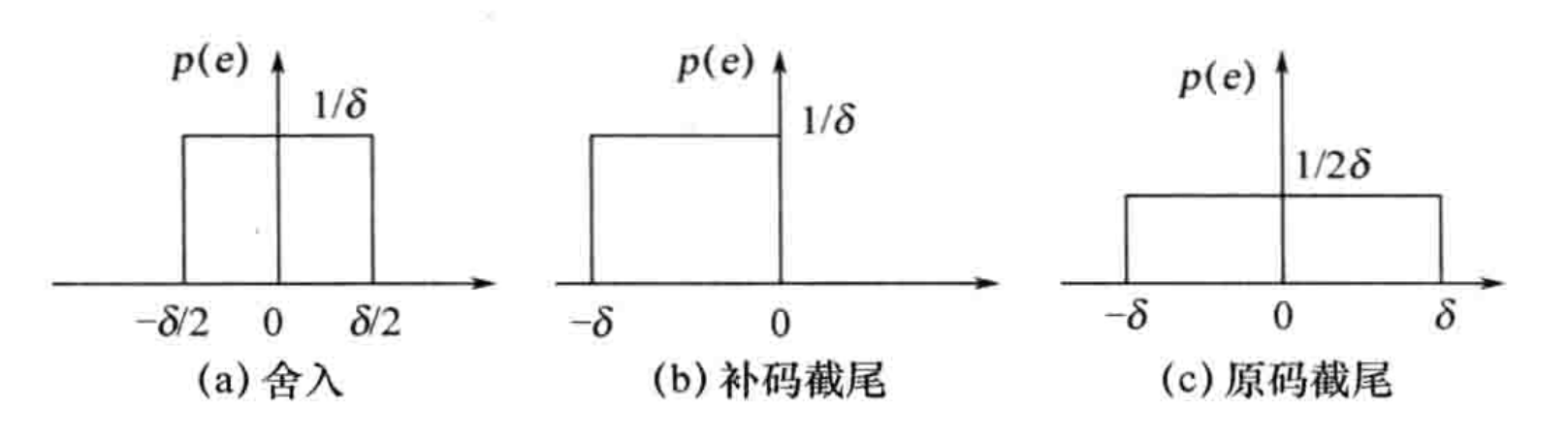
• 舍入时，均值为 0，方差为 $\frac{{\delta }^2}{2}$
• 补码截尾时，均值为 $-\frac{\delta }{2}$，方差为 $\frac{{\delta }^2}{12}$
• 原码截尾时，均值为 0，方差为 $\frac{{\delta }^2}{3}$
  量化信噪比的表达式为
  $$\begin{gathered} SN{R}_{AD}=10\lg (\frac{{\delta }_x^2}{{\delta }_e^2})=10\lg (12\times 2^{2L}{\delta }_x^2) \\ =6.02B+10.79+10\lg ({\delta }_x^2) \end{gathered}$$
  可得舍入后，字长每增加 1 位，SNR 约增加 6dB。

2 系统运算中的有限字长效应

对于二进制运算来讲，定点数的加法不会改变字长，但可能造成数据溢出。定点数的乘法存在字长效应，因为 2 个 B 位字长的定点数相乘，要保留所有有效位的话需要 2B 位字长的数据，数据截尾或舍入必然会引入字长效应。
如果在计算过程中增加字长来保证运算结果不产生截尾和舍入的话，耗费资源变多，在没有反馈的系统中可以如此操作。如果在有反馈网络的系统中，如数字滤波器，每次闭环运算都会增加一部分字长，循环运算下来需要的资源越来越多。