深度学习-----详解MNIST手写数字数据集的神经网络实现过程
数据集准备
使用
minis模块自动下载手写数字数据集(MNIST),包含训练集(6万张)和测试集(1万张),无需手动切分。数据已预分为训练集和测试集,直接读取即可。
神经网络结构设计
输入层:28×28图片展平为784个神经元。
隐藏层:
第一隐藏层:128个神经元(全连接层)。
第二隐藏层:256个神经元(全连接层)。
输出层:10个神经元(对应0-9分类)。
网络结构:输入→Flatten→全连接层→ReLU激活→全连接层→Softmax输出。
数据处理与设备分配
使用
DataLoader将数据打包为批次(batch size=64),提高GPU利用率。数据和模型需加载至同一设备(GPU/CPU),否则训练报错。
模型训练流程
前向传播:
输入数据经Flatten层展平后,依次通过全连接层和激活函数,最终输出预测概率。
损失函数:采用交叉熵损失函数(适用于多分类任务)。
反向传播:通过优化器(如SGD或Adam)计算梯度并更新权重参数。
训练策略:共训练10轮,每批次计算平均损失并优化。
关键细节与调试
权重参数初始化为随机值,训练过程中动态更新。
总参数量约14万(输入层展平参数+隐藏层权重)。
调试时需确保数据与模型在同一设备,避免因设备不匹配导致运行失败
网络结构:输入→Flatten→全连接层→ReLU激活→全连接层→Softmax输出
这个网络结构是一个典型的多层感知机(MLP),常用于处理分类任务(如手写数字识别、图像分类等)。以下是各层的作用和整体流程的详细解析:
1. 输入层 → Flatten
功能:将多维输入数据(如图像的像素矩阵)展平为一维向量。
举例:若输入是28×28的灰度图像,Flatten后会变成长度为784(28×28)的一维向量。
必要性:全连接层(Dense层)只能处理标量输入,需通过Flatten将多维数据转换为线性形式。
2. Flatten → 全连接层(第一层)

3. ReLU激活函数

4. 全连接层(第二层)

5. Softmax输出层

整体流程总结
输入预处理:图像被展平为向量。
特征提取:通过两层全连接层逐步提取从低级到高级的特征。
非线性建模:ReLU激活确保模型能拟合复杂函数。
概率预测:Softmax输出最终分类结果。
适用场景
图像分类(如MNIST手写数字识别)。
简单回归/分类问题(需根据任务调整最后一层的激活函数,如二分类用Sigmoid)。
作为复杂模型的基础模块(可堆叠CNN、RNN等其他层)。
关键参数调整
全连接层神经元数量:需平衡模型复杂度(如128→256)。
激活函数选择:ReLU适合大多数情况,但对某些任务可能需要Leaky ReLU或PReLU。
学习率与正则化:防止过拟合(如Dropout、L2正则化)。
使用DataLoader将数据打包为批次(batch size=64),提高GPU利用率
使用 DataLoader 将数据打包为批次(batch size=64)是深度学习中提升 GPU 利用率的关键步骤之一。以下是详细的解释:
1. DataLoader 的核心作用
DataLoader 是 PyTorch 提供的工具,用于将数据集分批次加载到内存中,并支持多线程数据加载、打乱数据顺序等功能。其核心作用包括:
数据分批:将大量数据划分为小批次(如每批 64 个样本),避免一次性加载所有数据占用过多内存。
并行加载:通过
num_workers参数启用多线程,加速数据读取(尤其在磁盘 I/O 密集型任务中)。自动迭代:简化训练循环,通过
for batch in DataLoader逐批获取数据。
2. 为什么需要分批次?
GPU 并行计算:现代 GPU 擅长并行处理大量数据。若单次仅处理 1 个样本,GPU 的计算单元无法充分利用,且频繁的内存读写会显著降低效率。
梯度计算优化:损失函数和反向传播通常基于批次数据计算(如均方误差、交叉熵),分批次可避免单样本梯度噪声过大。
显存管理:大批次可减少迭代次数,但需权衡显存容量(例如,若单张图片为 784 维向量,64 张图片占显存约 64×784≈500KB,而单张则仅需 784B)。
3. 具体实现流程
(1) 数据预处理与打包
假设输入为 MNIST 手写数字图像(28×28 像素):
from torchvision import datasets, transforms
from torch.utils.data import DataLoader# 定义数据转换(如归一化)
transform = transforms.Compose([transforms.ToTensor(), # 转为张量 (C, H, W)transforms.Normalize((0.1307,), (0.3081,)) # 标准化
])# 加载数据集(已预分为训练集和测试集)
train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)# 创建 DataLoader(batch_size=64)
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True, num_workers=4)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)
batch_size=64:每批次包含 64 张图片。shuffle=True:训练时打乱数据顺序以防止过拟合。num_workers=4:使用 4 个线程并行加载数据(适用于大型数据集)。
(2) 训练循环中的批次处理
在训练过程中,每次迭代从 DataLoader 获取一个批次的数据:
for x_batch, y_batch in train_loader:# x_batch: [64, 1, 28, 28](形状为批次大小 × 通道数 × 高 × 宽)# y_batch: [64](标签)# 将数据移动到 GPU(如果可用)x_batch = x_batch.to('cuda') if x_batch.is_cuda else x_batch.to('cpu')y_batch = y_batch.to('cuda') if y_batch.is_cuda else y_batch.to('cpu')# 前向传播、计算损失、反向传播等操作...
GPU 加速:当
x_batch和y_batch被送入 GPU 后,模型的前向传播(矩阵运算)和反向传播(梯度计算)可在 GPU 上并行执行,显著提升速度。批量计算优势:GPU 同时处理 64 张图片的特征提取和分类,而非逐张处理,大幅减少计算时间。
4. 关键注意事项
显存限制:
batch size越大,单次迭代占用的显存越多。需确保显存足够(如单卡 8GB 显存可支持batch size=64,但若网络层数增加或特征维度增大,需适当减小批次)。动态调整:在资源有限时,可通过学习率衰减(如
lr_scheduler.ReduceLROnPlateau)缓解显存压力。混合精度训练:使用
torch.cuda.amp进一步优化显存使用(如半精度浮点数计算)。
5. 性能对比示例
参数 | batch size=32 | batch size=64 |
|---|---|---|
单次迭代时间 | 较高 | 较低 |
显存占用 | 较低 | 较高 |
GPU 利用率 | 中等 | 高 |
适合场景 | 小规模实验 | 大规模训练 |
总结
通过 DataLoader 将数据分批次打包(如 batch size=64),能充分利用 GPU 的并行计算能力,减少 I/O 开销,提升训练效率。实际应用中需根据硬件条件(显存大小)和任务需求动态调整批次大小,以达到最佳性能。
数据和模型需加载至同一设备(GPU/CPU),否则训练报错
在深度学习中,将数据和模型加载至同一设备(如 GPU/CPU)是确保计算正确性和效率的关键原因。以下是详细解释:
1. 计算设备的本质差异
GPU vs CPU:
GPU 擅长并行计算(如矩阵乘法),适合处理大规模数据和高维度运算(如神经网络的前向/反向传播)。
CPU 更适合低延迟、单线程任务(如逻辑判断、控制流)。
核心矛盾:若数据和模型位于不同设备,需频繁跨设备传输数据(如 CPU → GPU),显著增加计算延迟并消耗额外带宽资源。
2. 张量(Tensor)的设备属性
张量是设备感知的:每个张量(数据或参数)都明确标记其存储位置(如
x.device返回'cpu'或'cuda:0')。设备一致性要求:
模型参数(权重)和输入数据必须在同一设备上才能进行算术运算(如
model(x))。如果数据在 CPU 而模型在 GPU,运行时会触发错误(如 PyTorch 的
RuntimeError: Expected object of type torch.FloatTensor but got torch.DoubleTensor)。
3. 深度学习框架的强制校验机制
自动检查设备一致性:
框架(如 PyTorch、TensorFlow)会在运行时自动验证数据与模型的设备是否一致。
例如,PyTorch 的
nn.Module在调用forward方法时,会检查输入张量与模型参数的设备是否匹配。
- 典型错误示例:
# 错误示例:模型在 GPU,数据在 CPU model = model.to('cuda') x = torch.randn(64, 784) # x 默认在 CPU output = model(x) # 触发错误:RuntimeError: Expected all tensors to be on the same device...4. 实际训练中的效率问题
避免不必要的数据传输:
若数据和模型在同一设备(如 GPU),可直接在设备内存中完成计算,无需通过 PCIe 总线传输数据到另一设备。
跨设备传输(如 CPU → GPU)会占用网络带宽(约 5-10 GB/s),而内存带宽(GPU)可达数百 GB/s,因此保持设备一致可显著提升吞吐量。
显存优化:
大批次(batch size)的训练需更大显存支持。若强行在不同设备间分配数据和模型,可能导致显存不足或碎片化。
5. 混合精度训练的附加要求
数据类型一致性:
混合精度训练(如使用
torch.cuda.amp)要求数据和模型参数均为相同精度(如均使用float16)。若设备不同且数据类型不匹配(如模型用
fp16,数据用fp32),会导致类型转换错误或性能下降。
总结
必要性:确保数据和模型在同一设备是为了保证计算正确性和效率。
实现方式:通过
.to(device)显式指定设备(如model.to('cuda')),或在初始化时统一加载(如model = Model().to('cuda'))。容错机制:框架通过设备校验防止隐藏错误,强制开发者关注硬件兼容性问题。
前向传播
前向传播(Forward Propagation)是深度学习模型中的核心概念之一,指数据从输入层出发,经过网络各层的处理(如线性变换、激活函数),最终到达输出层并生成预测结果的过程。它是模型“推理”或“预测”阶段的体现。
前向传播的核心步骤
输入层接收数据
原始输入(如图像像素、文本向量)进入网络的第一层(输入层)。
逐层计算
每一层对输入数据进行以下操作:

输出结果
输出层的激活值即为模型的预测结果(如分类概率或回归值)。
示例:多层感知机(MLP)的前向传播
假设有一个简单的两层 MLP(输入层 → 隐藏层 → 输出层):

与反向传播的区别
前向传播:从输入到输出的单向计算,用于生成预测结果。
反向传播:从输出到输入的梯度计算,用于更新模型参数(权重、偏置)。
应用场景
分类任务:如手写数字识别(MNIST)、图像分类。
回归任务:如房价预测、时间序列预测。
生成模型:如生成对抗网络(GAN)的生成器部分。
直观理解
想象你正在搭建乐高积木:
前向传播就是按照设计图纸(模型结构)一步步组装积木,最终拼出完整的作品(预测结果)。
反向传播则是根据成品与目标的差距(损失函数),逆向调整每块积木的位置(参数优化)。
损失函数:采用交叉熵损失函数(适用于多分类任务)
交叉熵损失函数(Cross-Entropy Loss) 是深度学习中最常用的损失函数之一,尤其在 多分类任务(如图像分类、文本分类等)中占据核心地位。它通过量化预测概率分布与真实标签分布之间的差异,指导模型优化参数。以下是详细解析:
1. 什么是交叉熵?
信息论基础:交叉熵(Cross-Entropy)源于信息论,用于衡量两个概率分布之间的“距离”或“差异”。其本质是衡量模型预测结果与真实标签之间的“信息匹配程度”。
直观理解:假设你有一个骰子(6面),每次投掷结果对应一个类别。若骰子出现3的概率很高(如90%),但你实际掷出了2(真实标签),此时交叉熵会量化这种“不匹配”的损失。
2. 数学公式
对于 多分类任务,交叉熵损失函数定义为:

关键步骤:
Softmax归一化:将网络最后一层的原始输出(未归一化的分数)转换为概率分布。
例如,输入为[2, 3, -1],Softmax后变为[0.85, 0.1, 0.05]。交叉熵计算:对每个类别的概率取对数并乘以真实标签的权重(仅正确类别保留1,其余为0)。
例如,若真实标签是第2类(索引1):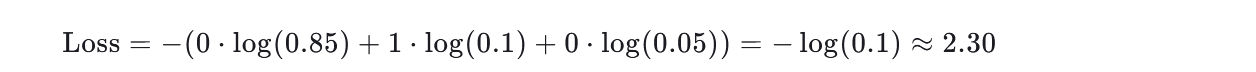
3. 为什么适用于多分类?
概率对比:通过Softmax生成的预测概率分布与真实标签分布直接对比,明确量化错误。
梯度有效性:交叉熵的梯度能高效指导参数更新,尤其是在深层网络中表现稳定。
自然适配:多分类任务中,每个样本属于单一类别(独热编码),交叉熵能精准捕捉这一特性。
4. 与二分类任务的区别

5. 优势与局限性
优势:
计算高效:对数运算加速了梯度传播,适合大规模数据。
梯度稳定:避免了均方误差(MSE)在概率接近1时的梯度消失问题。
天然适配Softmax:两者结合构成现代神经网络的标准配置(如CNN+Softmax+交叉熵)。
局限性:
类别不平衡敏感:若某些类别样本极少(如罕见病分类),需结合重采样或Focal Loss缓解。
过拟合风险:在类别高度重叠时可能导致模型过度拟合局部特征。
6. 实际应用示例
以 MNIST手写数字识别(10类)为例:
输入一张图片,网络输出10维向量(如
[0.1, 0.2, 0.7, ..., 0.05])。Softmax将其转换为概率分布
[0.1, 0.2, 0.7, ...]。若真实标签是“5”(索引4),则计算:
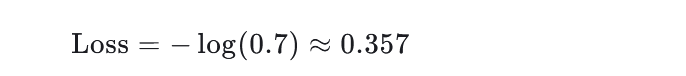
若预测错误(如概率集中在其他类别),损失值会显著增大。
7. 总结
交叉熵损失函数通过对比预测概率与真实标签的分布差异,成为多分类任务的首选工具。其与Softmax的协同作用使神经网络能够高效学习复杂模式,广泛应用于图像、语音、自然语言处理等领域。理解其原理不仅有助于构建模型,还能指导实践中的超参数调整(如学习率、批大小)和正则化策略。
反向传播:通过优化器(如SGD或Adam)计算梯度并更新权重参数。
反向传播:通过梯度下降优化神经网络
反向传播(Backpropagation)是深度学习中用于训练神经网络的核心算法,其核心思想是通过计算损失函数对模型参数的梯度,并利用优化器(如SGD、Adam)更新参数,以最小化预测误差。以下是详细解析:
1. 反向传播的核心流程
(1) 前向传播(Forward Propagation)
输入数据:从输入层出发,经过各层(如全连接层、卷积层)的线性变换和激活函数,最终生成模型预测结果(如分类概率)。
示例:输入一张28×28的手写数字图片,经过Flatten层展平为784维向量,再通过全连接层输出10维概率分布(对应0-9类)。
(2) 计算损失函数

(3) 反向传播梯度
(4) 参数更新
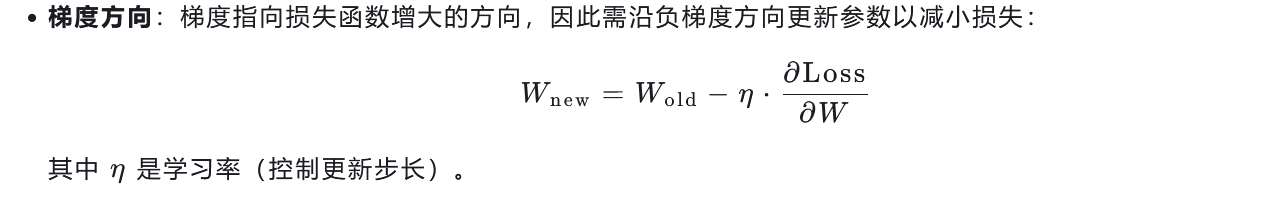
2. 优化器的作用:高效更新参数
优化器通过设计策略加速收敛并避免局部最优解,主要分为以下两类:
(1) 基于梯度的优化器
SGD(随机梯度下降):
特点:每次用单个样本或小批量数据计算梯度,更新参数。
优点:计算简单,适合大规模数据;
缺点:梯度波动大,收敛速度慢。
Momentum(动量):

(2) 自适应优化器
Adam(自适应矩估计):

3. 反向传播的实际应用示例
以MNIST手写数字识别为例:

4. 反向传播的优势与挑战
优势:

挑战:
梯度消失/爆炸:深层网络中梯度可能指数级衰减或放大,需通过初始化技巧(如Xavier初始化)缓解;
局部最优:依赖优化器的选择,需合理设置学习率和超参数。
总结
反向传播通过链式法则高效计算梯度,优化器(如SGD、Adam)则负责利用这些梯度指导参数更新。两者的结合使神经网络能够从海量数据中学习复杂模式,成为现代AI的基石。实践中需根据任务特点选择优化器(如Adam在复杂问题上表现更优),并通过调试超参数(学习率、批大小)提升训练效果。
