【高级机器学习】3. Convex Optimisation
Convex Optimisation
在机器学习中,优化问题的核心在于找到一个合适的假设 hhh,使得损失函数最小化。
这一节我们来系统介绍 凸优化 (Convex Optimisation) 的基本概念与方法。
Basics I: Convex Combination
- 给定两点 x,y∈C⊆Rdx, y \in C \subseteq \mathbb{R}^dx,y∈C⊆Rd,
如果 0≤θ≤10 \leq \theta \leq 10≤θ≤1,则
θx+(1−θ)y∈C \theta x + (1 - \theta) y \in C θx+(1−θ)y∈C
称为 凸组合 (Convex Combination)。
Basics I: Convex Set
-
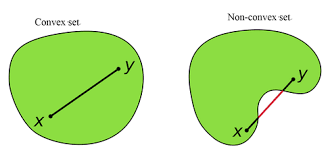
定义:集合 C⊆RdC \subseteq \mathbb{R}^dC⊆Rd 是凸集,当且仅当对任意 x,y∈Cx,y \in Cx,y∈C,以及任意 0≤θ≤10 \leq \theta \leq 10≤θ≤1,都有:
θx+(1−θ)y∈C \theta x + (1-\theta)y \in C θx+(1−θ)y∈C -
举例:
- 凸集:球、半空间、区间等
- 非凸集:环形、交错的集合等
Basics II: Convex Functions
定义
函数 f:Rd→Rf: \mathbb{R}^d \to \mathbb{R}f:Rd→R 称为凸函数,如果其定义域为凸集,且满足:
f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y),∀x,y∈domf, θ∈[0,1]
f(\theta x + (1-\theta)y) \leq \theta f(x) + (1-\theta)f(y), \quad \forall x,y \in \text{dom} f, \ \theta \in [0,1]
f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y),∀x,y∈domf, θ∈[0,1]
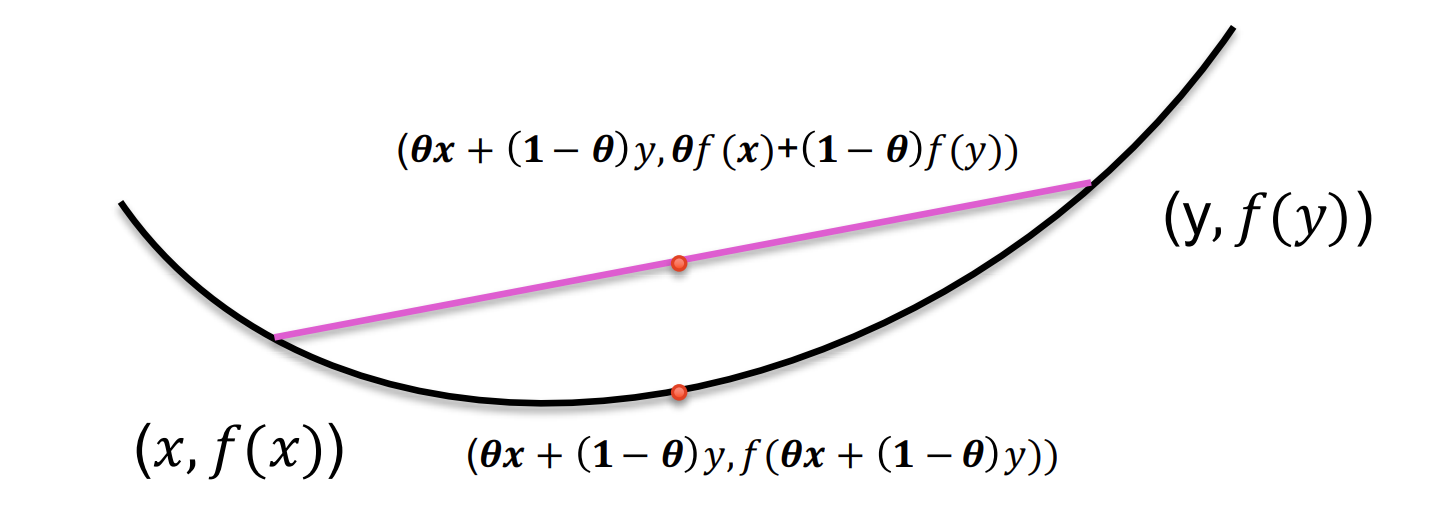
可微情况
若 fff 可微,则 fff 是凸函数当且仅当:
f(y)≥f(x)+∇f(x)⊤(y−x),∀x,y∈domf
f(y) \geq f(x) + \nabla f(x)^\top (y-x), \quad \forall x,y \in \text{dom} f
f(y)≥f(x)+∇f(x)⊤(y−x),∀x,y∈domf
其中梯度:
∇f(x)=(∂f∂x1,…,∂f∂xd)
\nabla f(x) = \left( \frac{\partial f}{\partial x_1}, \dots, \frac{\partial f}{\partial x_d} \right)
∇f(x)=(∂x1∂f,…,∂xd∂f)
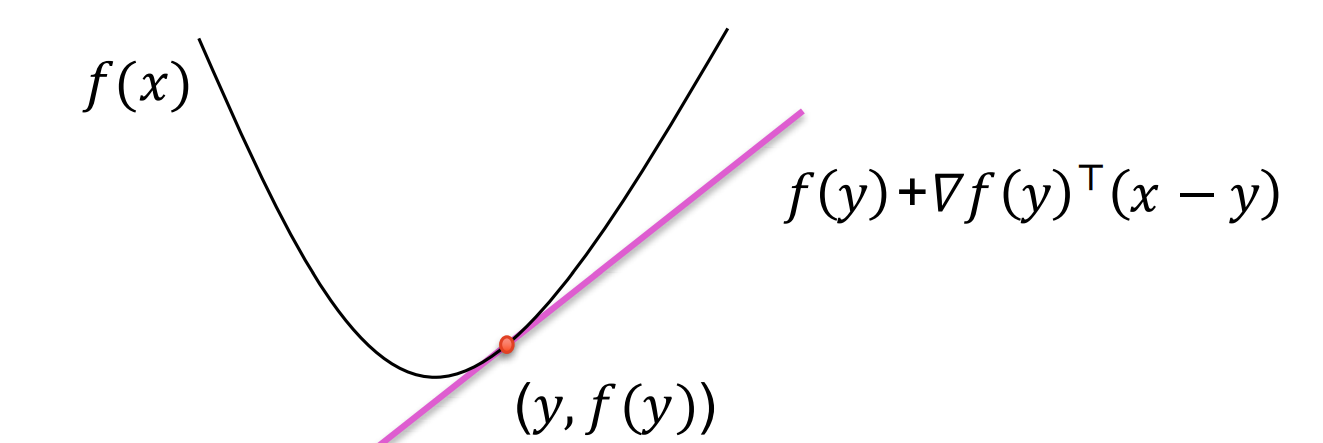
函数图像在切平面(切线)上方。
f(x)+∇f(x)⊤(y−x)f(x) + \nabla f(x)^\top (y-x)f(x)+∇f(x)⊤(y−x) 就是点 xxx 处的切线(或切平面)。
对凸函数来说,整个函数曲线都在这个切平面之上。
二阶可微情况
若 fff 二阶可微,则 fff 是凸函数当且仅当 Hessian 矩阵 半正定:
∇2f(x)⪰0,∀x∈domf
\nabla^2 f(x) \succeq 0, \quad \forall x \in \text{dom} f
∇2f(x)⪰0,∀x∈domf
等价于所有特征值非负。
Basics III: 凸函数的闭合性
-
非负加权和:若 f1,f2f_1, f_2f1,f2 是凸函数,则
f(x)=αf1(x)+βf2(x),α,β≥0 f(x) = \alpha f_1(x) + \beta f_2(x), \quad \alpha,\beta \geq 0 f(x)=αf1(x)+βf2(x),α,β≥0
仍是凸函数。 -
点对点最大值:
f(x)=max{f1(x),f2(x)} f(x) = \max \{ f_1(x), f_2(x) \} f(x)=max{f1(x),f2(x)}
也是凸函数。 -
仿射变换复合:若 fff 是凸函数,AAA 为矩阵,bbb 为向量,则
g(x)=f(Ax+b) g(x) = f(Ax + b) g(x)=f(Ax+b)
仍是凸函数。
应用:SVM 的目标函数就是凸函数。
Unconstrained Convex Optimisation
问题形式
minh∈Hf(h)=minh∈H1n∑i=1nℓ(Xi,Yi,h) \min_{h \in \mathcal{H}} f(h) = \min_{h \in \mathcal{H}} \frac{1}{n} \sum_{i=1}^n \ell(X_i, Y_i, h) h∈Hminf(h)=h∈Hminn1i=1∑nℓ(Xi,Yi,h)
其中 ℓ\ellℓ 是凸替代损失函数。
Taylor’s Theorem
若 f:R→Rf:\mathbb{R}\to\mathbb{R}f:R→R 在点 aaa 处 kkk 阶可导,则:
f(x)=f(a)+f′(a)(x−a)+⋯+f(k)(a)k!(x−a)k+hk(x)(x−a)k
f(x) = f(a) + f'(a)(x-a) + \cdots + \frac{f^{(k)}(a)}{k!}(x-a)^k + h_k(x)(x-a)^k
f(x)=f(a)+f′(a)(x−a)+⋯+k!f(k)(a)(x−a)k+hk(x)(x−a)k
其中 limx→ahk(x)=0\lim_{x \to a} h_k(x) = 0limx→ahk(x)=0。
示例
f(x)=16x3f(x) = \frac{1}{6}x^3f(x)=61x3,在 a=1a=1a=1 展开:
f(x)=16+12(x−1)+12(x−1)2+o((x−1)2),x→1
f(x) = \frac{1}{6} + \frac{1}{2}(x-1) + \frac{1}{2}(x-1)^2 + o((x-1)^2), \quad x \to 1
f(x)=61+21(x−1)+21(x−1)2+o((x−1)2),x→1
Small-o Notation
记号 f(x)=o(g(x)),x→af(x) = o(g(x)), x \to af(x)=o(g(x)),x→a 表示:
limx→af(x)g(x)=0
\lim_{x \to a} \frac{f(x)}{g(x)} = 0
x→alimg(x)f(x)=0
例如:
16x3−16−12(x−1)−12(x−1)2(x−1)2→0,x→1
\frac{\frac{1}{6}x^3 - \frac{1}{6} - \frac{1}{2}(x-1) - \frac{1}{2}(x-1)^2}{(x-1)^2} \to 0, \quad x \to 1
(x−1)261x3−61−21(x−1)−21(x−1)2→0,x→1
Gradient Descent Method
通过泰勒展开:
f(hk+1)≈f(hk)+η∇f(hk)⊤dk+o(η)
f(h_{k+1}) \approx f(h_k) + \eta \nabla f(h_k)^\top d_k + o(\eta)
f(hk+1)≈f(hk)+η∇f(hk)⊤dk+o(η)
若 ∇f(hk)⊤dk<0\nabla f(h_k)^\top d_k < 0∇f(hk)⊤dk<0,则 f(hk+1)<f(hk)f(h_{k+1}) < f(h_k)f(hk+1)<f(hk)。
- 更新公式:
hk+1=hk−η∇f(hk) h_{k+1} = h_k - \eta \nabla f(h_k) hk+1=hk−η∇f(hk)
下降方向与更新矩阵
一般形式:
hk+1=hk−ηDk∇f(hk)
h_{k+1} = h_k - \eta D_k \nabla f(h_k)
hk+1=hk−ηDk∇f(hk)
- 最速下降 (Steepest Descent):Dk=ID_k = IDk=I
- 牛顿法 (Newton’s Method):Dk=[∇2f(hk)]−1D_k = [\nabla^2 f(h_k)]^{-1}Dk=[∇2f(hk)]−1
- 常见改进:只取对角线、近似 Hessian(BFGS, L-BFGS)
学习率选择
- 精确线搜索 (Exact Line Search):η=argminηf(hk−η∇f(hk))\eta = \arg \min_\eta f(h_k - \eta \nabla f(h_k))η=argminηf(hk−η∇f(hk))
但通常计算代价太高。 - Lipschitz 光滑梯度:若存在常数 LLL 使得
∥∇f(x1)−∇f(x2)∥≤L∥x1−x2∥ \|\nabla f(x_1) - \nabla f(x_2)\| \leq L \|x_1 - x_2\| ∥∇f(x1)−∇f(x2)∥≤L∥x1−x2∥
则取 η=1L\eta = \frac{1}{L}η=L1,保证:
f(hk+1)≤f(hk)−12L∥∇f(hk)∥2 f(h_{k+1}) \leq f(h_k) - \frac{1}{2L}\|\nabla f(h_k)\|^2 f(hk+1)≤f(hk)−2L1∥∇f(hk)∥2
Gradient Convergence Rate
-
目标:找到最优解
h∗=argminh∈Hf(h) h^* = \arg \min_{h \in \mathcal{H}} f(h) h∗=argh∈Hminf(h) -
若 fff 是 强凸函数,且梯度 Lipschitz,则梯度下降具有 线性收敛率:
f(hk+1)−f(h∗)≤(1−μL)k(f(h1)−f(h∗)) f(h_{k+1}) - f(h^*) \leq \left( 1 - \frac{\mu}{L} \right)^k \left(f(h_1) - f(h^*)\right) f(hk+1)−f(h∗)≤(1−Lμ)k(f(h1)−f(h∗))
其中 μ\muμ 是强凸参数,LLL 是 Lipschitz 常数。
收敛率总结表
| 算法 | 假设 | 收敛率 |
|---|---|---|
| Gradient Descent | 光滑梯度,凸函数 | O(1/k)O(1/k)O(1/k) |
| Gradient Descent | 光滑梯度,强凸函数 | 线性收敛 (1−μ/L)k(1-\mu/L)^k(1−μ/L)k |
| Newton’s Method | 光滑梯度,强凸函数 | 二次收敛 |
Constrained Optimisation
一般的约束凸优化问题:
minh∈Hf(h),s.t. gi(h)≤0, hj(h)=0
\min_{h \in \mathcal{H}} f(h), \quad \text{s.t. } g_i(h) \leq 0, \ h_j(h) = 0
h∈Hminf(h),s.t. gi(h)≤0, hj(h)=0
- f,gif, g_if,gi 为凸函数
- hjh_jhj 为仿射函数:hj(h)=aj⊤h−bjh_j(h) = a_j^\top h - b_jhj(h)=aj⊤h−bj
这是后续学习 拉格朗日对偶性 与 KKT 条件 的基础。
