ICDE 2025 | 包含OPTIONAL和UNION表达式的SPARQL查询的高效执行方法

北京大学数据管理实验室庞悦博士关于SPARQL查询中UNION和OPTIONAL等复合操作符的优化执行的论文《Efficient Execution of SPARQL Queries with OPTIONAL and UNION Expressions》的论文被ICDE2025接收。

引言

知识图谱的激增带来了诸多RDF（Resource Description Framework，资源描述框架）数据管理问题。作为知识图谱的事实标准数据模型，RDF以<主体，谓词，客体>三元组形式表示每条边。SPARQL作为访问RDF数据集的标准查询语言，已成为大量研究的焦点。现有工作大多集中于基本图模式（Basic Graph Pattern, BGP）的执行——这是SPARQL的基础构建模块。然而，对于包含图模式运算符（如UNION和OPTIONAL）的查询执行与优化问题，学界关注则相对匮乏。

UNION和OPTIONAL表达式是SPARQL语法中的重要要素。首先，RDF数据集具有半结构化特性且不强制要求模式定义，而UNION运算符能整合多样化的信息表达方式。以从维基百科提取的开放域知识图谱DBpedia [1]为例，人物姓名可能使用谓词foaf:name或rdfs:label表示。因此，若要完整获取某类人群（如美国总统）的所有姓名记录，必须使用UNION运算符（如图1a）。

图1a

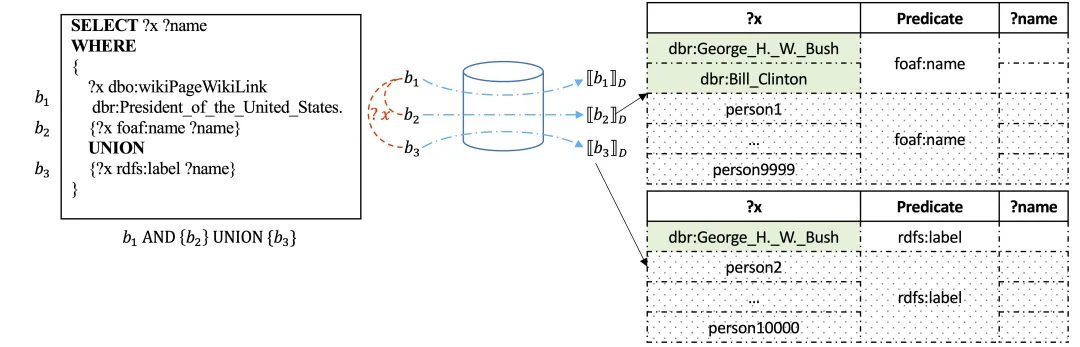
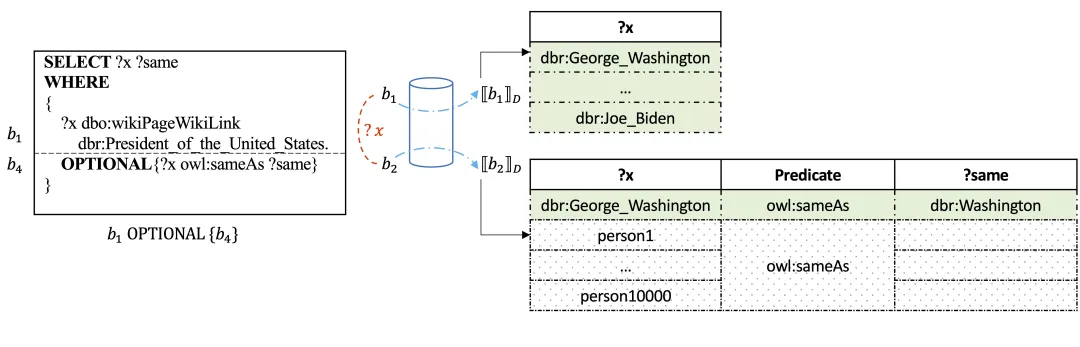
其次，RDF数据集普遍存在信息不完整性。具体而言，某些实体可能缺失同类实体通常具备的属性或关系。此时，OPTIONAL运算符便能发挥作用，它允许将部分属性或关系作为可选信息附加查询。例如，图1b中的OPTIONAL查询可获取所有美国总统记录，同时附带非同一维基百科页面的其他关联引用。由于并非每位总统在数据库中都有多重引用，包含谓词owl:sameAs的三元组被封装在OPTIONAL表达式中。

图1b

UNION和OPTIONAL表达式在实际SPARQL工作负载中被广泛应用，并已成为SPARQL 1.1标准规范的重要组成部分。最新实证研究 [2] 表明，在各类端点采集的真实SPARQL查询日志中，UNION和OPTIONAL表达式的出现频率分别达到25.10%和31.72%.

由于基本图模式（BGP）的优化执行已得到充分研究，我们选择在性能优良的BGP引擎基础上构建SPARQL-UO查询优化方案。为此，我们首先提出基于BGP的查询评估框架：具体而言，针对SPARQL-UO查询的执行计划，我们设计了一种以BGP为叶节点、图模式运算符为内部节点的树形结构——基于BGP的评估树(BE-tree)。但若直接执行BE树，某些BGP可能产生庞大的中间结果。因此，我们进一步提出基于关系代数(RA)的BE树转换方法，以生成更高效的查询计划。BE树在SPARQL查询与其关系代数执行计划之间，充当了易于构建和理解的中间表示形式。

本文提出了两种针对性的转换方法——分别处理UNION和OPTIONAL运算符的合并(merge)与注入(inject)转换。这些转换在保持查询语义的前提下（通过BE树与关系代数执行计划的一一映射实现），能够有效降低BGP、UNION和OPTIONAL运算符的执行代价。鉴于关系代数计划存在多种转换可能，我们设计了综合考虑BGP与运算符执行代价的代价模型，并选择代价削减幅度最大的转换方案。面对庞大的转换策略空间，我们采用贪心策略逐步确定转换步骤。最终生成的优化计划将由基于BGP的评估框架执行，该框架通过实时剪枝BGP评估搜索空间的查询时优化技术——候选剪枝(candidate pruning)进行增强。

前置知识：RDF数据与SPARQL查询

RDF数据

定义1（RDF数据）：设互不相交的无限集合$I$、$B$和$L$分别表示IRI、空白节点和字面量。一个RDF数据集$D$是由若干三元组构成的集合D={t1,t2,...,t∣D∣}D = \{ t_1, t_2, ..., t_{|D|\} }D={t1​,t2​,...,t∣D∣}​，其中每个三元组$t=⟨subject,property,object⟩\in (I\cup B)\times I\times (I\cup B\cup L)$.

SPARQL查询的语法

以下定义我们本文所研究的查询语言，其为SPARQL 1.1的一个真子集。假设存在一个无穷集合$V$表示查询中出现的变量，所有变量均以问号（?）开头，以此区别于IRI和字面量，因此集合$V$与$I$和$L$互不相交。本研究关注SELECT查询——这类查询通过将查询中的图模式与数据集进行匹配来获取结果。SELECT查询的基本形式为“SELECT $v_1$ $v_2$ … $v_k$ WHERE {…}”，其中SELECT子句构成查询头，WHERE子句构成查询体，如图2a所示）。SELECT子句决定了需要出现在查询结果中的投影变量，而WHERE子句则给出了需要在RDF数据集上匹配的组图模式，该组图模式可能由多种其他类型的图模式组合而成，具体定义如下。

图2a

定义2（三元组模式）：一个形如$t\in (V\cup I)\times (V\cup I)\times (V\cup I\cup L)$的三元组是一个三元组模式。

基本图模式（BGP）由一组三元组模式构成。本文重点关注连通BGP，即表示连通查询子图的BGP。为简洁起见，下文中所有提及的BGP均指连通BGP。为给出BGP的形式化定义，我们首先引入**可合并性（coalescability）**的概念。

定义3（可合并的三元组模式）：当且仅当三元组模式$t_1=⟨s_1,p_1,o_1⟩$与$t_2=⟨s_2,p_2,o_2⟩$的变量集合$s_1,o_1$和$s_2,o_2$存在至少一个共同变量时，我们称这两个三元组模式是可合并的（coalescable）。

直观地说，当两个三元组模式在主语或宾语位置上存在共同变量时，它们就具有可合并性。由于基本图模式（BGP）由多个三元组模式组成，我们可以将可合并性概念扩展到BGP层面，此时要求组成BGP的某些三元组模式之间必须满足可合并条件。

定义4（可合并的BGP）：当且仅当存在$t_{i_1}\in b_1$和$t_{i_2}\in b_2$使得$t_1$与$t_2$为可合并三元组模式时，我们称基本图模式$b_1$和$b_2$具有可合并性（coalescable）。我们将合并操作记为$+$，例如$b_1$与$b_2$合并后形成的新BGP记作$b_1+b_2$。

定义5（BGP）：BGP递归定义如下：

1. 一个三元组模式是一个BGP；
2. 如果$P_1$和$P_2$是可合并的BGP，则$P_1+P_2$是一个BGP。

定义6（图模式（Graph Pattern）、组图模式（Group Graph Pattern））：图模式递归定义如下：

1. 如果$P$是一个BGP，则$P$是一个图模式；
2. 如果$P$是一个组图模式，则$P$是一个图模式；
3. 如果$P_1$和$P_2$都是图模式，则$P_1$ AND $P_2$是一个图模式；
4. 如果$P_1$和$P_2$都是图模式，则{P1}\{P_1\}{P1​} UNION {P2}\{P_2\}{P2​}、$P_1$ OPTIONAL {P2}\{P_2\}{P2​}都是图模式。

若$P$是一个图模式，则{P}\{P\}{P}是一个组图模式。

SPARQL查询的语义

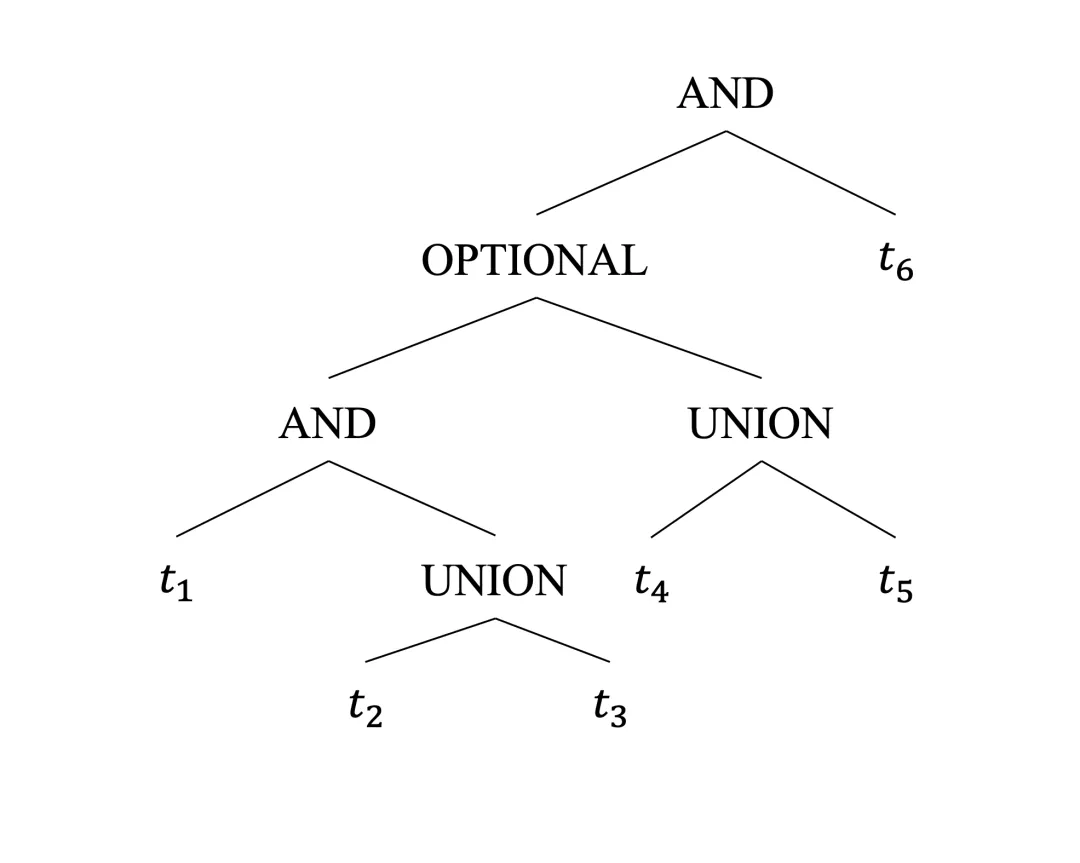
图模式本质上是由三元组模式与左结合运算符组成的表达式，这些运算符包括接受图模式作为操作数的AND、UNION和OPTIONAL。其中，AND和OPTIONAL是二元运算符，而UNION可接受两个或更多操作数。此类表达式可用树结构等价表示：每个叶节点代表一个三元组模式，每个内部节点代表一个运算符。运算符优先级决定了节点在树中的位置关系：AND $=$ OPTIONAL $\prec$ UNION。花括号会覆盖标准运算顺序并界定操作数的作用范围。图2a中的查询的树表达式展示在图2b中。

图2b

在RDF数据集$D$上匹配图模式$P$（记作$[[P]{]}_D$）会生成一个映射的多重集${\mu }_1,{\mu }_2,...,{\mu }_n$（即允许重复映射的集合）。其中，映射$\mu :V\mapsto U$是一个从变量集$V$到$(I\cup L)$的部分函数（$V$表示查询中出现的变量，$I$和$L$分别代表IRI集合和字面量集合）。映射$\mu$中出现的变量集合记作$dom(\mu )$。当且仅当对于所有变量$v\in dom({\mu }_1)\cap dom({\mu }_2)$均满足${\mu }_1(v)={\mu }_2(v)$时，称两个映射${\mu }_1$与${\mu }_2$是兼容的（记作${\mu }_1\sim {\mu }_2$）。直观而言，这意味着两个映射对共有变量的赋值必须完全一致。若${\mu }_1$与${\mu }_2$兼容，则二者的并集${\mu }_1\cup {\mu }_2$仍构成有效映射。当两者不兼容时，记作${\mu }_1\nsim {\mu }_2$。

给定两个映射的多重集${\Omega }_1$和${\Omega }_2$，它们之间存在以下几种运算：

1. Ω1⋈Ω2={μ1∪μ2 ∣ μ1∈Ω1∧μ2∈Ω2∧μ1∼μ2}{\Omega_1} \Join {\Omega_2} = \{ {\mu_1} \cup {\mu_2} \ | \ {\mu_1} \in {\Omega_1} \wedge {\mu_2} \in {\Omega_2} \wedge {\mu_1} \sim {\mu_2} \}Ω1​⋈Ω2​={μ1​∪μ2​ ∣ μ1​∈Ω1​∧μ2​∈Ω2​∧μ1​∼μ2​}
2. Ω1∪bagΩ2={μ1 ∣ μ1∈Ω1}⋃bag{μ2 ∣ μ2∈Ω2}{\Omega_1} \cup_{bag} {\Omega_2} = \{ {\mu_1} \ | \ {\mu_1} \in {\Omega_1} \} \bigcup_{bag} \{ {\mu_2} \ | \ {\mu_2} \in {\Omega_2} \}Ω1​∪bag​Ω2​={μ1​ ∣ μ1​∈Ω1​}⋃bag​{μ2​ ∣ μ2​∈Ω2​}
3. Ω1∖Ω2={μ1∈Ω1 ∣ ∀μ2∈Ω2 : μ1≁μ2}{\Omega_1} \setminus {\Omega_2} = \{{\mu_1} \in {\Omega_1}\ | \ \forall {\mu_2} \in {\Omega_2} \ : \ {\mu_1} \nsim {\mu_2} \}Ω1​∖Ω2​={μ1​∈Ω1​ ∣ ∀μ2​∈Ω2​ : μ1​≁μ2​}
4. ${\Omega }_1{\bowtie }_{\text{left}}{\Omega }_2=({\Omega }_1\bowtie {\Omega }_1){\bigcup }_{bag}({\Omega }_1\setminus {\Omega }_1)$

注意上述所有运算符都遵循多重集语义，不对运算结果去重。

以下定义如何根据 W3C 提出的 SPARQL 标准语法对图模式进行求值：

定义7（RDF数据集上图模式的求值）：图模式$P$在RDF数据集$D$上的求值（记作$[[P]{]}_D$）按如下规则递归定义，其中运算符的执行顺序遵循树表达式中的顺序：

1. 若$P$是一个三元组模式$t$，则[[P]]D={μ ∣ var(t)=dom(μ) ∧ μ(t)∈D}[[P]]_D = \{ \mu \ | \ var(t)=dom(\mu) \ \wedge \ \mu(t) \in D \}[[P]]D​={μ ∣ var(t)=dom(μ) ∧ μ(t)∈D}，其中$var(t)$表示$t$中出现的所有变量，$\mu (t)$表示所有出现在$t$中的变量都根据$\mu$替代为常量。
2. 若P={P1}P = \{P_1\}P={P1​}，则$[[P]{]}_D=[[P_1]{]}_D$。
3. 若$P=P_{1}AND{P}_2$，则$[[P]{]}_D=[[P_1]{]}_D\bowtie [[P_2]{]}_D$。
4. 若$P=P_{1}UNION{P}_2$，则$[[P]{]}_D=[[P_1]{]}_D{\bigcup }_{bag}[[P_2]{]}_D$。
5. 若$P=P_{1}OPTIONAL{P}_2$，则$[[P]{]}_D=[[P_1]{]}_D{\bowtie }_{\text{left}}[[P_2]{]}_D$。

查询计划表示形式

评估图模式$P$最直接的方法是采用树形表示法的自底向上策略。在每一步操作中，系统要么执行三元组模式匹配，要么处理运算符（包括AND、UNION或OPTIONAL）。这种基于树的求值策略严格遵循上一节讨论的SPARQL语义，但由于叶节点处每个三元组模式都会产生大量中间结果，存在固有的性能局限。以图2a中的简单SPARQL查询为例，该查询最外层的组图模式仅包含一个基本图模式(BGP)。按照树形方法，首先需要获取匹配结果$[[t_1]{]}_D$和$[[t_2]{]}_D$。显然，三元组模式$t_2$将生成大量中间结果，因为数据库中大多数人的属性都包含出生日期。

更理想的做法是将基本图模式(BGP)求值作为执行SPARQL查询的基础构建模块，并采用优化的BGP查询求值方法，例如RDF-3x [3]、SW-store [4]、gStore [5] 和 Apache Jena [6]等系统所使用的技术。因此，在我们的方法中，我们设计了一种基于BGP的求值树（BE树，BE-tree），用于表示SPARQL查询与其基于关系代数的查询计划之间的中间形式。

BE树和基于关系代数的计划结构

BE树是本文所研究SPARQL变体的一种概念上简单的语法解析树，其构建过程直观且易于理解。我们将BE树作为SPARQL查询与其基于关系代数（RA）的查询计划之间的中间表示形式。

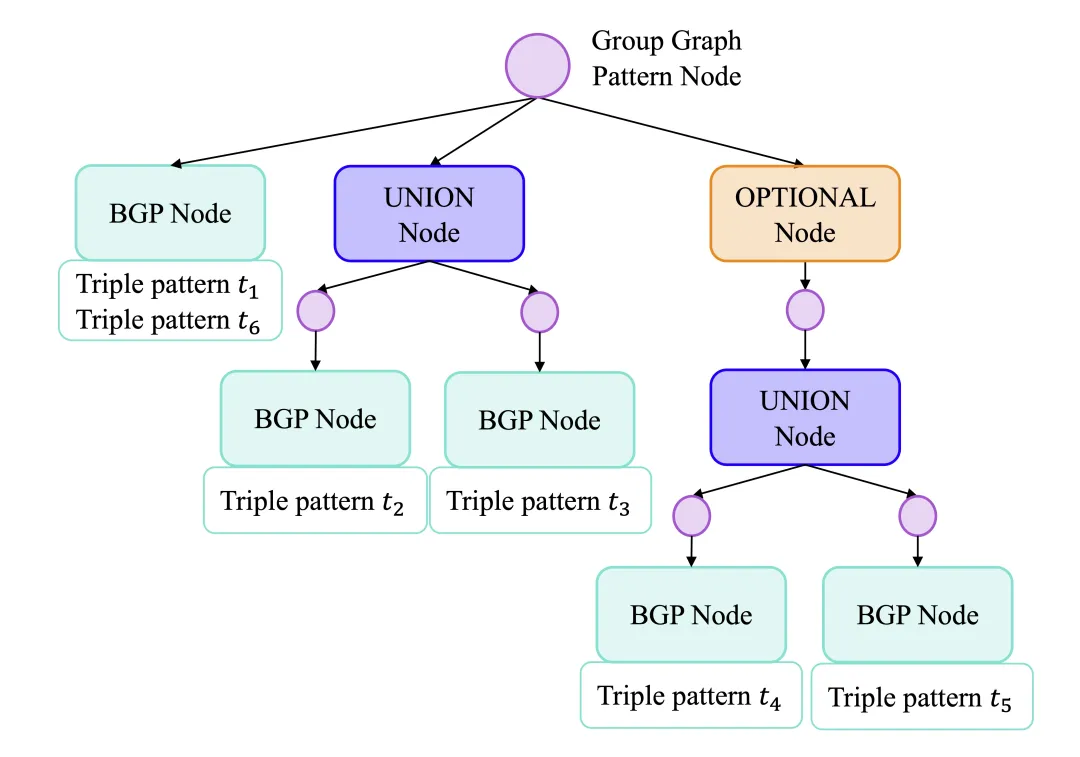
定义8（基于BGP的求值树（BE树））：给定一个组图模式$Q$，其对应的BE树$T(Q)$递归定义如下：

• $T(Q)$的根节点是表示查询$Q$的组图模式节点（定义6）；
• $T(Q)$的内部节点可为以下三类之一：UNION节点、OPTIONAL节点或组图模式节点：
  • UNION}节点表示连接两个及以上组图模式的联合表达式，其所有子节点均为组图模式节点；
  • OPTIONAL}节点表示连接左侧图模式与右侧可选图模式的表达式，该节点有且仅有一个子节点（右侧可选的组图模式节点）。
• $T(Q)$的每个叶节点均为BGP节点（定义5）。

在从SPARQL查询解析构建BE-tree后，所有父节点为组图模式节点且可合并的同层三元组模式和BGP将被合并，直到无法进一步合并为止，形成最大化的BGP。当三元组模式或BGP位于OPTIONAL节点的不同侧时，只有当该OPTIONAL是良好设计（well-designed）的 [7] 时才能合并。

作为具体示例，图2a中查询的BE树如图4所示。注意三元组模式t1和t6被合并形成一个BGP节点；其他三元组模式无法合并，因此形成单独的BGP节点。

图4

基于关系代数的计划（决定查询如何执行）定义如下：

定义9（基于关系代数的计划）：给定组图模式Q，其对应的基于关系代数的计划Plan(Q)定义如下：

• Plan(Q)的每个内部节点（包括根节点）都是AND、OPTIONAL或UNION节点
• Plan(Q)的每个叶节点都是BGP节点（定义5）

与图2b中的树表达式相比，基于关系代数的计划具有相同类型的内部节点，但叶节点是BGP而非三元组模式。为方便起见，我们将内部节点表示为图模式操作符对应的RA操作符：AND表示为⨝，UNION表示为${\cup }_{bag}$，OPTIONAL表示为${\bowtie }_{\text{left}}$。例如，图5展示了由图4的BE树转换而来的基于关系代数的计划。为了评估SPARQL查询，基于关系代数的计划以深度优先方式遍历，期间BGP被评估，它们的结果根据操作符语义组合，如算法1所示。

BE树与基于关系代数的计划转换

在前一小节中，我们直接在由查询的BE树构建的基于关系代数的计划上调用基于BGP的评估过程（算法1）。然而，通过某些保持语义的转换，可以改进查询评估的效率。

目标

我们的目标是对原始基于关系代数的计划进行转换，使生成的基于关系代数的计划具有以下属性：

• 有效性：生成的基于关系代数的计划应保持先前定义的树结构并具有相同的节点类型
• 效率：生成的基于关系代数的计划的评估应比原始基于关系代数的计划更高效

保持语义的转换

为了在保持正确性的同时优化查询执行效率，我们需要利用关于UNION和OPTIONAL的固有语义等价性，根据以下由RA支持的定理。我们首先在BE树上引入这些转换，然后将它们映射到基于关系代数的计划。

定理1：
对于任何图模式$P_1$、$P_2$、$P_3$和任何RDF数据集$D$，我们有$[[P_1\text{AND}(P_2\text{UNION}{P}_3)]{]}_D=[[(P_1\text{AND}{P}_2)\text{UNION}(P_1\text{AND}{P}_3)]!{]}_D$。

证明1：

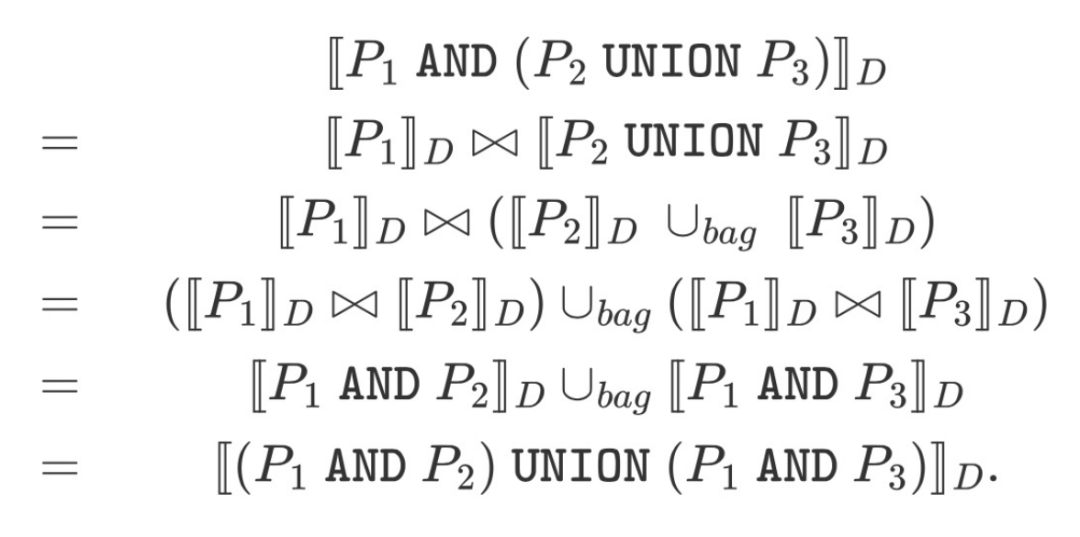
注意定理1也可扩展到具有两个以上子节点的UNION节点。

定理2：对于任何图模式$P_1$、$P_2$、$P_3$和任何RDF数据集$D$，我们有$[[P_1\text{OPTIONAL}{P}_2]{]}_D=[[P_1\text{OPTIONAL}(P_1\text{AND}{P}_2)]{]}_D$。

证明2：

这两个等价关系对应于BE树上的两种保持语义的转换：将节点与其兄弟UNION节点的子节点合并，以及将节点注入其兄弟OPTIONAL节点的子节点，定义如下。

定义10（合并转换）：当满足以下条件时，在图模式$P_1$的节点与其兄弟UNION节点（其子节点为组图模式$P_2$、$P_3$、⋯、$P_n$）上执行合并转换：

1. $P_1$是BGP节点
2. $P_2$、$P_3$、⋯、$P_n$中至少一个组图模式具有可与$P_1$合并的BGP子节点

合并转换包括以下步骤：

1. 将$P_1$插入为$P_2$、$P_3$、⋯、$P_n$的最左子节点
2. 如果可能，将$P_1$与其他BGP子节点合并，直到所有BGP节点最大化
3. 从原始位置移除$P_1$

定义11（注入转换）：当满足以下条件时，在图模式$P_1$的节点与其右侧的兄弟OPTIONAL节点（其子节点为组图模式$P_2$）上执行注入转换：

1. $P_1$是BGP节点
2. $P_2$具有可与$P_1$合并的BGP子节点

注入转换包括以下步骤：

1. 将$P_1$插入为$P_2$的最左子节点
2. 如果可能，将$P_1$与其他BGP子节点合并，直到所有BGP子节点最大化

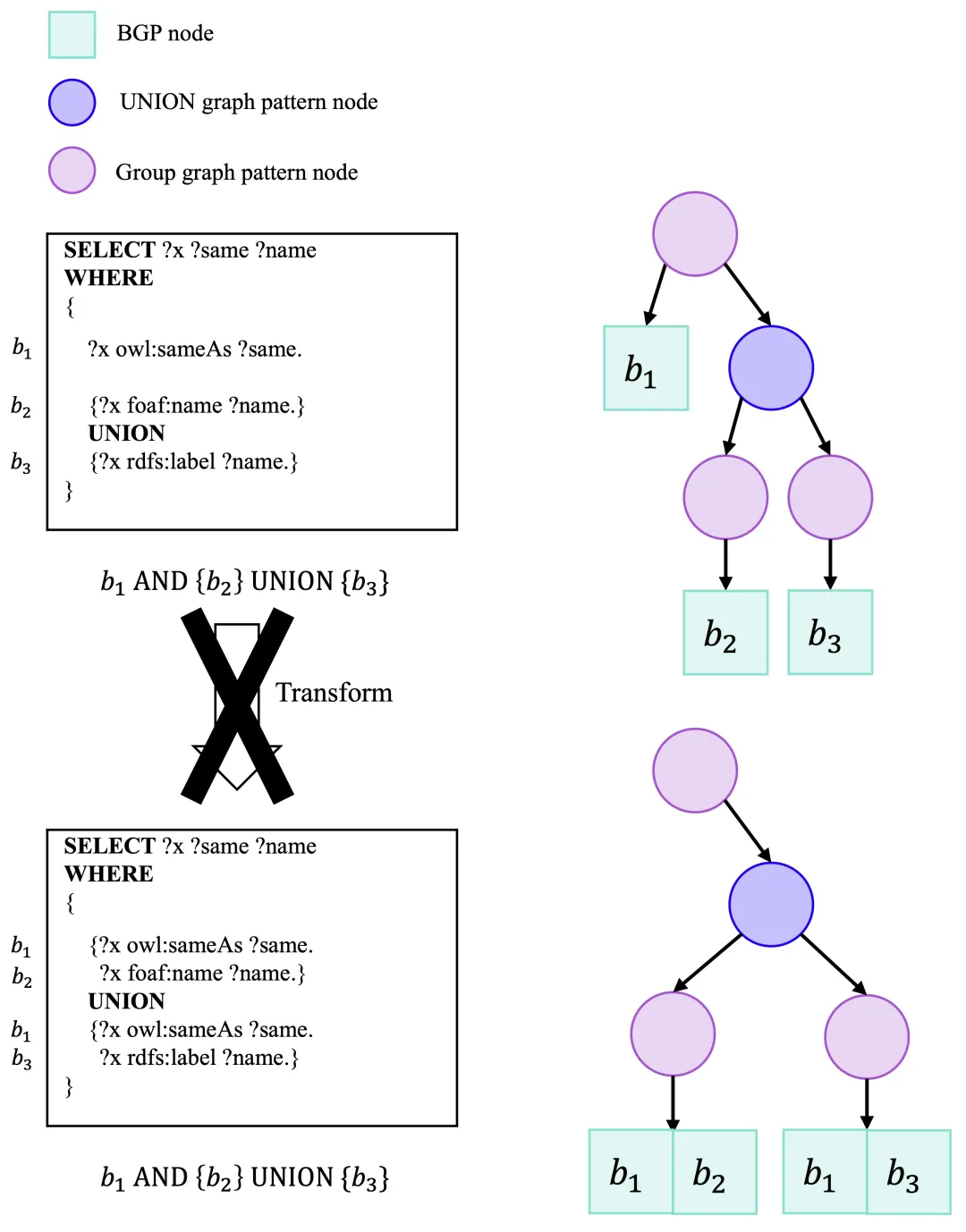
示例：在图6和图7中，我们展示了这些转换对针对DBpedia的SPARQL查询的影响。

图6

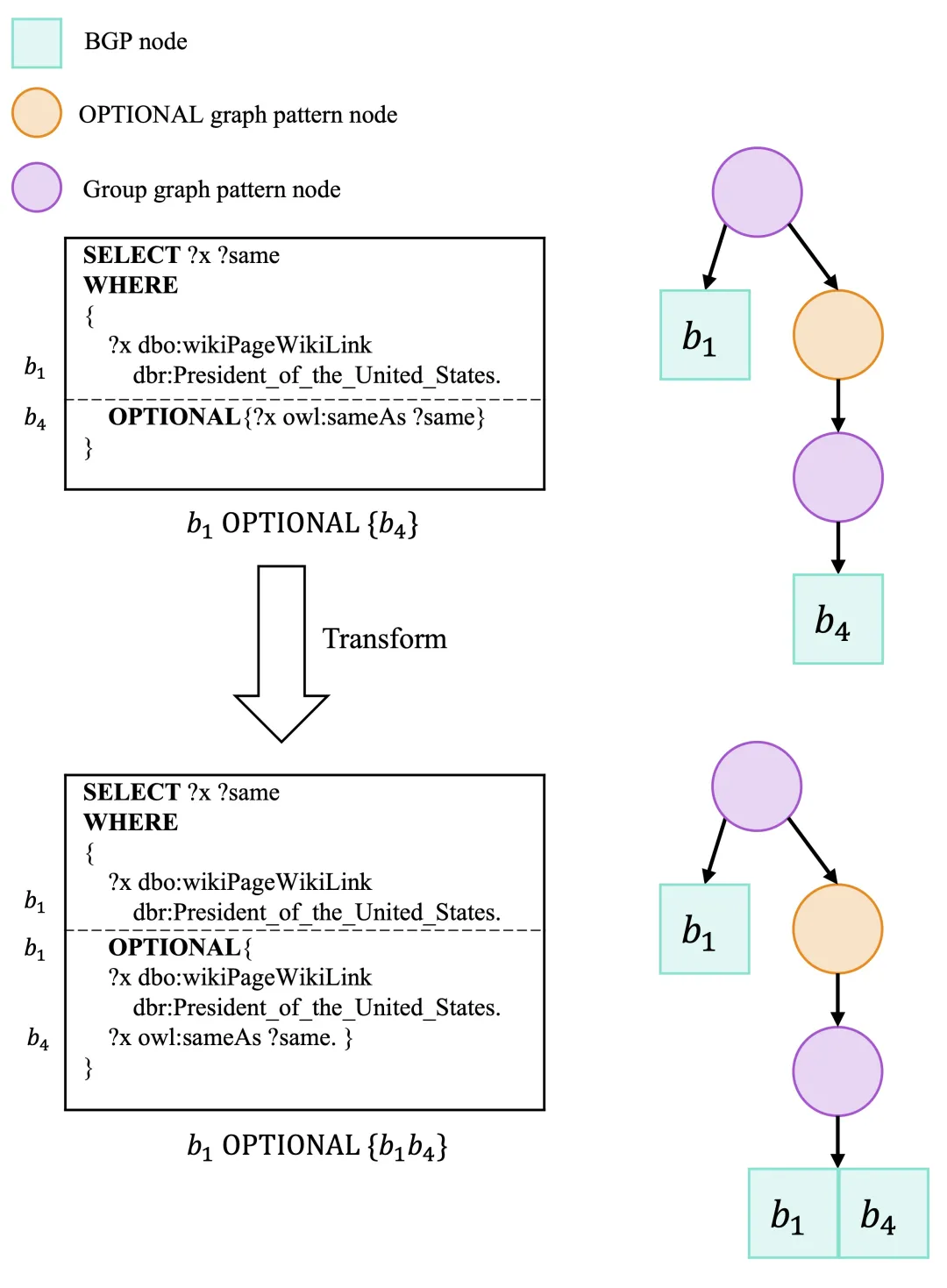
图7

在图6中，$b_4$是$b_1$右侧OPTIONAL节点的孙BGP节点，且$b_1$和$b_4$可合并。因此，可用的注入转换将$b_4$与$b_1$合并，有助于提高效率。根据原始BE树，直接评估$b_4$，并将结果与$b_1$的结果进行左外连接。由于大量实体具有表示同一现实世界对象引用间等价关系的?sameAs关系，$b_4$有许多匹配项，导致其评估和左外连接代价高昂。然而，美国总统在实体中占少数，使得$b_1$具有高选择性。注入后，我们可以依赖底层评估引擎通过选择首先评估选择性高得多的$b_1$来高效评估合并后的$b_1$$b_4$。由于$b_1$$b_4$的结果数量相比$b_4$减少，左外连接的代价也降低了。

这个例子也解释了为什么转换仅定义在可合并的BGP上。如果没有合并发生，重复评估合并或注入的BGP将产生开销。

然而，并非所有可用转换都有助于提高效率，这需要通过枚举和基于代价的选择。图7展示了对示例UNION查询可用的合并转换，将BGP $b_1$与其兄弟UNION节点合并。由于$b_1$选择性低，合并它不会加速BGP评估或减少中间结果数量，甚至由于需要两次评估而产生额外开销。

当映射到基于关系代数的计划时，转换的范围不如BE树中的兄弟节点显然。为了搜索可与BGP转换的UNION和OPTIONAL，我们需要搜索BGP的祖先，直到找到最接近根节点且不经过任何${\cup }_{bag}$节点的⨝操作符。所有从此⨝仅通过⨝可达的${\cup }_{bag}$和${\bowtie }_{\text{left}}$正是该BGP在BE树中的兄弟节点，可考虑进行转换。我们将可由BGP b考虑的${\cup }_{bag}$和${\bowtie }_{\text{left}}$集合表示为scope(b)。

基于代价的计划选择

本节将介绍一种基于代价驱动的方法，该方法通过选择预期最高效的转换操作来优化基于关系代数的查询计划。我们的代价驱动方法在高于BGP求值的层级上运作，但仍依赖于对BGP求值代价及结果规模的预估，这些数据可从底层的BGP求值引擎获取。

代价模型

SPARQL-UO代价模型

SPARQL-UO查询执行代价主要由两部分组成：评估BGP的代价和计算图模式操作符（⨝、${\cup }_{bag}$、${\bowtie }_{\text{left}}$）的代价。我们主要关注由转换引起的代价差异，称为Δ-代价。只有当Δ-代价为负时，转换才可能提升效率。下面我们将讨论如何估算Δ-代价。

合并转换的代价分析
考虑图8a所示的基于关系代数的计划。红色箭头所示的合并转换会导致以下结构变化：

1. 外层BGP将与${\cup }_{bag}$的子BGP合并
2. 如果${\cup }_{bag}$的某些子节点不是BGP或无法与外层BGP合并，则新增⨝操作连接它们
3. 转换将影响${\cup }_{bag}$的代价，因为操作数的结果规模会变化

设合并转换涉及外层BGP b和${\cup }_{bag}$节点u，u的子节点集合记为child(u)。转换前后受影响部分的代价可通过以下公式表示：

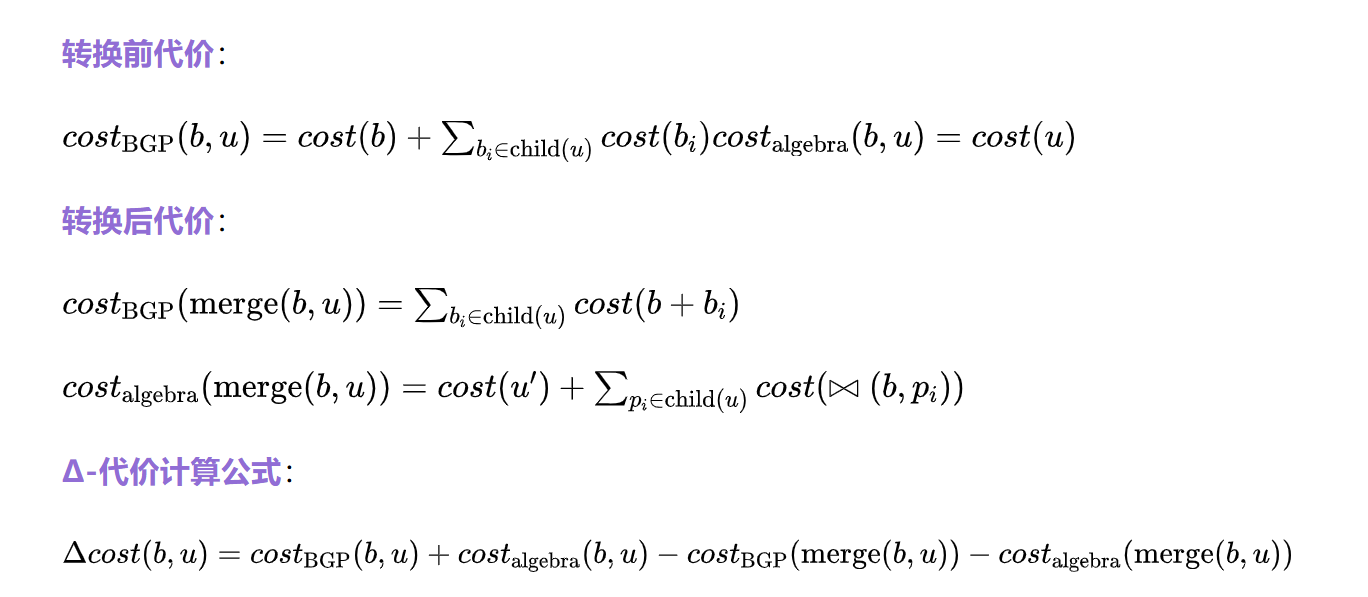
其中：

• 式(1)和(3)表示受影响BGP的代价（外层BGP b和可与b合并的子BGP $b_i$）
• 式(2)和(4)表示受影响代数操作符的代价（包括u和新引入的⨝）
• Δ-代价即为转换前后受影响部分总代价的差值

注入转换的代价分析
如图8b所示，注入转换会使${\bowtie }_{\text{left}}$节点右子树中的BGP与外层BGP合并。实践中我们选择第一个可合并的BGP作为注入目标。该转换将影响${\bowtie }_{\text{left}}$节点以及从该${\bowtie }_{\text{left}}$节点到被合并BGP路径上所有⨝的代价。

设注入转换涉及外层BGP b和${\bowtie }_{\text{left}}$节点o，代价计算公式如下：

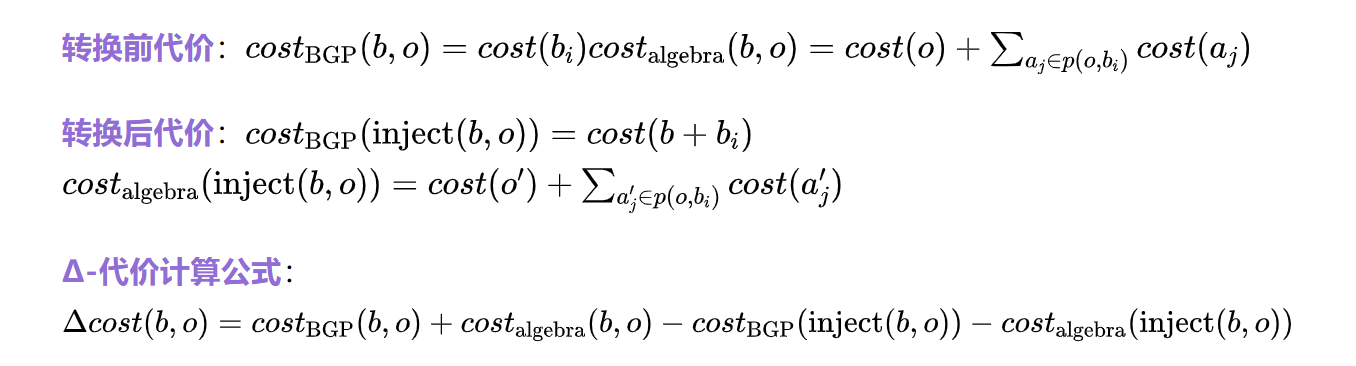
其中：

• $b_i$表示o右子树中的BGP（式6）
• $a_j$表示从${\bowtie }_{\text{left}}$到被合并BGP路径$p(o,b_i)$上的⨝操作
• $o^{\prime }$和$a_j^{\prime }$表示因基数变化导致代价改变的⋈和${\bowtie }_{\text{left}}$

基于代价的转换

本小节讨论利用上述代价模型选择转换操作的算法，以生成最高效的查询执行计划。

单个BGP转换

我们首先考虑仅涉及单个BGP的转换场景，其选择算法如算法2所示。

该算法首先在基于关系代数的计划中定位可与给定BGP进行转换的${\cup }_{bag}$和${\bowtie }_{\text{left}}$节点集合（第2行），具体方法将在下文介绍。根据定理1和2，被合并的BGP会从原始位置移除，而被注入的BGP会保留原始出现位置。这意味着一个BGP只能与一个${\cup }_{bag}$合并，但可以注入到多个${\bowtie }_{\text{left}}$节点。因此决定合并转换时，需要考察所有可行的${\cup }_{bag}$并选择Δ-代价最低的转换（第3-11行和14-17行）。而注入转换相互独立，因此我们逐个扫描${\bowtie }_{\text{left}}$节点，根据Δ-代价独立决定是否转换（第12-13行和18-22行）。

FindRelevantUO子程序说明：

1. 向上搜索仅通过⨝和${\bowtie }_{\text{left}}$可达的子树的根（第26-32行）
2. 将从根通过这些操作符可达的所有${\cup }_{bag}$或${\bowtie }_{\text{left}}$加入可行集合（第33-34行和36-43行）

处理完整基于关系代数的计划

处理包含多个BGP的完整基于关系代数的计划具有挑战性，因为不同BGP间的转换可能存在相互依赖。例如考虑组图模式{P1 OPTIONAL {P2 OPTIONAL P3}}（P1、P2和P3均为可合并BGP），存在$2^3=8$种可能的转换组合，导致计划空间随计划深度呈指数增长。

为平衡时间复杂度和转换后计划的效率，我们提出基于贪心策略的全局计划转换算法（算法3）。该算法首先对基于关系代数的计划进行拓扑排序（第1行），然后按逆拓扑序考虑BGP进行转换（第3-5行）。这确保低层BGP在高层次BGP之前完成转换，避免昂贵的回溯操作。

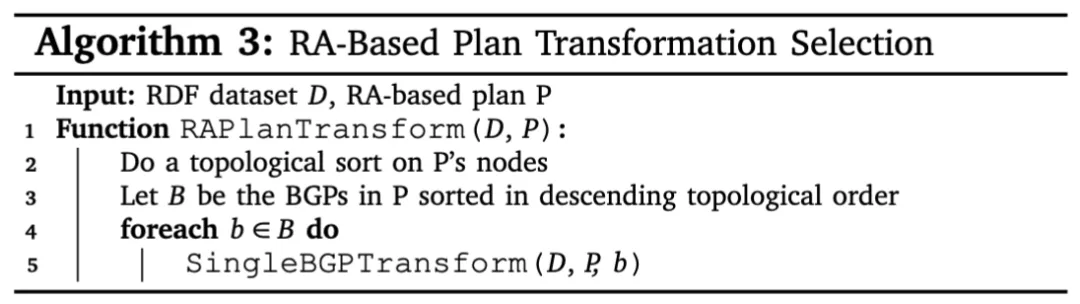
该算法通过逆向拓扑排序确保底层BGP优先转换，当发生转换时（第4行transformed标志为真），重新拓扑排序并迭代执行直到无更多优化可能（第6-8行）。这种策略有效控制了转换的复杂度，同时能获得显著的性能提升。

运行时优化：候选剪枝

在前文中，我们介绍了如何基于执行前的代价估算来选择基于关系代数的计划的转换操作。本节将提出一种称为候选剪枝（candidate pruning）的运行时优化技术。

候选剪枝的基本思想源自定理1和定理2的语义等价性。这些等价关系表明，${\cup }_{\text{bag}}$和${\bowtie }_{\text{left}}$操作符的结果受到外层图模式在公共变量上的结果约束。因此，当在查询执行过程中遇到${\cup }_{\text{bag}}$或⋈节点时，我们可以将当前公共变量上的结果设置为该节点子BGP的候选结果（candidate results）。图9通过一个OPTIONAL查询示例展示了该机制的工作原理：来自已评估图模式的变量?x的结果，将成为OPTIONAL下方组图模式的子BGP中?x的候选结果，从而剪除那些若BGP独立评估时会产生但实际无用的?x匹配项。

图9

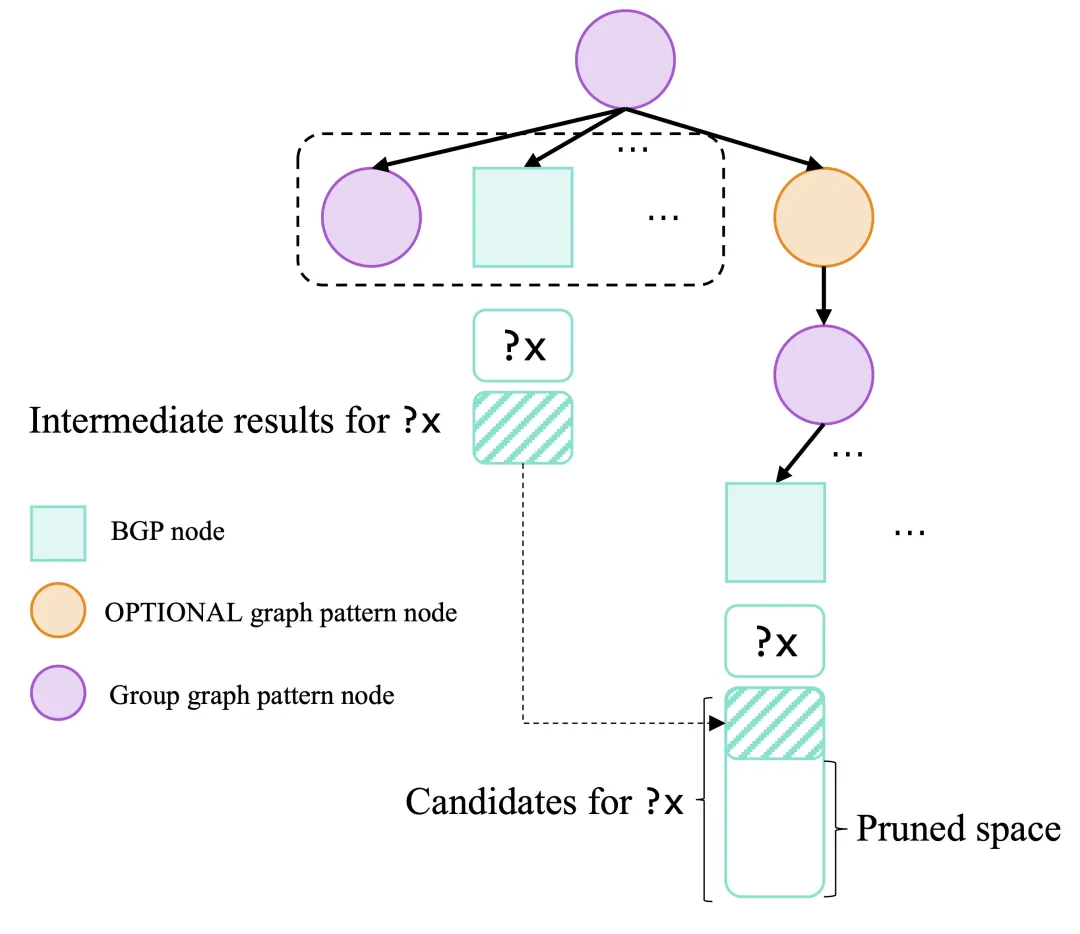
要实现有效的剪枝效果，需要确保候选结果的规模小于BGP实际结果的规模。同时，较小的候选结果规模也能降低扫描候选和设置候选的开销。为此，我们采用自适应阈值策略来控制候选结果规模：

1. 阈值设定依据：

   • 优先采用转换选择过程（算法2）中调用的BGP代价模型提供的BGP结果规模估计值作为阈值
   • 当缺乏估算数据时，基于数据集规模设置保守阈值（具体实验设置见下一节）

2. 算法增强：
   我们对算法1进行以下修改来实现候选剪枝（注意结果可通过指针传递以避免昂贵的复制操作）：

   • 为BGPBasedEvaluation函数添加第三个参数cand，表示候选结果
   • 处理${\cup }_{\text{bag}}$或${\bowtie }_{\text{left}}$节点时，将当前结果r作为第三个参数传递给BGPBasedEvaluation（算法1的第10和14行）
   • 将cand作为第三个参数传递给EvaluateBGP（算法1的第17行），仅当cand规模小于阈值时才将其设为BGP的候选结果

**树转换（执行前）与候选剪枝（运行时）**形成互补优化关系，因为树转换能够针对高选择性BGP进行合并/注入操作，分解原本因整体结果过大而无法应用候选剪枝的图模式；而候选剪枝能在执行期间跨层级传递小规模结果的剪枝效应。例如处理组图模式{P1 OPTIONAL {P2 OPTIONAL P3}}时，即使P1具有高选择性，贪心转换策略也无法将其注入P3，但P1的结果可通过P2作为候选传递给P3。在特殊情况下，当某BGP仅能与一个UNION或OPTIONAL进行转换时，对其执行转换等价于候选剪枝。此时为避免额外开销，将跳过树转换直接应用运行时剪枝。

实验评估

为验证本方法的有效性，我们在Jena、Blazegraph和gStore的BGP查询引擎上实现了基于BGP的代价感知SPARQL-UO评估策略。所有在Jena上运行的实验均启用了基于统计的优化。我们从gStore的主分支创建了独立分支，基于此实现了本文提出的SPARQL-UO优化器。实验在包含数十亿三元组的合成数据集（LUBM）和真实数据集（DBpedia、YAGO）上进行，各数据集统计信息如表1所示。所有实验在配备Intel Xeon Gold 6126处理器（2.60GHz）和256GB内存的Linux服务器上完成。

数据集	三元组数目	实体数目	谓词数目	字面量数目
LUBM	534,355,247	86,990,882	18	44,658,530
DBpedia	830,030,460	96,375,582	57,471	59,825,935
YAGO	230,677,128	99,313,763	108	153,988,292

为了验证本文提出的优化技术有效性，评估以下四种方法：

1. 基准方法（base）：直接调用基于BGP的查询评估方法（算法1）
2. 树转换方法（TT）：通过算法3转换原始基于关系代数的计划后执行算法1
3. 候选剪枝方法（CP）：在原始基于关系代数的计划上执行增强候选剪枝的算法1（候选集规模阈值为数据集三元组总数的1%）
4. 完整方法（full）：结合树转换与自适应候选剪枝阈值

由于目前缺乏专门针对SPARQL-UO查询的基准测试集，我们构建了包含真实语义和不同复杂度的微型基准测试集，包含分别在LUBM、DBpedia和YAGO上运行的6个查询。图10展示了各方法在三个数据集上的性能表现，包括执行时间以及TT和full方法执行树转换的时间，缺失柱状图表示查询出现内存不足或超时（执行时间超过$2\times 10^6$毫秒视为超时）。

图10

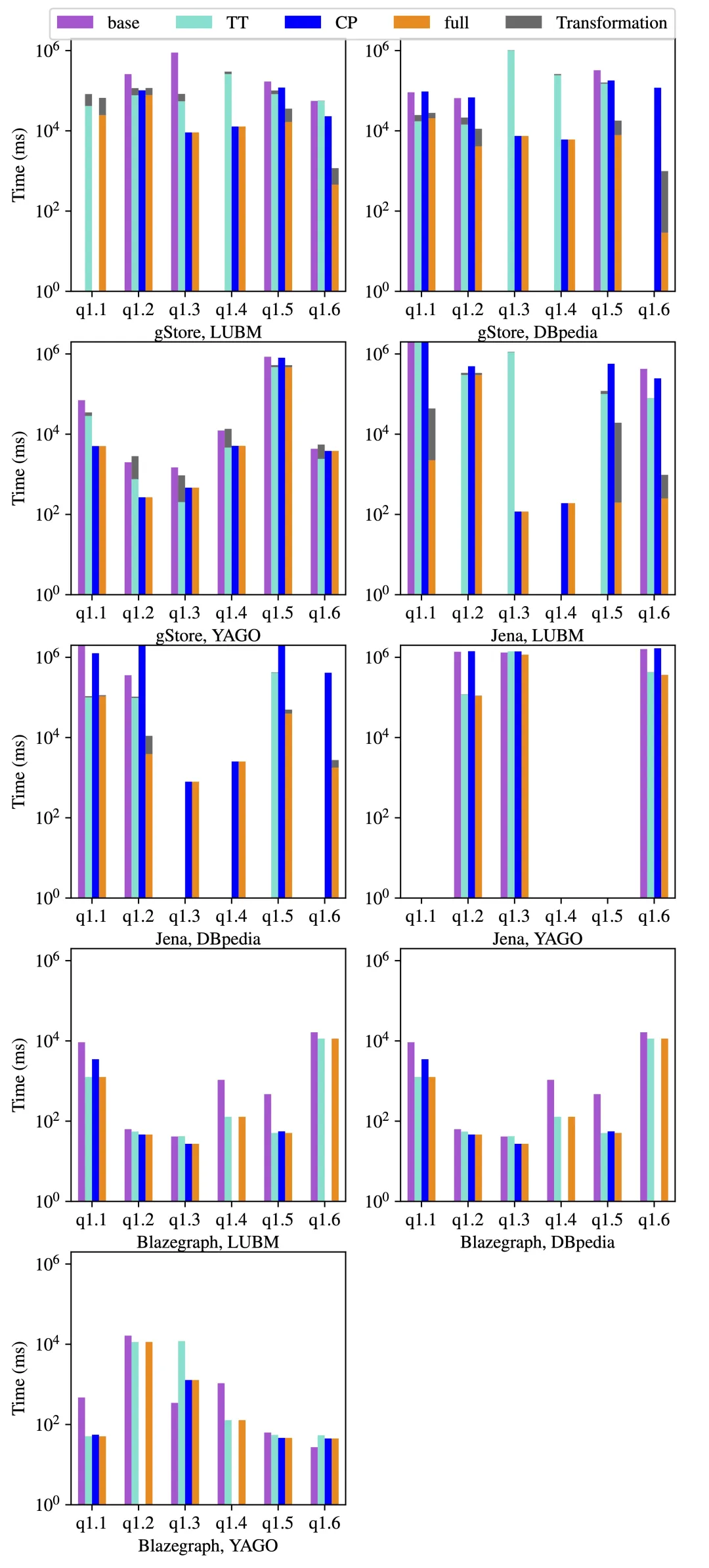
从上述实验结果中，能得到以下几点关键发现：

1. 跨系统一致性：在gStore、Jena和Blazegraph上的实验结果呈现相似趋势，证明本方法能适配不同的底层BGP执行引擎
2. 优化技术有效性：TT、CP和full在所有查询和数据集上均优于base，完整方法full在绝大多数情况下表现最优（除gStore的q1.2和Blazegraph的q1.3/q1.6外），性能提升最高达一个数量级以上，且优化方法内存消耗更低：base在24个查询中有13个出现内存不足，而full成功执行所有查询
3. 技术适用场景分析：
   • 树转换（TT）有效场景：当查询包含高选择性BGP与UNION组合时（如DBpedia的q1.1）
   • 候选剪枝（CP）有效场景：处理嵌套OPTIONAL链式查询时（如LUBM的q1.3-1.4）
   • 协同优化最佳场景：当查询同时包含高/低选择性BGP与UNION/OPTIONAL混合时（如LUBM的q1.6）

结论

知识图谱应用的蓬勃发展催生了日益增多的RDF数据管理问题。本文重点研究了如何优化包含UNION和OPTIONAL子句的SPARQL查询（简称SPARQL-UO）。通过利用现有SPARQL引擎中的BGP查询评估模块，我们提出了一系列基于代价的BGP评估树（BE树）转换方法。这些优化技术能显著减少搜索空间和中间结果规模，从而全面提升SPARQL-UO查询评估的时间和空间效率。我们在包含数十亿三元组的大规模合成与真实RDF数据集上，通过实验验证了优化方法的有效性，并与当前最优技术进行了性能对比。实验结果表明，本方法在执行效率上较现有工作有数量级的提升。

参考文献

[1] J. Lehmann, R. Isele, M. Jakob, A. Jentzsch, D. Kontokostas, P. N. Mendes, S. Hellmann, M. Morsey, P. van Kleef, S. Auer, and C. Bizer, “Dbpedia - A large-scale, multilingual knowledge base extracted from wikipedia,” Semantic Web, vol. 6, no. 2, pp. 167–195, 2015.

[2] A. Bonifati, W. Martens, and T. Timm, “An analytical study of large sparql query logs,” The VLDB Journal, vol. 29, no. 2, pp. 655–679, 2020.

[3] T. Neumann and G. Weikum, “The RDF-3X engine for scalable management of RDF data,” VLDB Journal, vol. 19, no. 1, pp. 91–113, Sep. 2009.

[4] D. J. Abadi, A. Marcus, S. Madden, and K. J. Hollenbach, “Scalable semantic web data management using vertical partitioning,” in VLDB. ACM, 2007, pp. 411–422.

[5] L. Zou, J. Mo, L. Chen, M. T. Özsu, and D. Zhao, “gstore: Answering SPARQL queries via subgraph matching,” Proc. VLDB Endow., vol. 4, no. 8, pp. 482–493, 2011.

[6] K. Wilkinson, C. Sayers, H. A. Kuno, and D. Reynolds, “Efficient RDF storage and retrieval in jena2,” in The first International Workshop on Semantic Web and Databases, 2003, pp. 131–150.

[7] J. Pérez, M. Arenas, and C. Gutierrez, “Semantics and complexity of sparql,” ACM Trans. Database Syst., vol. 34, no. 3, Sep. 2009. [Online]. Available: https://doi.org/10.1145/1567274.1567278