代码随想录刷题Day40

从中序与后序遍历序列构造二叉树

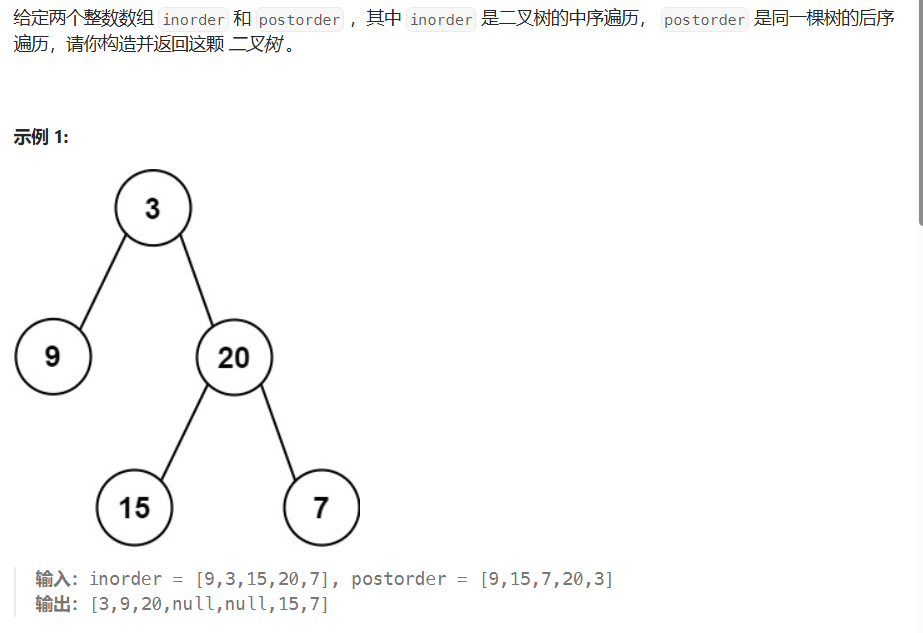
首先，得知道中序遍历和后序遍历的特点：        

• 中序遍历是：左中右
• 后序遍历是：左右中

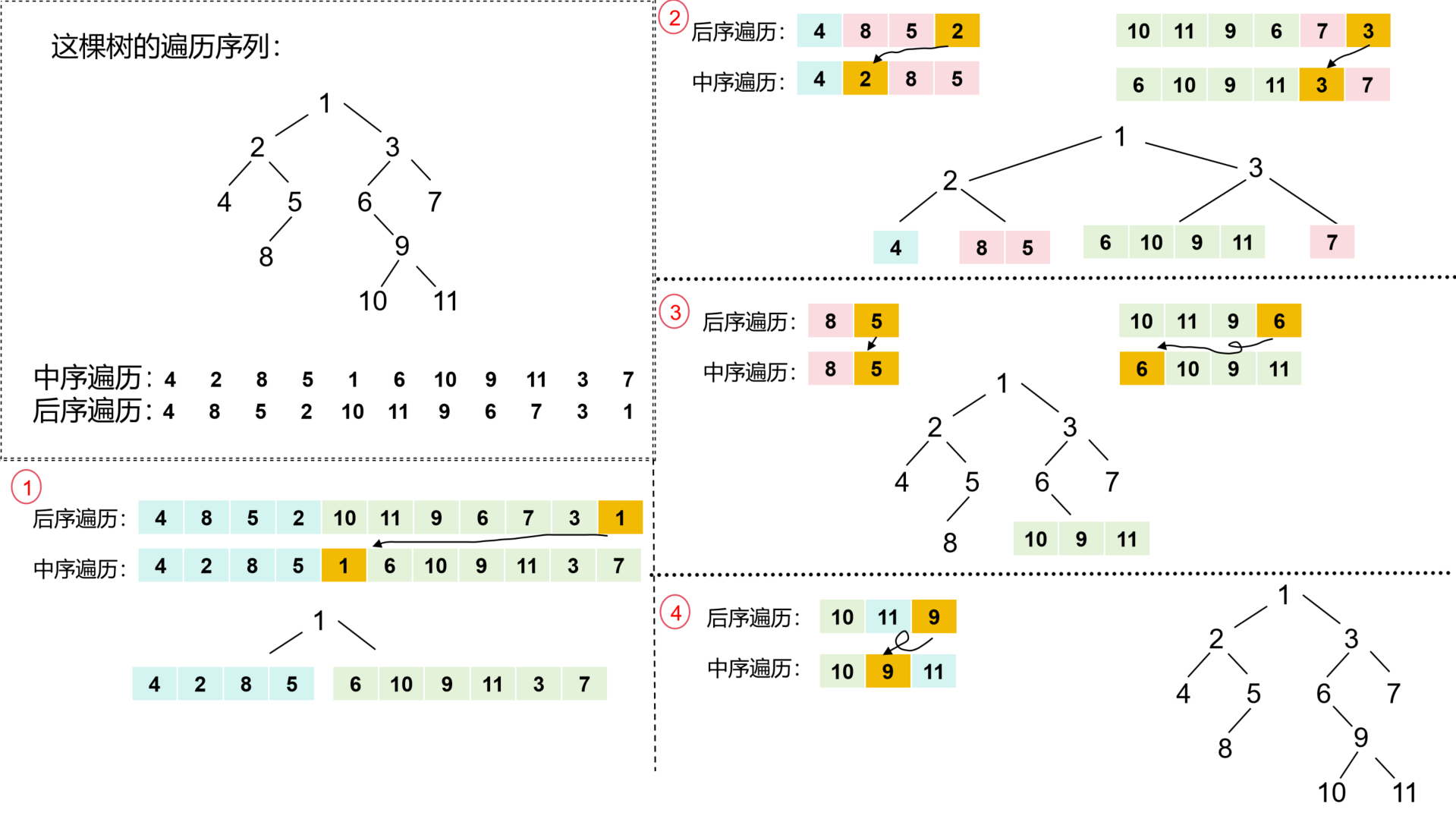
这道题的大致思路：

1. 后序遍历的最后一个值是“中”也就是一棵树的根节点。
2. 找到“中”后，再去中序遍历结果中找出左子树的序列长度和中序遍历序列，以及右子树的中序遍历序列。
3. 左子树的中序遍历的序列长度会和后序遍历长度一样，所以可以从后序遍历结果中接着提取左子树的后序遍历序列和右子树后序遍历序列。
4. 以“中”的值以及递归创建的左右子树的指针创建一棵树并返回。

代码（这份代码是最初的思路，并不是最高效的方式，因为每一次递归都会创建4个向量，最直接的方式其实是原地扫描两个序列向量，只需要传递下标值就好）：

class Solution {
public:TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int len = postorder.size();//递归的终点状态是节点为空if(len == 0 ) return nullptr;int left_size;//后序的最后一个节点是“左右中”的中，在中序遍历里找到该节点int mid_val = postorder[len-1];//确定左子树的序列范围for(int i = 0;i<len;i++){if(inorder[i]==mid_val){left_size = i;break;}}//确定左右子树的中序遍历和后序遍历序列vector<int> left_inorder(inorder.begin(),inorder.begin()+left_size);vector<int> left_postorder(postorder.begin(),postorder.begin()+left_size);vector<int> right_inorder(inorder.begin()+left_size+1,inorder.end());vector<int> right_postorder(postorder.begin()+left_size,postorder.end()-1);//递归创建左右子树，左右子树的序列范围是一样的长度return new TreeNode(mid_val,buildTree(left_inorder,left_postorder),buildTree(right_inorder,right_postorder));}
};

最大的二叉树

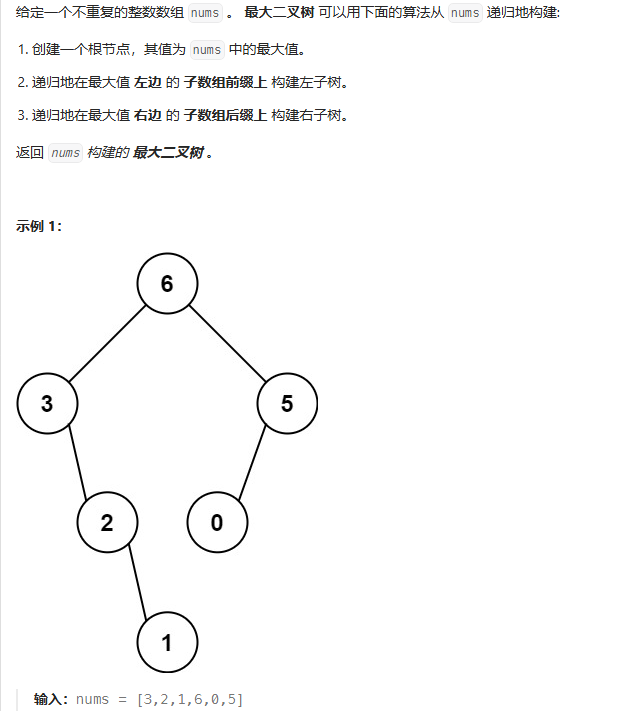
这道题的思路类似上一题递归构建树的方式：

1. 先找到根节点：最大值
2. 确定左子树的序列和右子树的序列
3. 递归构建左右子树，并返回构建好的树的地址

代码：

class Solution {
public:TreeNode* constructMaximumBinaryTree(vector<int>& nums) {int len = nums.size();if(len ==0) return nullptr;int max_val = nums[0];int max_index = 0;//确定根：数组的最大值for(int i = 0;i<len;i++){if(max_val < nums[i]){max_val = nums[i];max_index = i;}}//递归构建左右子树，并返回新的树vector<int> left_nums(nums.begin(),nums.begin()+max_index);vector<int> right_nums(nums.begin()+max_index+1,nums.end());return new TreeNode(max_val,constructMaximumBinaryTree(left_nums),constructMaximumBinaryTree(right_nums));}
};

小结一下，这两道题的思路差不多一致，都是先找出根节点，左子树序列，右子树序列，然后递归生成树。