当前位置：首页 > ai >正文

【AlphaFold3】网络架构篇（7）| 详解Diffusion training set-up

ai 2025/7/31 10:35:14

在这里插入图片描述

博主简介：努力学习的22级计算机科学与技术本科生一枚🌸
博主主页： @Yaoyao2024
往期回顾：【AlphaFold3】网络架构篇（6）|Diffusion Module讲解
每日一言🌼: 不飞则已，一飞冲天；不鸣则已，一鸣惊人。——《韩非子》🌺

一、扩散训练

翻译：

我们的扩散训练方法在很大程度上遵循文献¹，但存在一些显著差异，主要体现在损失函数上。

为提高训练效率，我们使用比主干网络更大的批量大小（batchsize)来训练扩散模块（见主文章图2c）。具体实现方式是：先运行一次主干网络，然后根据算法19通过随机旋转和平移生成48个版本的输入结构(对ground-truth进行增强），并为每个结构添加独立噪声。之后，我们在所有这些结构上并行训练扩散模块。这种方式效率很高，因为扩散模块的计算成本远低于模型主干。
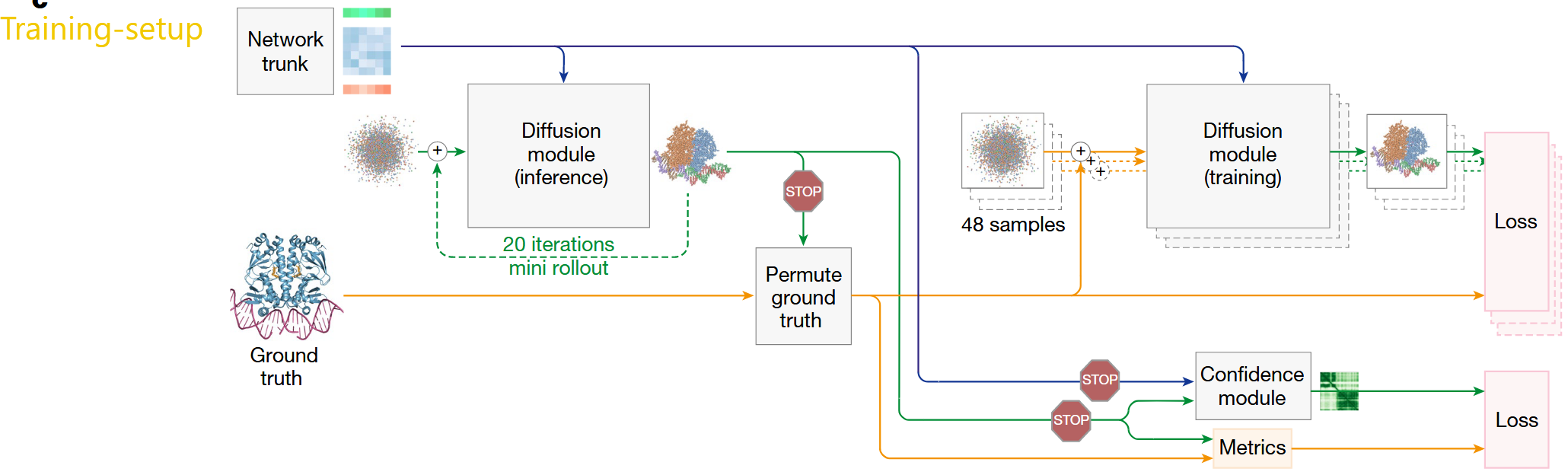
在这里插入图片描述

我们对扩散模块输出的去噪结构应用加权对齐MSE损失（weighted aligned MSE loss）。首先，将真实结构 $x⃗lGT\vec{\mathrm{x}}_{l}^{\mathrm{GT}}$ )刚性对齐到去噪结构 $x⃗l\vec{\mathbf{x}}_{l}$ ，公式如下：
$align({x⃗lGT},{x⃗l)},{wl})(2)\{\vec{\mathbf{x}}_{l}^{{\mathrm{GT-aligned}}}\}=\text{weighted rigid align}(\{\vec{\mathbf{x}}_{l}^{{\mathrm{GT}}}\},\{\vec{\mathbf{x}}_{l})\},\{w_{l}\})\text{(2)}$
其中权重 $w_{l}$ 由公式（4）给出。然后计算加权MSE损失：
$LMSE=13mean⁡l(wl∣∣x⃗l−x⃗lGT-aligned∣∣2),(3)\mathcal{L}_{{\mathrm{MSE}}}=\frac{1}{3}\operatorname*{mean}_{l}\left(w_{l}||\vec{\mathbf{x}}_{l}-\vec{\mathbf{x}}_{l}^{\text{GT-aligned}}||^{2}\right),\quad(3)$
其中对核酸和配体原子的权重进行了提升，具体为：
$wl=1+flis_dnaαdna+flis_maαma+flis_ligandαligandw_l=1+\mathrm{f}_l^{\mathrm{~is\_dna}}\alpha^{\mathrm{dna}}+\mathrm{f}_l^{\mathrm{~is\_ma}}\alpha^{\mathrm{~ma}}+\mathrm{f}_l^{\mathrm{~is\_ligand}}\alpha^{\mathrm{~ligand}}$
超参数设置为 $αdna=αrna=5,andαligand=10\alpha^{\mathrm{dna}}=\alpha^{\mathrm{rna}}=5,\mathrm{and~}\alpha^{\mathrm{ligand}}=10$ 。

为确保成键配体（包括成键聚糖）的键长正确，我们在微调阶段引入了一个辅助损失：
$Lbond=mean⁡(l,m)∈B(∥x⃗l−x⃗m∥−∥x⃗lGT−x⃗mGT∥)2,(5)\mathcal{L}_{\mathrm{bond}}=\operatorname*{mean}_{(l,m)\in\mathcal{B}}\left(\left\|\vec{\mathrm{x}}_l-\vec{\mathrm{x}}_m\right\|-\left\|\vec{\mathrm{x}}_l^{\mathrm{GT}}-\vec{\mathrm{x}}_m^{\mathrm{GT}}\right\|\right)^2,\quad(5)$
其中 $B\mathcal{B}$ 是定义成键配体与其母链之间化学键的原子对集合（起始原子索引，结束原子索引）。

我们还应用了基于平滑LDDT的辅助结构损失，如算法27所述。扩散模块的最终损失为：
$Ldiffusion=(t^2+σdata2)/(t^+σdata)2⋅(LMSE+αbond⋅Lbond)+Lsmoothlddt，（6）\mathcal{L}_{\mathbf{diffusion}}=(\hat{t}^2+\sigma_{\mathbf{data}}^2)/(\hat{t}+\sigma_{\mathbf{data}})^2\cdot(\mathcal{L}_{\mathbf{MSE}}+\alpha_{bond}\cdot\mathcal{L}_{\mathbf{bond}})+\mathcal{L}_{\mathbf{smooth_lddt}} ，（6）$
其中 $t^\widehat{t}$ 是采样的噪声水平， $σdata\sigma_{\mathrm{data}}$ 是由数据方差决定的常数（设为16）， $αbond\alpha_{bond}$ 在常规训练中为0，在两个微调阶段均为1。在计算这些损失之前，我们按照4.2节所述应用最优真实链分配。

训练期间，噪声水平(noise level）从 $σdata⋅exp⁡(−1.2+1.5⋅N(0,1))\sigma_{\mathrm{data}}\cdot\exp(-1.2+1.5\cdot\mathcal{N}(0,1))$ 中采样；推理期间，噪声调度定义为：
$t^=σdata⋅(smax1/p+t⋅(smin1/p−smax1/p))p(7)\hat{t}=\sigma_{\mathrm{data}}\cdot(s_{\mathrm{max}}^{1/p}+t\cdot(s_{\mathrm{min}}^{1/p}-s_{\mathrm{max}}^{1/p}))^p\quad(7)$ 其中 $smax⁡=160,smin⁡=4⋅10−4,p=7s_{\max}=160,s_{\min}=4\cdot10^{-4},p=7$ ， $t$ 在 $[0, 1]$ 上均匀分布，步长为 $1200.\frac1{200}.$

讲解：

🪧一、核心目标：训练扩散模块生成高精度原子坐标

扩散训练的核心是通过优化损失函数，让扩散模块（Algorithm 20）学会从带噪声的原子位置中恢复真实结构。与传统训练相比，本节的训练方法在效率优化和损失设计上有显著创新，尤其针对多分子类型（蛋白质、核酸、配体）的结构预测进行了适配。

🪧二、训练效率优化：批量扩展策略
为解决扩散模块训练耗时的问题，文中采用了“主干网络单次运行+多版本数据增强”的策略：

主干网络复用：先运行一次主干网络（生成strunk_i、ztrunk_ij等特征），避免重复计算（主干网络成本高）；
数据增强生成多版本：基于算法19（中心随机增强），对同一输入的ground-truth结构进行48次随机旋转、平移，并添加独立噪声，生成48个带噪声的结构版本；
并行训练：扩散模块在48个版本上并行训练，充分利用计算资源（扩散模块成本低）。

优势：在不增加主干网络计算量的前提下，将批量大小扩大48倍，加速训练收敛。

🪧 三、核心损失函数设计

扩散训练的损失由三部分组成：加权对齐MSE损失、键长辅助损失、平滑LDDT损失，最终通过公式（6）组合。

1. 加权对齐MSE损失 $LMSE\mathcal{L}_{\mathrm{MSE}}$ ：基础位置损失

作用：衡量去噪结构与真实结构的位置差异，是最核心的损失项。
关键步骤：
- 刚性对齐（公式2）：通过weighted_rigid_align（算法28）将真实结构对齐到预测的去噪结构，消除全局旋转、平移的影响（因为分子结构的绝对位置不重要，相对位置才关键）。
- 加权计算（公式3-4）：对不同类型原子赋予不同权重：
  - 蛋白质原子权重为1；
  - 核酸（DNA/RNA）原子权重为(1+5=6)；
  - 配体原子权重为(1+10=11)。
- 设计动机：核酸和配体的结构数据相对稀缺，通过提高权重强制模型更关注这些难预测的原子，提升其预测精度。

2. 键长辅助损失 $Lbond\mathcal{L}_{\mathrm{bond}}$ ：确保化学键长度正确

作用：针对成键配体（如配体与蛋白质之间的共价键、聚糖的糖苷键），约束其键长与真实结构一致。
计算逻辑（公式5）：对所有成键原子对 $(l, m)$ ，计算预测键长（ $x⃗l−x⃗m\vec{x}_l - \vec{x}_m$ ）与真实键长（ $x⃗GT,l−x⃗GT,m\vec{x}_{\text{GT}, l} - \vec{x}_{\text{GT}, m}$ ）的平方差，取均值。
适用阶段：仅在微调阶段启用（ $αbond=1\alpha_{\text{bond}}=1$ ），避免训练初期因噪声大导致键长约束失效。

3. 平滑LDDT损失（ $Lsmooth_lddtL_{\text{smooth\_lddt}}$ ）：衡量全局结构相似性

LDDT（Local Distance Difference Test）是评估蛋白质结构预测精度的经典指标，平滑LDDT损失通过原子对距离差异衡量全局结构相似性，算法27解析：

步骤1-2：计算所有原子对的预测距离（ $δxlm\delta x_{lm}$ ）和真实距离（ $δxGT,lm\delta x_{\text{GT}, lm}$ ）；
步骤3-4：计算距离差异 $δlm\delta_{lm}$ ，并通过4个sigmoid函数的平均（ $ϵlm\epsilon_{lm}$ ）将差异转换为“相似性得分”（差异越小， $ϵlm\epsilon_{lm}$ 越接近1）；
步骤5-6：定义“包含半径”：核酸原子对仅考虑真实距离<30Å的对，其他原子（如蛋白质）仅考虑<15Å的对（过滤无关远距原子对，聚焦局部结构）；
步骤7-8：计算加权平均相似性得分（lddt），损失为 $\text{lddt}$ （得分越低，损失越大）。

优势：相比MSE更关注局部结构相似性，对全局结构的整体一致性更敏感。

4. 最终损失组合（公式6）

$Ldiffusion=t^2+σdata2(t^+σdata)2⏟噪声水平权重⋅(LMSE+αbond⋅Lbond)+Lsmooth_lddtL_{\text{diffusion}} = \underbrace{\frac{\hat{t}^2 + \sigma_{\text{data}}^2}{(\hat{t} + \sigma_{\text{data}})^2}}_{\text{噪声水平权重}} \cdot (L_{\text{MSE}} + \alpha_{\text{bond}} \cdot L_{\text{bond}}) + L_{\text{smooth\_lddt}}$

噪声水平权重： $t^\hat{t}$ （当前噪声水平）越大，权重越大，强制模型在高噪声阶段更关注MSE损失（优先恢复大致结构）；低噪声阶段权重减小，平衡LDDT损失（优化细节）。
平衡多目标：同时优化位置精度（MSE）、键长正确性（ $LbondL_{\text{bond}}$ ）和全局结构相似性（ $Lsmooth_lddtL_{\text{smooth\_lddt}}$ ）。

🪧 四、噪声设置：训练与推理的差异

训练时：噪声水平从 $σdata⋅exp⁡(−1.2+1.5⋅N(0,1))\sigma_{\text{data}} \cdot \exp(-1.2 + 1.5 \cdot \mathcal{N}(0, 1))$ 采样，覆盖宽范围噪声（模拟不同去噪阶段）；
推理时：噪声调度通过公式（7）生成，从高噪声（ $smax=160s_{\text{max}}=160$ ）到低噪声（ $smin=4e−4s_{\text{min}}=4e-4$ ）平滑衰减，共200步（确保去噪过程稳定收敛）。

讲解：关键算法解析

👉🏻 算法27（平滑LDDT损失）：

在这里插入图片描述

SmoothLDDTLoss 是用于评估预测原子结构与真实结构局部相似性的损失函数，核心通过原子对距离差异衡量结构质量，适配核酸（DNA/RNA）与非核酸分子的差异。

1. 计算所有原子对的距离（步骤1-2）

作用：计算预测结构和真实结构中，每一对原子 (l, m) 的三维欧氏距离。
细节：
- $δxlm\delta x_{lm}$ ：预测结构中原子 l 和 m 的距离；
- $δxlmGT\delta x_{lm}^{\mathrm{GT}}$ ：真实结构中原子 l 和m 的距离；
- 遍历所有原子对（包括 l≠m，因为 l=m 时距离为0，无意义）。

2. 计算距离差异与平滑得分（步骤3-4）

步骤3：计算预测与真实结构的距离差异 $δlm\delta_{lm}$ （绝对值，确保非负）。差异越小，结构越相似。
步骤4：通过4个Sigmoid函数的平均，将 $δlm\delta_{lm}$ 转换为平滑相似性得分 $ϵlm\epsilon_{lm}$ ：
- Sigmoid函数形状：输入越小（距离差异小），输出越接近1；输入越大（距离差异大），输出越接近0。
- 4个阈值（0.5、1、2、4 Å）覆盖“小差异→大差异”的区间，让得分对不同尺度的差异更鲁棒。
- 平均4个Sigmoid输出，得到最终的平滑得分 $ϵlm\epsilon_{lm}$ （取值范围：0~1，越接近1表示结构越相似）。

3. 定义“有效原子对”的包含半径（步骤5-6）

步骤5：标记原子是否属于核酸（nucleotide）（DNA或RNA）：f_is_nucleotide_l = 1 表示原子 l 是核酸原子，否则为0。
步骤6：根据原子类型（核酸/非核酸），定义有效距离阈值：
- 若原子对属于核酸（ $flis_nucleotide=1f_l^\mathrm{is\_nucleotide} = 1$ ）：仅考虑真实距离 < 30 Å 的原子对（核酸结构更“舒展”，长距离对也有意义）；
- 若原子对属于非核酸（如蛋白质， $flis_nucleotide=0f_l^\mathrm{is\_nucleotide} = 0$ ）：仅考虑真实距离 < 15 Å 的原子对（蛋白质局部结构更关键，短距离对足够）；
- $c_{lm}$ 是布尔值（0或1）：标记该原子对是否属于“有效对”，用于后续计算。

4. 计算最终LDDT得分与损失（步骤7-8）

步骤7：计算有效原子对的加权平均相似性：
- 分子：有效原子对（c_lm=1）的平滑得分 ϵ_lm 加权和；
- 分母：有效原子对的数量（c_lm=1 的总对数）；
- 最终 lddt 是“有效原子对的平均相似性得分”（取值范围：0~1，越接近1表示结构越准）。
步骤8：损失定义为 1 - lddt：得分越高（结构越准），损失越小；反之则损失越大，需反向优化。

👉🏻 算法28（加权刚性对齐）：

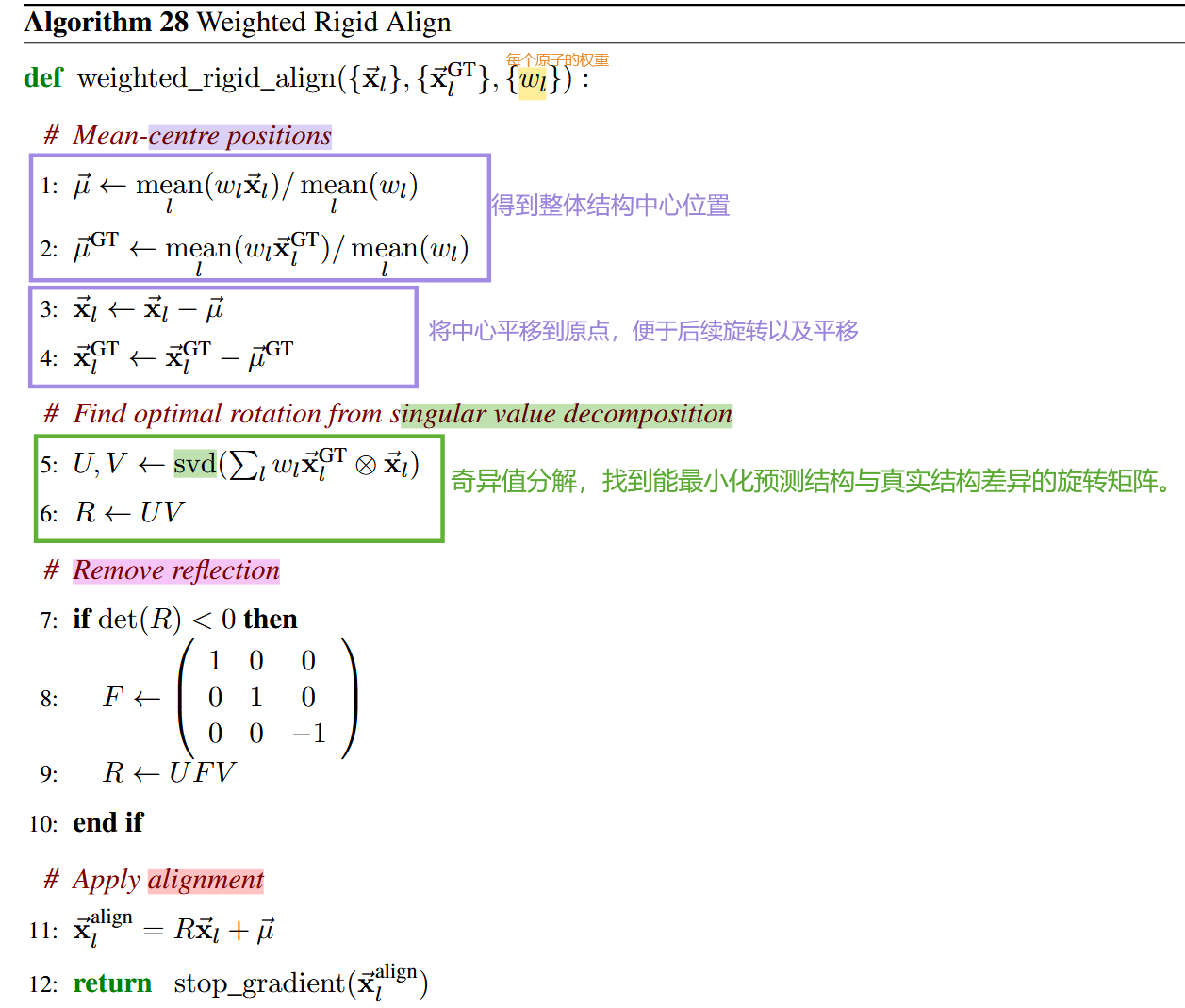
算法 28（weighted_rigid_align）用于对预测结构和真实结构进行加权刚性对齐，其核心目的是通过旋转和平移，消除预测结构与真实结构之间的全局姿态差异，使得后续计算损失时能更准确地衡量两者之间的位置差异。

在这里插入图片描述

步骤1-2：计算加权均值。分别计算预测结构和真实结构中原子坐标的加权平均值，得到质心 $μ⃗\vec{\mu}$ 和 $μ⃗GT\vec{\mu}^{\mathrm{GT}}$ 。这里使用加权均值是因为不同原子（如核酸、配体原子）在计算损失时权重不同，通过加权能更合理地反映整体结构的中心位置。
步骤3-4：对原子坐标进行中心化操作。将预测结构和真实结构中的每个原子坐标分别减去各自的质心，这样可以将结构的中心平移到原点，便于后续计算旋转矩阵，消除结构之间的平移差异。
步骤5：使用奇异值分解（SVD）计算旋转矩阵。对加权后的原子坐标外积和（ $∑lwlx⃗lGT⊗x⃗l\sum_lw_l\vec{\mathbf{x}}_l^\mathrm{GT}\otimes\vec{\mathbf{x}}_l$ ）进行奇异值分解，得到两个正交矩阵 U 和 V 。SVD 是一种在矩阵分解中常用的方法，能够将一个矩阵分解为多个矩阵的乘积形式，在这里用于找到能最小化预测结构与真实结构差异的旋转矩阵。
步骤6：构建旋转矩阵 R 。通过 U 和 V 计算得到旋转矩阵 R ，这个矩阵将用于对预测结构进行旋转，使其尽可能与真实结构对齐。
步骤7-10：消除反射情况。行列式 $det⁡(R)\det(R)$ 用于判断旋转矩阵是否包含反射变换（刚性变换只包括旋转和平移，不包括反射）。如果 $det⁡(R)<0\det(R) < 0$ ，说明旋转矩阵中存在反射成分，通过构建矩阵 F ，对旋转矩阵 R 进行修正，确保得到的旋转矩阵是一个 proper rotation（行列式为1的旋转矩阵），符合刚性变换的要求。
步骤11：应用对齐操作

Tero Karras, Miika Aittala, Timo Aila, and Samuli Laine. Elucidating the Design Space of Diffusion-Based Generative Models. In S. Koyejo, S. Mohamed, A. Agarwal, D. Belgrave, K. Cho, and A. Oh, editors, Advances in Neural Information Processing Systems, volume 35, pages 26565–26577. Curran Associates, Inc., 2022. ↩︎

查看全文

http://www.xdnf.cn/news/16570.html