当前位置： 首页 > ai >正文

二叉树的学习

ai 2025/8/2 2:12:58

二叉树

文章目录

  • 二叉树
  • 树型结构
    • 概念
    • 概念（重要）
    • 树的表现形式（了解）
    • 树的应用
  • 二叉树
    • 概念
    • 两种特殊的二叉树
    • 二叉树的性质
    • 二叉树的存储
    • 二叉树的基本操作

树型结构

概念

树形结构是一种重要的非线性数据结构，它由节点（元素）和节点之间的关联关系（边）组成，整体呈现“分支”和“层次”特性，类似自然界中的树。其核心特点是存在一个唯一的根节点，其余节点分为若干个互不相交的子集（子树），每个子集仍是树形结构。

概念（重要）

在这里插入图片描述

  1. 核心概念
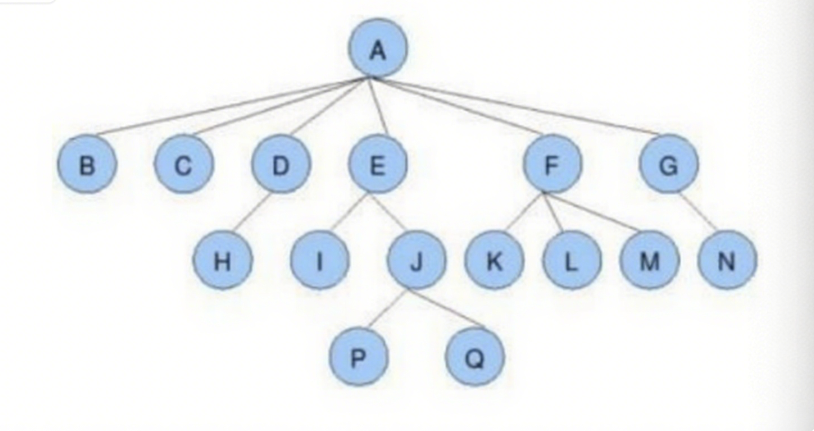
  • 节点的度：一个节点含有的子树的个数称为该节点的度。例如图中节点A的度为6。
  • 树的度：一棵树中，所有节点的度的最大值称为树的度。例如图中树的度为6。
  • 叶子结点（终端结点）：度为0的结点称为叶结点。例如图中B、C、H、L等节点为叶结点。
  • 双亲结点（父结点）：若一个结点含有子结点，则这个结点为其子结点的父结点。例如图中A是B的父结点。
  • 孩子结点（子结点）：一个结点含有的子树的根结点称为该结点的子结点。例如图中B是A的子结点。
  • 根结点：一棵树中，没有双亲结点的结点。例如图中A是根结点。
  • 结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推。
  1. 其他概念
  • 树的高度（深度）：树中结点的最大层次。例如图中树的高度为4。
  • 非终端结点（分支结点）：度不为0的结点。例如图中D、E、F、G等节点为分支结点。
  • 兄弟结点：具有相同父结点的结点互称为兄弟结点。例如图中B、C是兄弟结点。
  • 堂兄弟结点：双亲在同一层的结点互为堂兄弟。例如图中H、I为堂兄弟结点。
  • 结点的祖先：从根到该结点所经分支上的所有结点。例如图中A是所有结点的祖先。
  • 子孙：以某结点为根的子树中任一结点都称为该结点的子孙。例如图中所有结点都是A的子孙。
  • 森林：由m（m≥0）棵互不相交的树的集合称为森林。

树的表现形式（了解）

表示形式核心思想 / 结构设计优势劣势适用场景示例（以树 A→(B,C)，B→D 为例）
双亲表示法用数组存储节点，每个节点含数据域和父节点索引（根节点父索引为 - 1）快速查找父节点，结构简单，空间开销小查找子节点需遍历整个结构，效率低需频繁查找父节点的场景（如并查集）数组：索引 0（A，-1）、1（B，0）、2（C，0）、3（D，1）
孩子表示法每个节点含数据域和子节点列表（链表或数组形式）快速查找子节点，适合多子节点场景查找父节点需遍历所有节点，效率低需频繁查找子节点的场景（如多叉树遍历）A 的子列表 =[B,C]，B 的子列表 =[D]，C 和 D 的子列表为空
双亲-孩子表示法每个节点同时记录父节点（索引 / 指针）和子节点列表兼顾父节点和子节点的快速查找空间开销较大，结构较复杂需双向频繁查找（父 / 子节点）的场景节点 A：数据 = A，父 =-1，子列表 =[B,C]；节点 B：数据 = B，父 = 0，子列表 =[D]
孩子兄弟表示法用二叉树结构表示，左指针指向第一个子节点，右指针指向右兄弟节点将树转化为二叉树，便于复用二叉树算法理解和转换需遵循 “左孩子右兄弟” 规则需利用二叉树操作处理树的场景（最常用）A 左→B，B 右→C，B 左→D；C、D 的左右指针均为空
广义表表示法用括号和逗号描述层次，根节点后接子节点组成的子表直观易懂，适合文本化描述和输入输出不适合直接用于编程存储和操作理论分析、结构可视化或数据输入输出A(B(D), C)

树的应用

树作为一种重要的非线性数据结构，凭借其层次化、分支化的特性，在计算机科学、信息技术及其他领域有着广泛的应用。以下从多个领域详细介绍树的典型应用：

一、数据存储与检索

  • 数据库索引：
    B树、B+树是数据库中常用的索引结构。它们通过平衡的多叉树结构，减少磁盘I/O操作，提高数据查询、插入和删除的效率。例如，MySQL的InnoDB存储引擎就使用B+树作为索引，将表中的数据按主键有序组织，便于快速定位记录。

  • 文件系统：
    操作系统的文件系统（如Windows的NTFS、Linux的Ext4）采用树结构组织文件和目录。根目录是树的根节点，子目录和文件是其子孙节点，通过这种层级结构，用户可以方便地管理和访问文件，如路径/home/user/doc.txt就清晰地体现了树的层次关系。

二、编程语言与编译原理

  • 抽象语法树（AST）：
    在编译过程中，编译器会将源代码转换为抽象语法树。AST以树的形式表示代码的语法结构，每个节点代表代码中的一个语法单元（如表达式、语句、函数等）。例如，表达式a + b * c的AST中，根节点是“+”，左子节点是a，右子节点是“”，而“”的子节点是b和c。编译器通过遍历AST进行语法分析、语义检查和代码生成。

  • 继承关系树：
    在面向对象编程中，类的继承关系可以用树（或森林）表示。例如，Java中所有类都默认继承自Object类，Object是根节点，其他类作为其子节点或更深层的节点，这种结构体现了类之间的层级和继承关系。

三、算法与问题求解

  • 二叉搜索树（BST）：
    一种特殊的二叉树，左子树的所有节点值小于根节点值，右子树的所有节点值大于根节点值。利用这一特性，可实现高效的查找、插入和删除操作（平均时间复杂度为O(log n)），常用于动态数据的检索，如通讯录的查找功能。

二叉树

概念

二叉树是一种重要的树形数据结构，其特点是每个节点最多有两个子节点，分别称为左子节点和右子节点。这种结构既保留了树的层级特性，又因严格的子节点数量限制，便于实现高效的遍历和操作算法。以下从核心定义、基本特性、分类及相关概念展开说明：

两种特殊的二叉树

1.满二叉树

  • 定义：深度为 h 的二叉树中，每一层都有最大节点数（即第 i 层有 2^(i-1) 个节点），总节点数为 2^h - 1。
    特点：所有叶子节点都在最后一层，且非叶子节点的度均为 2。

2.完全二叉树

  • 定义：深度为 h 的二叉树，前 h-1 层为满二叉树，第 h 层的节点从左到右依次排列（无空缺）。
    特点：叶子节点仅在最后两层；若某节点度为 1，则其必为左子节点；适合用数组存储（通过索引快速定位父 / 子节点：若节点索引为 i，则父节点为 (i-1)//2，左子节点为 2i+1，右子节点为 2i+2）。

二叉树的性质

性质1：节点与边的数量关系

  • 内容：对任何一棵非空二叉树，若其包含 n 个节点，则边的数量为 n-1。
  • 解释：二叉树属于树形结构，根节点没有父节点，其余每个节点都恰好有一条边连接到父节点，因此边数比节点数少1。

性质2：层级与最大节点数

  • 内容：
    1. 若规定根节点的层级为1，则二叉树第 i 层最多有 2^(i-1) 个节点（i ≥ 1）。
    2. 深度为 h 的二叉树最多有 2^h - 1 个节点（此时为满二叉树）。
  • 解释：
    • 第1层（根节点）最多1个节点（2^0 = 1）；第2层最多2个节点（2^1 = 2）；第3层最多4个节点（2^2 = 4），以此类推，每层节点数呈等比数列增长。
    • 满二叉树的总节点数是各层最大节点数之和，即 2^0 + 2^1 + … + 2^(h-1) = 2^h - 1（等比数列求和公式）。

性质3：叶子节点与度为2的节点的关系

  • 内容：对任何非空二叉树，若叶子节点数为 n₀，度为2的节点数为 n₂，则有 n₀ = n₂ + 1。
  • 推导：
    1. 设度为1的节点数为 n₁，则总节点数 n = n₀ + n₁ + n₂。
    2. 二叉树中，边数 = 总节点数 - 1（性质1），即边数 = n - 1 = n₀ + n₁ + n₂ - 1。
    3. 同时，边数由各节点的子节点数决定：度为1的节点贡献1条边，度为2的节点贡献2条边，叶子节点（度为0）贡献0条边，因此边数 = n₁ + 2n₂。
    4. 联立两式：n₀ + n₁ + n₂ - 1 = n₁ + 2n₂，化简得 n₀ = n₂ + 1。

性质4：完全二叉树的节点索引特性

  • 内容：若完全二叉树按层序遍历（从根节点开始，每层从左到右）的顺序用数组存储（索引从0开始），则对任意节点 i（i ≥ 0）：
    • 左子节点的索引为 2i + 1（若存在）；
    • 右子节点的索引为 2i + 2（若存在）；
    • 父节点的索引为 (i - 1) // 2（若 i > 0）。
  • 示例：
    若节点索引为2，则左子节点为 2×2+1=5，右子节点为 2×2+2=6，父节点为 (2-1)//2=0。
  • 意义：完全二叉树的数组存储方式无需额外指针，通过索引公式即可快速定位父子节点，节省空间且操作高效。

性质5：完全二叉树的节点数与深度关系

  • 内容：具有 n 个节点的完全二叉树，其深度 h 为 floor(log₂n) + 1（floor(x) 表示向下取整）。
  • 解释：
    • 深度为 h-1 的满二叉树最多有 2^(h-1) - 1 个节点；
    • 深度为 h 的满二叉树最多有 2^h - 1 个节点；
    • 完全二叉树的节点数 n 满足 2^(h-1) ≤ n ≤ 2^h - 1，因此 h = floor(log₂n) + 1。

二叉树的存储

二叉树的存储方式主要有两种：顺序存储和链式存储，选择哪种方式取决于二叉树的类型和实际应用场景。以下是两种存储方式的详细说明：

一、顺序存储（数组存储）
顺序存储通过数组来存储二叉树的节点，利用节点在数组中的索引位置反映其在二叉树中的父子关系。

核心思想：

  • 适用于完全二叉树（或满二叉树），可高效利用存储空间；
  • 按层序遍历的顺序将节点存入数组（根节点在索引0，依次按层级从左到右存储）；
  • 通过索引公式快速定位父子节点（基于完全二叉树的性质4）：
    • 若节点索引为 i，则：
      • 左子节点索引 = 2i + 1（若存在）
      • 右子节点索引 = 2i + 2（若存在）
      • 父节点索引 = (i - 1) // 2（若 i > 0）

示例：
对于完全二叉树：

      1/   \2     3/ \   /4   5 6

数组存储形式为：[1, 2, 3, 4, 5, 6]

二、链式存储（链表存储）
链式存储通过指针（或引用） 连接节点，每个节点记录自身数据及子节点的地址，适用于各种类型的二叉树。

核心结构：
每个节点包含三部分信息（二叉链表）：

  • 数据域（data）：存储节点的值；
  • 左指针（left）：指向左子节点；
  • 右指针（right）：指向右子节点。

示例：
对于二叉树：

      A/   \B     C\D

链式存储结构为：

  • A.left = B，A.right = C
  • B.left = None，B.right = D
  • C.left = None，C.right = None
  • D.left = None，D.right = None

三、存储方式的选择

场景推荐存储方式原因分析
完全二叉树/满二叉树顺序存储（数组）空间利用率最高，父子节点定位高效
非完全二叉树（如斜树）链式存储（链表）避免顺序存储的空间浪费
需频繁插入/删除节点链式存储操作灵活，无需大量移动元素
需频繁查找父节点三叉链表直接通过父指针定位，无需遍历
内存受限，追求空间效率顺序存储（适用于完全二叉树）无指针开销，存储密度高

二叉树的基本操作

二叉树的基本操作包括创建、遍历、插入、删除、查找等，这些操作是实现二叉树相关算法的基础。以下是基于二叉链表存储结构的常用操作及实现思路（以Java为例）：

一、二叉树节点定义
首先定义二叉树的节点结构（二叉链表）：

class TreeNode {int val;                // 节点值TreeNode left;          // 左子节点TreeNode right;         // 右子节点// 构造方法public TreeNode(int val) {this.val = val;this.left = null;this.right = null;}
}

二、创建二叉树
手动构建一棵简单的二叉树（示例）：

public class BinaryTree {// 构建示例二叉树：//       1//      / \//     2   3//    / \//   4   5public static TreeNode createTree() {TreeNode root = new TreeNode(1);root.left = new TreeNode(2);root.right = new TreeNode(3);root.left.left = new TreeNode(4);root.left.right = new TreeNode(5);return root;}
}

三、遍历操作（核心）
遍历是按一定规则访问二叉树中所有节点，常见方式有4种：

  1. 前序遍历（根 → 左 → 右）
// 递归实现
public static void preOrder(TreeNode node) {if (node == null) return;System.out.print(node.val + " ");  // 访问根节点preOrder(node.left);               // 遍历左子树preOrder(node.right);              // 遍历右子树
}// 非递归实现（用栈）
public static void preOrderIterative(TreeNode root) {if (root == null) return;Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();System.out.print(node.val + " ");// 先压右子树，再压左子树（栈是先进后出）if (node.right != null) stack.push(node.right);if (node.left != null) stack.push(node.left);}
}
  1. 中序遍历（左 → 根 → 右）
// 递归实现
public static void inOrder(TreeNode node) {if (node == null) return;inOrder(node.left);                // 遍历左子树System.out.print(node.val + " ");  // 访问根节点inOrder(node.right);               // 遍历右子树
}// 非递归实现（用栈）
public static void inOrderIterative(TreeNode root) {if (root == null) return;Stack<TreeNode> stack = new Stack<>();TreeNode curr = root;while (curr != null || !stack.isEmpty()) {// 先遍历到最左节点while (curr != null) {stack.push(curr);curr = curr.left;}curr = stack.pop();System.out.print(curr.val + " ");curr = curr.right;  // 转向右子树}
}
  1. 后序遍历（左 → 右 → 根）
// 递归实现
public static void postOrder(TreeNode node) {if (node == null) return;postOrder(node.left);              // 遍历左子树postOrder(node.right);             // 遍历右子树System.out.print(node.val + " ");  // 访问根节点
}// 非递归实现（用栈，记录访问标记）
public static void postOrderIterative(TreeNode root) {if (root == null) return;Stack<TreeNode> stack = new Stack<>();TreeNode prev = null;stack.push(root);while (!stack.isEmpty()) {TreeNode curr = stack.peek();// 若当前节点无左右子树，或子树已访问，则访问当前节点if ((curr.left == null && curr.right == null) || (prev != null && (prev == curr.left || prev == curr.right))) {System.out.print(curr.val + " ");stack.pop();prev = curr;} else {// 先压右子树，再压左子树if (curr.right != null) stack.push(curr.right);if (curr.left != null) stack.push(curr.left);}}
}
  1. 层序遍历（按层级从左到右）
public static void levelOrder(TreeNode root) {if (root == null) return;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode node = queue.poll();System.out.print(node.val + " ");// 左子节点入队if (node.left != null) queue.offer(node.left);// 右子节点入队if (node.right != null) queue.offer(node.right);}
}

四、插入节点
在二叉树中插入节点需指定插入位置（左子树或右子树），以向指定节点的左/右插入为例：

// 向parent节点的左子树插入新节点（若左子树为空）
public static void insertLeft(TreeNode parent, int val) {if (parent == null) return;if (parent.left == null) {parent.left = new TreeNode(val);} else {// 若左子树不为空，可根据需求处理（如替换或插入到更深层）System.out.println("左子树已存在，插入失败");}
}// 向parent节点的右子树插入新节点（若右子树为空）
public static void insertRight(TreeNode parent, int val) {if (parent == null) return;if (parent.right == null) {parent.right = new TreeNode(val);} else {System.out.println("右子树已存在，插入失败");}
}

五、删除节点
删除节点是较复杂的操作，需根据节点的子树情况处理：

  1. 若节点为叶子节点（无左右子树）：直接删除（置为null）。
  2. 若节点有一个子树：用子树替代该节点。
  3. 若节点有两个子树：用右子树的最小节点（或左子树的最大节点）替代，再删除该最小节点。
public static TreeNode deleteNode(TreeNode root, int val) {if (root == null) return null;// 查找目标节点if (val < root.val) {root.left = deleteNode(root.left, val); // 去左子树删除} else if (val > root.val) {root.right = deleteNode(root.right, val); // 去右子树删除} else {// 找到目标节点，处理删除if (root.left == null) return root.right; // 左子树为空，返回右子树if (root.right == null) return root.left; // 右子树为空，返回左子树// 有两个子树：找右子树的最小节点（或左子树最大节点）TreeNode minNode = findMin(root.right);root.val = minNode.val; // 替换值root.right = deleteNode(root.right, minNode.val); // 删除最小节点}return root;
}// 查找以node为根的树的最小节点（最左节点）
private static TreeNode findMin(TreeNode node) {while (node.left != null) {node = node.left;}return node;
}

六、查找节点
查找指定值的节点（递归/非递归）：

// 递归查找
public static TreeNode findNode(TreeNode node, int val) {if (node == null) return null;if (node.val == val) return node;// 先在左子树查找，找不到再在右子树查找TreeNode leftResult = findNode(node.left, val);return leftResult != null ? leftResult : findNode(node.right, val);
}// 非递归查找（层序遍历）
public static TreeNode findNodeIterative(TreeNode root, int val) {if (root == null) return null;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode node = queue.poll();if (node.val == val) return node;if (node.left != null) queue.offer(node.left);if (node.right != null) queue.offer(node.right);}return null; // 未找到
}

七、其他常用操作

  1. 计算树的深度：
public static int getDepth(TreeNode node) {if (node == null) return 0;int leftDepth = getDepth(node.left);int rightDepth = getDepth(node.right);return Math.max(leftDepth, rightDepth) + 1;
}
  1. 计算节点总数：
public static int getNodeCount(TreeNode node) {if (node == null) return 0;return 1 + getNodeCount(node.left) + getNodeCount(node.right);
}
  1. 计算叶子节点数：
public static int getLeafCount(TreeNode node) {if (node == null) return 0;if (node.left == null && node.right == null) return 1; // 叶子节点return getLeafCount(node.left) + getLeafCount(node.right);
}

总结
二叉树的基本操作中，遍历是核心，其他操作（插入、删除、查找等）往往依赖遍历实现。递归是实现二叉树操作的简洁方式，但非递归方式（用栈或队列）在避免栈溢出方面更优。实际应用中，需根据二叉树的类型（如二叉搜索树、平衡树）选择合适的操作逻辑，以提高效率。

http://www.xdnf.cn/news/16551.html

相关文章：

  • 【Java】批量生成Excel放入文件夹并打zip压缩包
  • 八种AI记忆术，重构智能体的“大脑”
  • RFID 系统行业前沿洞察：技术跃迁与生态重构
  • 线性代数常见的解题方法
  • aws(学习笔记第五十课) ECS集中练习(2)
  • 【MySQL 数据库】MySQL索引特性（二）页目录（B和B+树）（非）聚簇索引 索引操作
  • APM32芯得 EP.27 | 告别IDE，为APM32F411打造轻量级命令行开发工作流
  • 《Computational principles and challenges in single-cell data integration》
  • Vite 模块动态导入之Glob导入
  • 微算法科技MLGO突破性的监督量子分类器：纠缠辅助训练算法为量子机器学习开辟新天地
  • PCB学习笔记（一）
  • LeetCode 面试经典 150_数组/字符串_轮转数组（6_189_C++_中等）（额外数组；转置）
  • dify + mcp 实现图片 ocr 识别
  • 实例教学FPN原理与PANet，Pytorch逐行精讲实现
  • [leetcode] Z字型变换
  • dify离线插件打包步骤
  • 手撕设计模式——智能家居之外观模式
  • C++线程详解
  • C++11 std::function 详解：通用多态函数包装器
  • 从0开始学习R语言--Day62--RE插补
  • 【ssh】ubuntu服务器+本地windows主机，使用密钥对进行ssh链接
  • Linux常用基础命令
  • 反射核心：invoke与setAccessible方法详解
  • Git 从入门到精通
  • linux命令ps的实际应用
  • SQL注入SQLi-LABS 靶场less26-30详细通关攻略
  • 深入解析Java元注解与运行时处理
  • ​第七篇：Python数据库编程与ORM实践
  • 前缀和-974.和可被k整除的子数组-力扣(LeetCode)
  • [mcp: JSON-RPC 2.0 规范]