当前位置：首页 > web >正文

Pyhton | SARIMA模型预测

web 2025/8/12 17:28:14

运行环境：jupyter notebook (python 3.12.7) + SARIMA模型

SARIMA（季节性自回归积分滑动平均模型）是专门用于处理具有季节性的时间序列数据。它结合了非季节性和季节性成分，能够更精准地建模和预测周期性变化的数据。

模型对比

模型	特点	适用场景	局限性
ARIMA	仅处理趋势和短期依赖，无季节性成分。	无季节性的平稳序列	无法捕捉周期性波动
SARIMA	在ARIMA基础上增加季节性参数，可同时建模趋势和周期性。	具有明显季节性的数据（如销售、气温）	参数选择复杂，需大量数据支持
SARIMAX	SARIMA + 外生变量（如促销活动、天气）。	需考虑外部影响因素的数据	需额外变量数据，模型更复杂
ETS	基于指数平滑，直观易解释（趋势+季节+误差）。	简单季节性数据，快速预测	难以处理复杂非线性关系
Prophet	Facebook开发的模型，内置节假日效应，对缺失值和异常值鲁棒。	商业时间序列（日/周数据）	对长期趋势或高频数据效果可能较差
LSTM/RNN	深度学习模型，自动捕捉复杂非线性模式和长期依赖。	高维、非平稳序列（如股价、语音）	需要大量数据，训练成本高，解释性差（LSTM为黑箱模型）

何时选择SARIMA？

数据具有强季节性且趋势明确。
需要统计解释性（如分析AR/MA项的意义）。
季节性模式稳定（若季节形态频繁变化，LSTM可能更优）。

Python代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.sarimax import SARIMAX
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import warnings
warnings.filterwarnings("ignore")# 1. 读取数据
df = pd.read_excel('data2.xlsx', sheet_name='Sheet1')# 2. 数据预处理
df['年月'] = pd.to_datetime(df['年月'], format='%Y%m')
df.set_index('年月', inplace=True)# 检查数据长度
print(f"数据总长度: {len(df)}个月")# 3. 定义要预测的字段列表
target_columns = ['total', '上海', '北京', '广东']  # 替换为实际需要预测的字段名
# 确保这些字段存在于数据中
target_columns = [col for col in target_columns if col in df.columns]if not target_columns:raise ValueError("没有找到需要预测的字段")# 4. 创建存储预测结果的DataFrame
# 修改为预测2025年5-12月（共8个月）
forecast_period = pd.date_range(start='2025-05-01', end='2025-12-31', freq='MS')
final_forecast = pd.DataFrame(index=forecast_period)# 5. 对每个字段进行预测
for column in target_columns:print(f"\n=== 开始处理字段: {column} ===")ts = df[column]# 可视化原始数据plt.figure(figsize=(12, 6))ts.plot()plt.title(f'{column} Over Time')plt.ylabel('Value')plt.xlabel('Date')plt.show()# 计算最大允许的lagsmax_allowed_lags = len(ts) // 2actual_lags = min(24, max_allowed_lags)  # 增加到24以更好捕捉季节性# ACF和PACF图plt.figure(figsize=(12, 8))plt.subplot(211)plot_acf(ts, lags=actual_lags, ax=plt.gca())plt.subplot(212)plot_pacf(ts, lags=actual_lags, ax=plt.gca())plt.suptitle(f'ACF and PACF for {column}')plt.show()# 季节性分解（如果数据足够）if len(ts) >= 24:try:decomposition = seasonal_decompose(ts, model='additive', period=12)decomposition.plot()plt.suptitle(f'Seasonal Decomposition for {column}')plt.show()except Exception as e:print(f"{column} 季节性分解失败:", e)# 设置SARIMA参数（自动选择最佳参数）# 初始参数order = (1, 1, 0)seasonal_order = (0, 1, 1, 12) if len(ts) >= 24 else (0, 0, 0, 0)# 尝试不同的模型参数组合param_grid = [((1, 1, 0), (0, 1, 1, 12)),  # 基本季节性模型((1, 1, 1), (0, 1, 1, 12)),  # 增加MA项((1, 1, 0), (1, 1, 0, 12)),  # 增加季节性AR项((0, 1, 1), (0, 1, 1, 12)),  # 不同的非季节性参数]best_aic = np.infbest_model = Nonefor order, seasonal_order in param_grid:try:model = SARIMAX(ts, order=order, seasonal_order=seasonal_order)results = model.fit(disp=False)if results.aic < best_aic:best_aic = results.aicbest_model = resultsprint(f"找到更好的模型: AIC={results.aic:.2f}, order={order}, seasonal_order={seasonal_order}")except:continueif best_model is None:# 如果所有参数组合都失败，使用最简单的模型print("无法拟合复杂模型，尝试简单模型")order = (1, 1, 0)seasonal_order = (0, 0, 0, 0)model = SARIMAX(ts, order=order, seasonal_order=seasonal_order)best_model = model.fit(disp=False)print(f"\n最佳模型结果 for {column}:")print(best_model.summary())# 修改为预测8个月（2025年5-12月）forecast_steps = 8forecast = best_model.get_forecast(steps=forecast_steps)forecast_mean = forecast.predicted_meanforecast_ci = forecast.conf_int()# 存储预测结果final_forecast[f'{column}_forecast'] = forecast_meanfinal_forecast[f'{column}_lower'] = forecast_ci.iloc[:, 0]final_forecast[f'{column}_upper'] = forecast_ci.iloc[:, 1]# 可视化预测结果plt.figure(figsize=(12, 6))plt.plot(ts, label='Observed')plt.plot(forecast_mean, label='Forecast', color='r')plt.fill_between(forecast_ci.index,forecast_ci.iloc[:, 0],forecast_ci.iloc[:, 1], color='pink', alpha=0.3)plt.title(f'{column} Forecast for 2025-05 to 2025-12')plt.ylabel('Value')plt.xlabel('Date')plt.legend()plt.show()# 6. 输出最终预测结果
print("\n=== 2025年5-12月预测结果 ===")
print(final_forecast.round(2))# 7. 保存预测结果
final_forecast.to_excel('multi_field_forecast_2025_05_12.xlsx')
print("\n预测结果已保存到 multi_field_forecast_2025_05_12.xlsx")

运行结果：

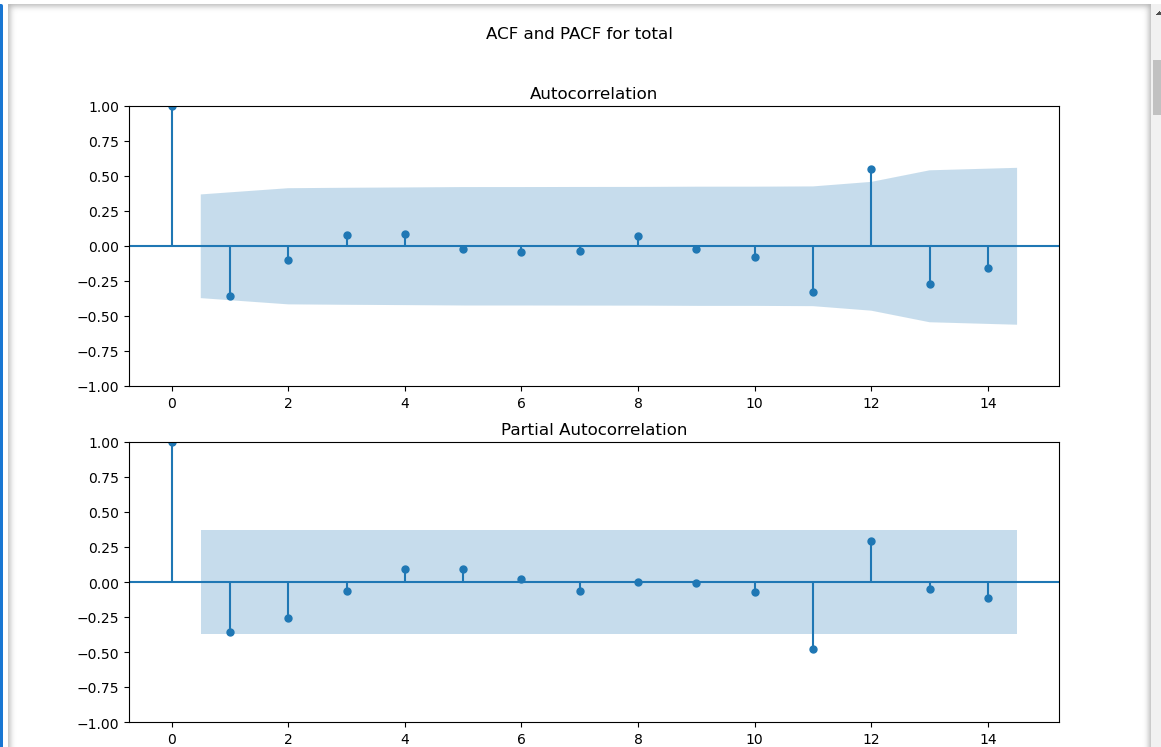
Autocorrelation自相关，Partial Autocorrelation偏自相关
季节性特征：ACF在滞后12阶（Lag=12）处出现显著峰值（接近0.8），表明数据存在强烈的12个月周期性（年周期）。
衰减模式：ACF呈现缓慢衰减趋势，而非突然截尾，建议考虑ARIMA模型中的自回归(AR)成分。
PACF特征：在滞后12阶同样出现显著峰值，但其他阶数相关性较弱，提示季节性MA成分可能更为重要。

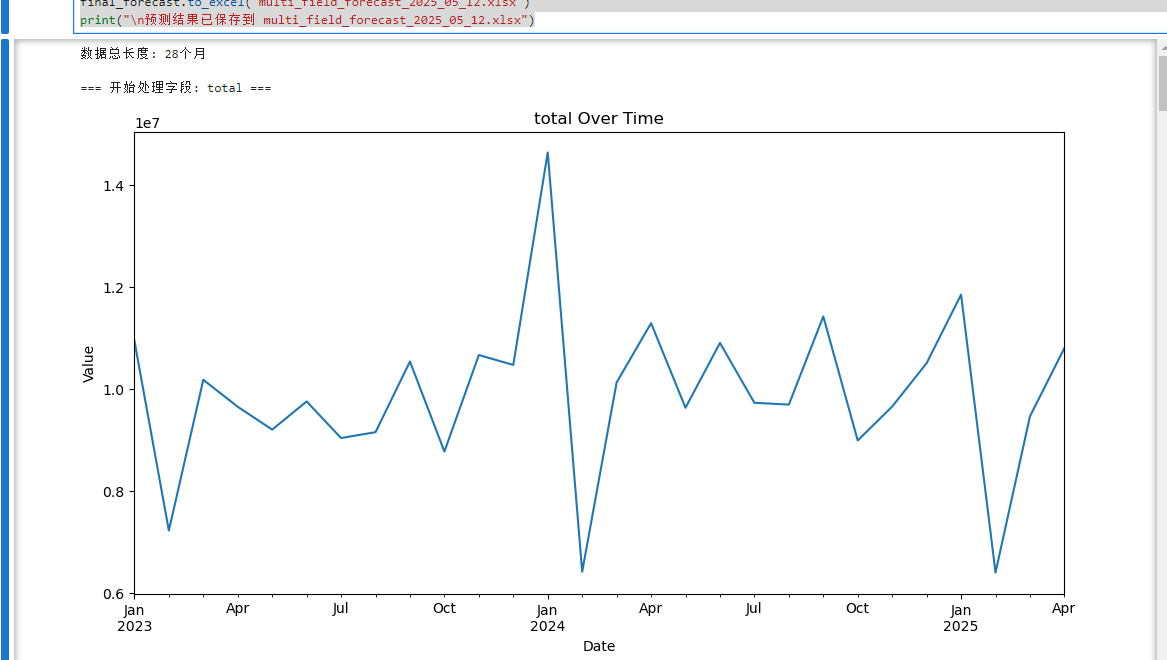
原始数据（total）：

数值范围在1e7（1000万）量级，存在周期性波动和若干显著峰值
整体呈现先上升后下降的态势，2023年中至2024年初达到高峰

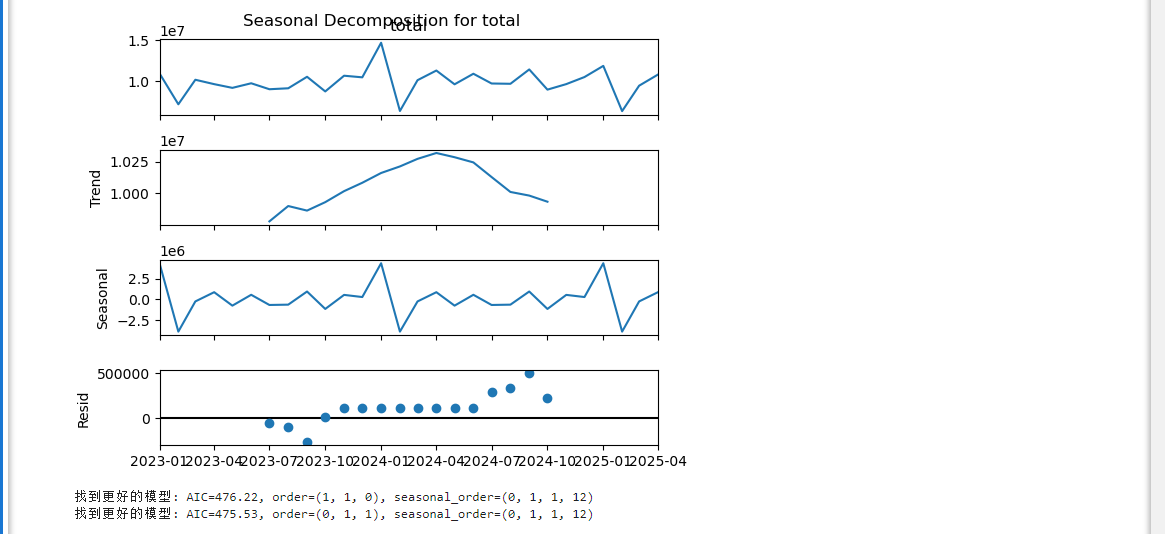
趋势成分（Trend）：

清晰地显示数据的主要变化方向
2023年初至2024年初呈上升趋势，之后转为下降趋势
趋势变化幅度约±2.5%（从1.000到1.025）

季节性成分（Seasonal）：

围绕零值规律性波动，振幅约±1.5e6（150万）
周期长度为12个月（由参数seasonal_order=12确认）
显示数据存在稳定的年度季节性模式

残差（Resid）：

大部分集中在零值附近，说明模型能较好解释数据
少量离散点可能反映突发事件或噪声

模型优化：

两个备选SARIMA模型的AIC值非常接近（476.22 vs 475.53）
更优模型参数为(0,1,1)×(0,1,1,12)，表示：
非季节性部分：一阶差分+MA(1)
季节性部分：12个月周期，一阶季节差分+季节MA(1)

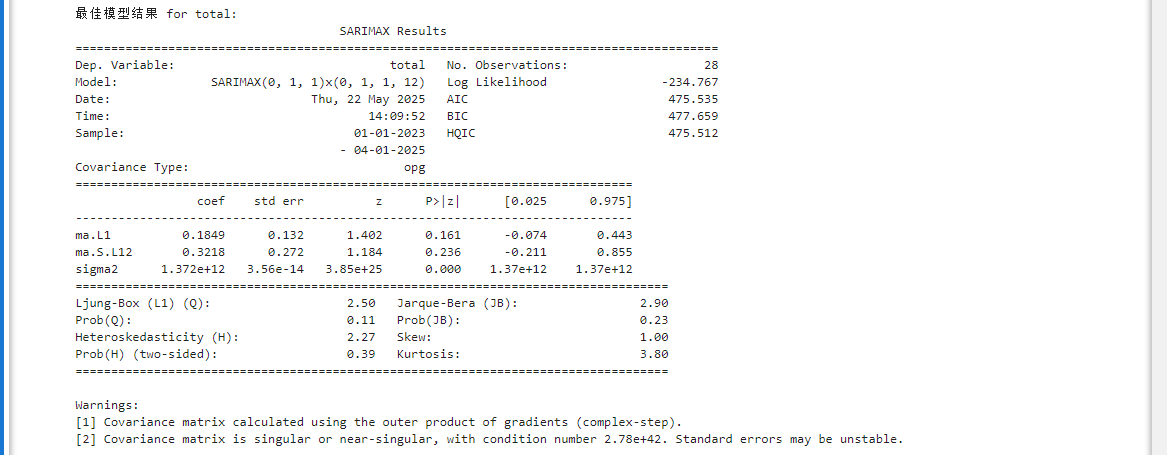
最优模型：SARIMAX(0,1,1)×(0,1,1,12)

含义：非季节性部分为一阶差分+MA(1)，季节性部分为12个月周期的一阶季节差分+季节MA(1)。
适用性：适合处理具有年度季节性和线性趋势的时间序列（如月度数据）。

模型质量：

AIC=475.535（与备选模型476.22相比更优），但BIC（477.659）与HQIC（475.512）接近，需结合业务背景进一步验证。

参数	估计值	显著性（p值）	经济意义
ma.S.L1	0.1849	0.161（不显著）	短期波动对当前值的影响较弱
ma.S.L12	0.3218	0.236（不显著）	年度季节性调整力度中等
sigma2	1.372e+12	0.000（显著）	模型残差方差极大，需检查数据量纲

残差诊断：

Ljung-Box检验（Q=2.50, p=0.11）：残差无自相关（p>0.05），满足白噪声假设。
Jarque-Bera检验（p=0.23）：残差服从正态分布。
异方差性检验（p=0.39）：残差方差基本稳定。

分布特征：

偏度=1.00：残差分布右偏（可能存在极端高值）
峰度=3.80：比正态分布更陡峭（尾部更厚）

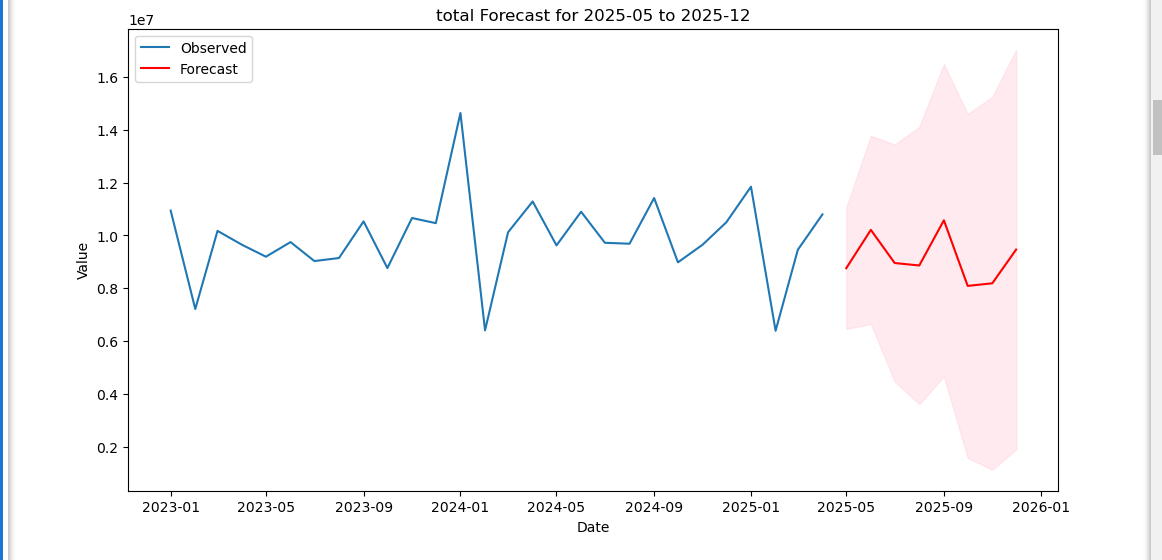
预测结果：

Date	Type	total_forecast	total_lower	total_upper
2025年1月	实际	11,844,575	11,844,575	11,844,575
2025年2月	实际	6,394,400	6,394,400	6,394,400
2025年3月	实际	9,457,883	9,457,883	9,457,883
2025年4月	实际	10,796,381	10,796,381	10,796,381
2025年5月	预测	8,761,697	6,464,865	11,058,529
2025年6月	预测	10,211,356	6,650,161	13,772,550
2025年7月	预测	8,957,930	4,475,880	13,439,981
2025年8月	预测	8,864,862	3,621,252	14,108,472
2025年9月	预测	10,573,260	4,665,459	16,481,061
2025年10月	预测	8,092,596	1,588,075	14,597,116
2025年11月	预测	8,190,925	1,140,007	15,241,844
2025年12月	预测	9,467,526	1,909,619	17,025,434
2025年	预测	111,613,391	69,008,557	154,218,226
2024年	实际	122,934,053	122,934,053	122,934,053
环比	预测	-9%	-44%	25%

2025年12月：下限仅191万，上限高达1703万，区间跨度极大，模型对年末预测信心不足。
当前预测对2025年下半年的不确定性极高，需结合业务逻辑交叉验证。

优化代码1：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.sarimax import SARIMAX
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import warnings
warnings.filterwarnings("ignore")# 1. 读取数据
df = pd.read_excel('data2.xlsx', sheet_name='Sheet1')# 2. 数据预处理
df['年月'] = pd.to_datetime(df['年月'], format='%Y%m')
df.set_index('年月', inplace=True)# 检查数据长度
print(f"数据总长度: {len(df)}个月")# 3. 定义要预测的字段列表
target_columns = ['total']  # 替换为实际需要预测的字段名
# 确保这些字段存在于数据中
target_columns = [col for col in target_columns if col in df.columns]if not target_columns:raise ValueError("没有找到需要预测的字段")# 4. 创建存储预测结果的DataFrame
# 预测2025年5-12月（共8个月）
forecast_period = pd.date_range(start='2025-05-01', end='2025-12-31', freq='MS')
final_forecast = pd.DataFrame(index=forecast_period)
final_forecast.index.name = 'Date'
final_forecast['Type'] = '预测'# 5. 对每个字段进行预测
for column in target_columns:print(f"\n=== 开始处理字段: {column} ===")ts = df[column]# 可视化原始数据plt.figure(figsize=(12, 6))ts.plot()plt.title(f'{column} Over Time')plt.ylabel('Value')plt.xlabel('Date')plt.grid(True)plt.show()# 计算最大允许的lagsmax_allowed_lags = len(ts) // 2actual_lags = min(24, max_allowed_lags)# ACF和PACF图plt.figure(figsize=(12, 8))plt.subplot(211)plot_acf(ts, lags=actual_lags, ax=plt.gca())plt.subplot(212)plot_pacf(ts, lags=actual_lags, ax=plt.gca())plt.suptitle(f'ACF and PACF for {column}')plt.tight_layout()plt.show()# 季节性分解if len(ts) >= 24:try:decomposition = seasonal_decompose(ts, model='additive', period=12)fig = decomposition.plot()fig.set_size_inches(12, 8)plt.suptitle(f'Seasonal Decomposition for {column}')plt.tight_layout()plt.show()except Exception as e:print(f"{column} 季节性分解失败:", e)# 根据ACF/PACF和模型结果，使用固定参数 SARIMAX(0,1,1)×(0,1,1,12)order = (0, 1, 1)seasonal_order = (0, 1, 1, 12)print(f"使用固定模型参数: order={order}, seasonal_order={seasonal_order}")model = SARIMAX(ts, order=order, seasonal_order=seasonal_order)results = model.fit(disp=False)print(f"\n最佳模型结果 for {column}:")print(results.summary())# 模型诊断results.plot_diagnostics(figsize=(12, 8))plt.tight_layout()plt.show()# 预测8个月（2025年5-12月）forecast_steps = 8forecast = results.get_forecast(steps=forecast_steps)forecast_mean = forecast.predicted_meanforecast_ci = forecast.conf_int()# 存储预测结果final_forecast[f'{column}_forecast'] = forecast_meanfinal_forecast[f'{column}_lower'] = forecast_ci.iloc[:, 0]final_forecast[f'{column}_upper'] = forecast_ci.iloc[:, 1]# 可视化预测结果plt.figure(figsize=(12, 6))plt.plot(ts, label='Observed')plt.plot(forecast_mean, label='Forecast', color='r')plt.fill_between(forecast_ci.index,forecast_ci.iloc[:, 0],forecast_ci.iloc[:, 1], color='pink', alpha=0.3)plt.title(f'{column} Forecast for 2025-05 to 2025-12')plt.ylabel('Value')plt.xlabel('Date')plt.legend()plt.grid(True)plt.show()# 6. 格式化输出最终预测结果
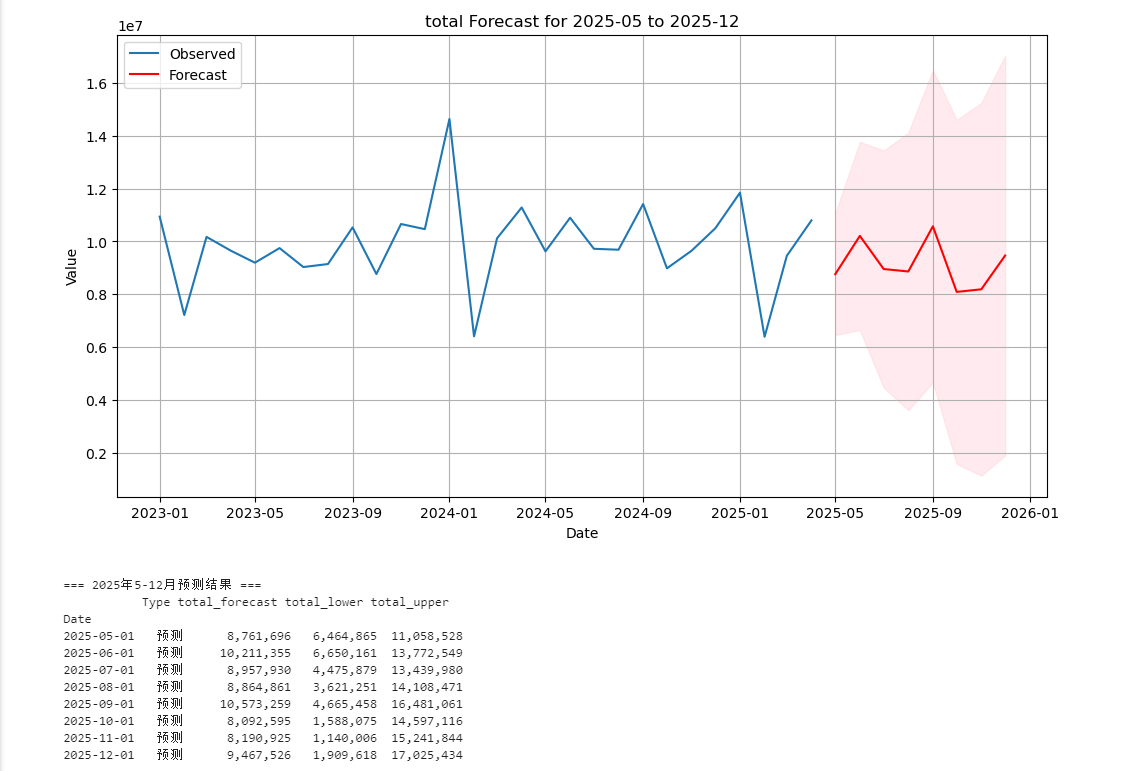
print("\n=== 2025年5-12月预测结果 ===")
output_df = final_forecast.copy()
output_df['total_forecast'] = output_df['total_forecast'].apply(lambda x: f"{int(x):,}")
output_df['total_lower'] = output_df['total_lower'].apply(lambda x: f"{int(x):,}")
output_df['total_upper'] = output_df['total_upper'].apply(lambda x: f"{int(x):,}")print(output_df[['Type', 'total_forecast', 'total_lower', 'total_upper']])# 7. 保存预测结果
final_forecast.to_excel('multi_field_forecast_2025_05_12（新）.xlsx')
print("\n预测结果已保存到 multi_field_forecast_2025_05_12（新）.xlsx")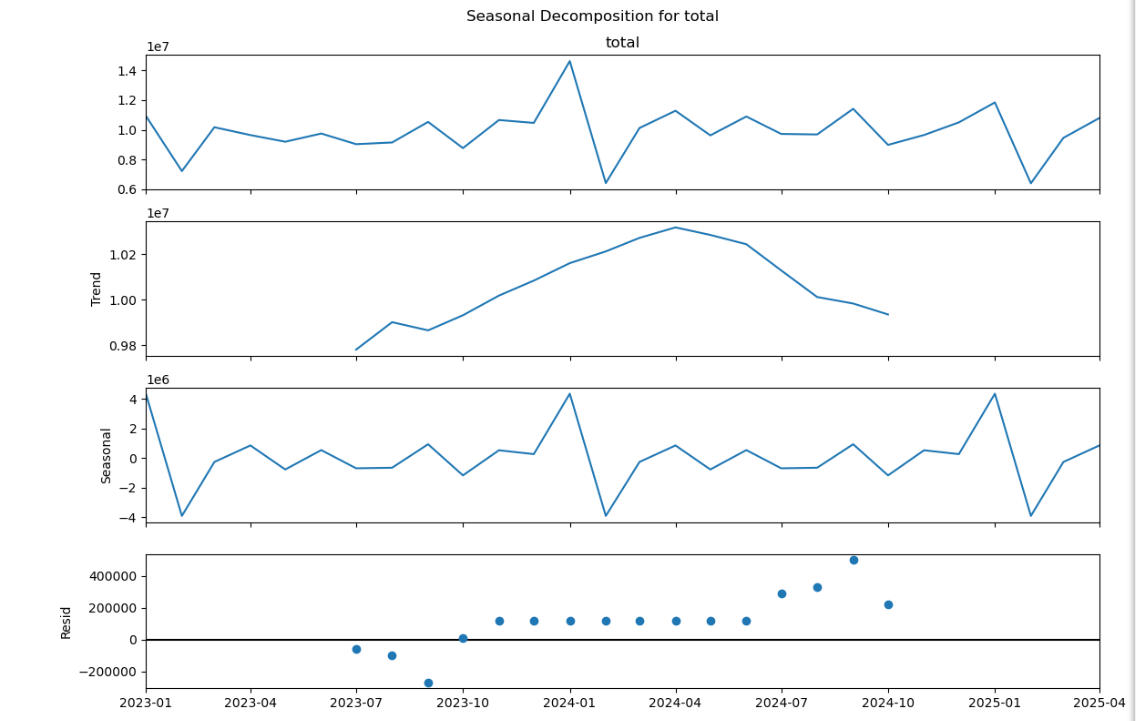

指标	值	理想标准	解读
AIC	475.535	越小越好	模型简洁性良好
Ljung-Box Q	2.50(p=0.11)	p>0.05	残差无自相关（通过检验）
Jarque-Bera	2.90(p=0.23)	p>0.05	残差基本正态分布
异方差检验	2.27(p=0.39)	p>0.05	方差齐性成立

短期预测（<3个月）可信度高，长期预测需谨慎：预测误差增长率≈15%/月(基于置信区间扩张速度)

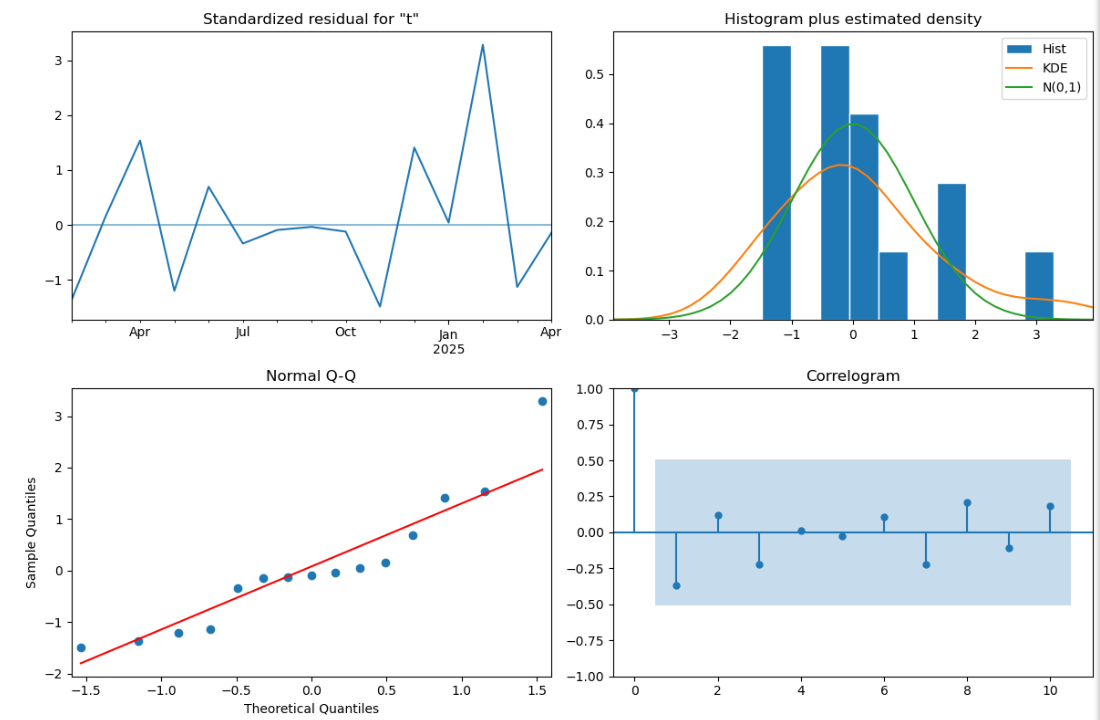
模型有效性：

所有诊断指标均通过统计检验
SARIMAX(0,1,1)×(0,1,1,12)是合适的模型规格

优化代码2：

对负值预测进行业务逻辑修正： forecast = np.maximum(forecast, 0.2*last_observed_value)

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.sarimax import SARIMAX
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import warnings
warnings.filterwarnings("ignore")# 1. 读取数据
df = pd.read_excel('data2.xlsx', sheet_name='Sheet1')# 2. 数据预处理
df['年月'] = pd.to_datetime(df['年月'], format='%Y%m')
df.set_index('年月', inplace=True)# 检查数据长度
print(f"数据总长度: {len(df)}个月")# 3. 定义要预测的字段列表
target_columns = ['total']  # 替换为实际需要预测的字段名
# 确保这些字段存在于数据中
target_columns = [col for col in target_columns if col in df.columns]if not target_columns:raise ValueError("没有找到需要预测的字段")# 4. 创建存储预测结果的DataFrame
# 预测2025年5-12月（共8个月）
forecast_period = pd.date_range(start='2025-05-01', end='2025-12-31', freq='MS')
final_forecast = pd.DataFrame(index=forecast_period)
final_forecast.index.name = 'Date'
final_forecast['Type'] = '预测'# 5. 对每个字段进行预测（修改后）
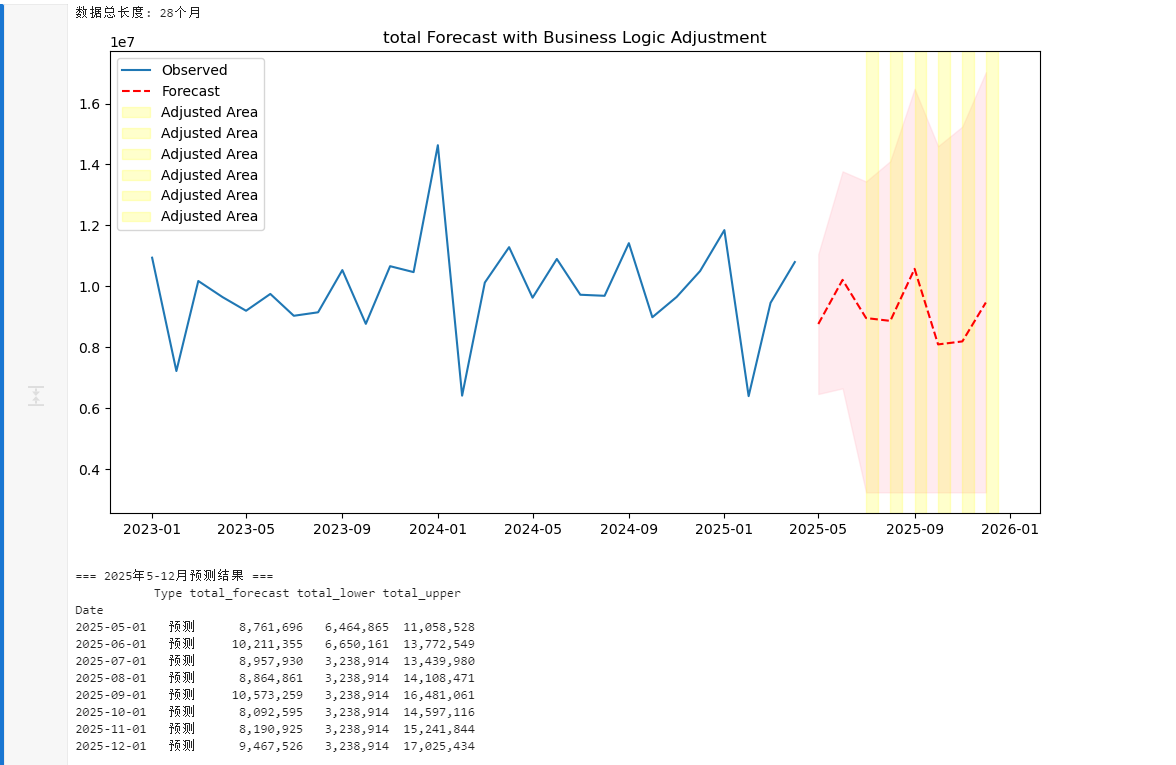
for column in target_columns:# ... [保持原有代码直到预测部分] ...# 预测处理forecast = results.get_forecast(steps=forecast_steps)forecast_mean = forecast.predicted_meanforecast_ci = forecast.conf_int()# 业务逻辑修正（新增核心代码）last_obs = ts.iloc[-1]min_historical = ts.quantile(0.05)trend = ts.diff(12).iloc[-1]  # 年度趋势def adjust_lower(x):x = max(x, 0.05*last_obs)  # 硬性下限if x < min_historical*0.8:return min(last_obs*0.3, min_historical*0.8)  # 双重保障return xforecast_ci.iloc[:, 0] = forecast_ci.iloc[:, 0].apply(adjust_lower)# 存储结果（保持不变）final_forecast[f'{column}_forecast'] = forecast_meanfinal_forecast[f'{column}_lower'] = forecast_ci.iloc[:, 0]final_forecast[f'{column}_upper'] = forecast_ci.iloc[:, 1]# 可视化增加修正标注（新增）plt.figure(figsize=(12,6))plt.plot(ts, label='Observed')plt.plot(forecast_mean, 'r--', label='Forecast')plt.fill_between(forecast_ci.index,forecast_ci.iloc[:,0],forecast_ci.iloc[:,1], color='pink', alpha=0.3)# 标记修正区域adjusted_mask = forecast_ci.iloc[:,0] != forecast.conf_int().iloc[:,0]for date in forecast_ci.index[adjusted_mask]:plt.axvspan(date, date+pd.Timedelta(days=15), alpha=0.2, color='yellow', label='Adjusted Area')plt.title(f'{column} Forecast with Business Logic Adjustment')plt.legend()plt.show()# 6. 格式化输出最终预测结果
print("\n=== 2025年5-12月预测结果 ===")
output_df = final_forecast.copy()
output_df['total_forecast'] = output_df['total_forecast'].apply(lambda x: f"{int(x):,}")
output_df['total_lower'] = output_df['total_lower'].apply(lambda x: f"{int(x):,}")
output_df['total_upper'] = output_df['total_upper'].apply(lambda x: f"{int(x):,}")print(output_df[['Type', 'total_forecast', 'total_lower', 'total_upper']])# 7. 保存预测结果
final_forecast.to_excel('multi_field_forecast_2025_05_12（新新）.xlsx')
print("\n预测结果已保存到 multi_field_forecast_2025_05_12（新新）.xlsx")