基于Cholesky分解求解逆矩阵
基于Cholesky分解求解逆矩阵
将对称正定矩阵分解为下三角矩阵与其转置矩阵的乘积
数值计算例子,MATLAB仿真
文章目录
- 前言
- 一、Cholesky分解简介
- 二、Cholesky分解
- 三、数值计算例子 实矩阵Cholesky分解
- 四、MATLAB仿真
- 1、实矩阵仿真
- 2、复矩阵仿真
- 五、求逆矩阵
- 总结
前言
\;\;\;\;\; 今天学习了Cholesky分解,学会了怎样用它将正定矩阵分解成2个三角矩阵的乘积。实矩阵和复矩阵均可以使用Cholesky分解。本文将介绍Cholesky分解相关的知识,同时也会通过列举数值例子说明如何将一个矩阵通过Cholesky分解为2个三角矩阵的乘积。最后,会用MATLAB进行仿真,验证Cholesky分解正确。
提示:文章系笔者原创,侵权必究!对您有用的话请一键三连支持一下!
一、Cholesky分解简介
\;\;\;\;\; Cholesky 分解是一种将对称正定矩阵分解为下三角矩阵与其转置矩阵乘积的矩阵分解方法。具体而言,对于给定的对称正定矩阵 A,存在一个下三角矩阵 L,使得 A = L L T A = LL^T A=LLT,其中 L T L^T LT 表示 L 的转置矩阵。这种分解在数值线性代数中具有重要应用,特别是在求解线性方程组和进行矩阵求逆等操作时,能够显著提高计算效率和数值稳定性。
Cholesky 分解适用条件
- 矩阵必须是(共轭)对称的
- 矩阵必须是正定的(矩阵所有特征值必须为正数)
- 矩阵必须是方阵
二、Cholesky分解
\;\;\;\;\; 对于一个对称正定实数/复数矩阵 A \mathbf{A} A, 使用Cholesky 分解可以将其分解为下三角矩阵与其(共轭)转置矩阵乘积,即
A = [ l 11 ⋮ ⋱ l k 1 ⋯ l k k ⋮ ⋮ ⋱ l N 1 ⋯ l N k ⋯ l N N ] . [ l 11 ∗ ⋯ l k 1 ∗ ⋯ l N 1 ∗ ⋱ ⋮ ⋮ l k k ∗ ⋯ l N k ∗ ⋱ ⋮ l N N ∗ ] = L L H \begin{aligned} \mathbf{A}=\begin{bmatrix} l_{11} \\ \vdots & \ddots \\ l_{k1} & \cdots & l_{kk} \\ \vdots & & \vdots & \ddots \\ l_{N1} & \cdots & l_{Nk} & \cdots & l_{NN} \end{bmatrix}. \begin{bmatrix} l_{11}^* & \cdots & l_{k1}^* & \cdots & l_{N1}^* \\ & \ddots & \vdots & & \vdots \\ & & l_{kk}^* & \cdots & l_{Nk}^* \\ & & & \ddots & \vdots \\ & & & & l_{NN}^* \end{bmatrix}= \mathbf{L}\mathbf{L}^{\mathrm{H}} \end{aligned} A= l11⋮lk1⋮lN1⋱⋯⋯lkk⋮lNk⋱⋯lNN . l11∗⋯⋱lk1∗⋮lkk∗⋯⋯⋱lN1∗⋮lNk∗⋮lNN∗ =LLH 对于实数矩阵,不用取共轭。
\;\;\;\;\; Cholesky 分解算法如下:
for p = 1,…,N
\;\;\;\;\; for q = 1,…,p-1
\;\;\;\;\; \;\;\;\;\; l p q = ( a p q − ∑ k = 1 q − 1 l p k l q k ∗ ) / l q q l_{pq}=\left(a_{pq}-\sum_{k=1}^{q-1}l_{pk}l_{qk}^*\right)/l_{qq} lpq=(apq−∑k=1q−1lpklqk∗)/lqq
\;\;\;\;\; end
\;\;\;\;\; l p p = a p p − ∑ k = 1 p − 1 l p k l p k ∗ l_{pp}=\sqrt{a_{pp}-\sum_{k=1}^{p-1}l_{pk}l_{pk}^*} lpp=app−∑k=1p−1lpklpk∗
end
显然,Cholesky 分解涉及到开方运算,如果是分解实数矩阵,则去掉公式中的共轭符号。Cholesky 分解的复杂度为 o ( n 3 / 3 ) o(n^3/3) o(n3/3)。
三、数值计算例子 实矩阵Cholesky分解
\;\;\;\;\; 已知对称正定矩阵 A = [ 4 6 8 6 13 14 8 14 26 ] A= \begin{bmatrix} 4 & 6 & 8 \\ 6 & 13 & 14 \\ 8 & 14 & 26 \end{bmatrix} A= 4686131481426 ,对其进行Cholesky分解。
l 11 = a 11 = 4 = 2 l_{11}=\sqrt{a_{11}}=\sqrt{4}=2 l11=a11=4=2 l 21 = a 21 / l 11 = 6 / 2 = 3 l_{21}=a_{21}/l_{11}=6/2=3 l21=a21/l11=6/2=3 l 22 = a 22 − l 21 l 21 = 13 − 3 ∗ 3 = 2 l_{22}=\sqrt{a_{22}-l_{21}l_{21}}=\sqrt{13-3*3}=2 l22=a22−l21l21=13−3∗3=2 l 31 = a 31 / l 11 = 8 / 2 = 4 l_{31}=a_{31}/l_{11}=8/2=4 l31=a31/l11=8/2=4 l 32 = ( a 32 − l 31 l 21 ) / l 22 = ( 14 − 4 ∗ 3 ) / 2 = 1 l_{32}=(a_{32}-l_{31}l_{21})/l_{22}=(14-4*3)/2=1 l32=(a32−l31l21)/l22=(14−4∗3)/2=1 l 33 = a 33 − l 31 l 31 − l 32 l 32 = 26 − 4 ∗ 4 − 1 ∗ 1 = 3 l_{33}=\sqrt{a_{33}-l_{31}l_{31}-l_{32}l_{32}}=\sqrt{26-4*4-1*1}=3 l33=a33−l31l31−l32l32=26−4∗4−1∗1=3
四、MATLAB仿真
1、实矩阵仿真

可见结果和上面数值计算的结果一模一样。
2、复矩阵仿真
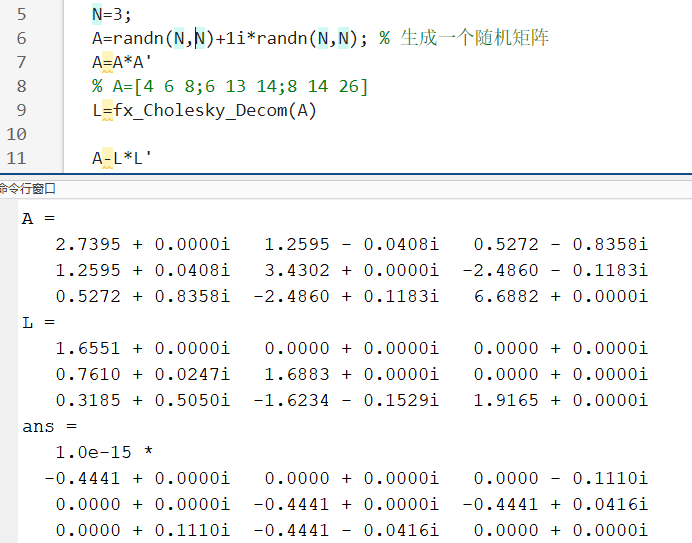
这里,注意到,分解后的L矩阵的主对角线元素全为正数,分解具有唯一性(唯一性的判断)。
五、求逆矩阵
分解得到 L \mathbf{L} L矩阵后可参考下面一篇文章求逆矩阵:
一种基于约化因子上三角矩阵求逆方法与MATLAB仿真
总结
\;\;\;\;\; 以上就是今天要讲的内容,本文介绍了Cholesky分解,说明了其适用条件,以及怎样用它将对称正定矩阵分解为下三角矩阵与其转置矩阵乘积。另外,还给了一个Cholesky分解的数值计算例子,同时,也用MATLAB验证了Cholesky分解的正确性。
