【沉浸式解决问题】浮点数计算精度误差，round后值错误，0.1+0.2不等于0.3？

一、问题描述

早就知道数据类型浮点数的精确度问题，但是一直没有实际遇到错误，没什么感觉，最近在生成小数后进行比较时发现本该相同的值却不相同，导致了判断错误，今天来深入研究一下。

---

二、场景还原

在python中存储一个统计字典时，key设计为从0到1分100个区间的中点，也就是0.005，0.015，0.025，0.035，，，0.985，0.995。
后面通过迭代统计列表生成统计字典

# 计算每个区间的中心位置
bin_centers = {round(i/100, 3) + 0.005: 0 for i in range(100)}
# 创建频数字典
data = {round(center, 3): int(count) for center, count in zip(bin_centers, counts)}

再生成一个总的统计字典

all_data = {round(i/100, 3) + 0.005: 0 for i in range(100)}

然后把子统计字典加到总的统计字典中

all_data = {bin: all_data[bin] + data[bin] for bin in all_data}

---

功能就是不断的把子统计数据合并到总的字典中，模拟一个counts展示一下

counts = [20]*100
bin_centers = {round(i/100, 3) + 0.005: 0 for i in range(100)}
data = {round(center, 3): count for center, count in zip(bin_centers, counts)}
all_data = {round(i/100, 3) + 0.005: 0 for i in range(100)}
all_data = {bin: all_data[bin] + data[bin] for bin in all_data}

报错data字典中没有0.034999999999999996这个key，那本来就不该有啊，那就是all_data中有，对比两个字典可以看出子字典多做了一次round保留3位小数

先打印下两个字典，不止0.035有误差，后面0.075还有好几个都对不上

---

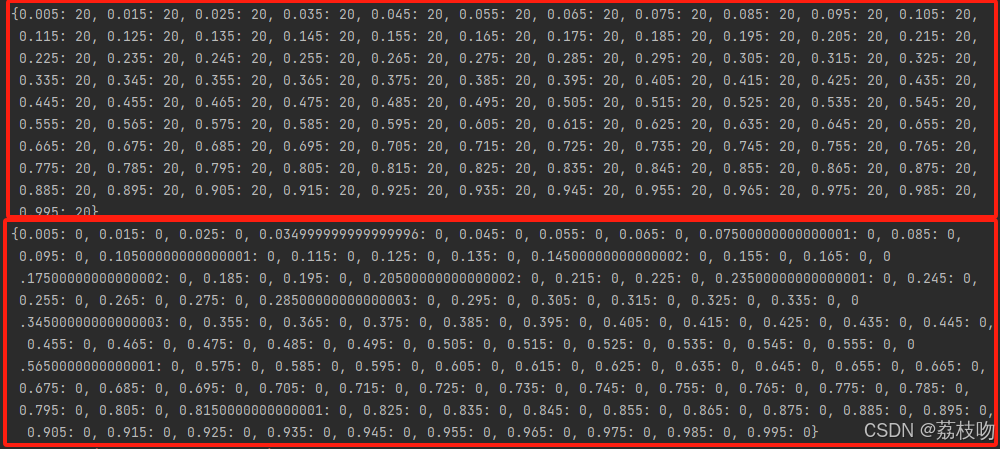
三、原因分析

直接原因就是子字典多做了一次round3，改变了小数有效值，底层原因就是IEEE 754规范，浮点数本身就是有误差的，有误差的计算结果有误差也很正常。
大部分十进制小数都是无法用二进制精确表达的，就像十进制也有无限循环小数和无线不循环小数，

但是，为什么有的行，比如0.005就没误差，有的用round保留后就不一致了？

在Java中，float是单精度浮点数,占4字节,精度约6-7位;double是双精度浮点数,占8字节,精度约15-16位
在python中，只有float，代表双精度浮点数，精度约15-16位，

0.005转化为二进制后对应的10进制误差在第16位以后了，类似于0.005000000000000012345678，12345678是我编的，保留三位后是0.005，相当于0.0050000000000000，他们对应的二进制是完全一样的，后面的误差无法在IEEE 754规范中表示了，
而round(3/100, 3) + 0.005=0.034999999999999996，误差在有效精度内，此时保留3位后为0.0350000000000000，保留的误差就对二进制数造成区别了

提一下round(x, n) 的函数内部流程
a) 把二进制浮点 x 转成“足够多位”的十进制字符串（内部算法，常用 Ryū 或 Dragon4）。
b) 按十进制规则保留 n 位小数。
c) 再把得到的十进制结果 重新转成最接近的二进制浮点数。

---

四、解决方案

浮点数精度有误差，计算就会累加误差，我这里误差主要是round造成的，所以要么给总的统计字典也补一次，更合理的是统一在计算后再进行round

counts = [20]*100
bin_centers = [round(i/100 + 0.005, 3) for i in range(100)]
data = {center: count for center, count in zip(bin_centers, counts)}
all_data = {round(i/100 + 0.005, 3): 0 for i in range(100)}
all_data = {bin: all_data[bin] + data[bin] for bin in all_data}

如果是精确计算，用decimal

from decimal import Decimala = Decimal('0.1')
b = Decimal('0.005')
print(a + b)        # 0.105（精确）

五、0.1+0.2和0.3？

测试的时候遇到的float经典例子

print(0.1+0.2)
print(0.3)
print(0.1+0.2==0.3)
print("===")
print(round(0.1+0.2,16))
print(round(0.1+0.2,16)==0.3)
print(round(0.1+0.2,17))
print(round(0.1+0.2,17)==0.3)

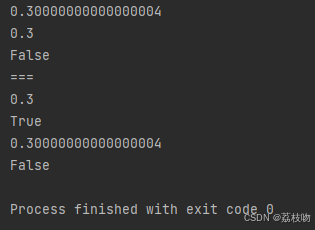
可以看出，0.1+0.2造成的误差在第17位，这个和与0.3对应的二进制还不相同，只有当round保留16位以内的时候，两个值才会相等。通过这个例子也可以更好的理解round的作用

参考文献

• 【回归本源】番外1-雷神之锤3的那段代码
• 当浮点数背叛了你——IEEE 754的精度陷阱与金融灾难
• IEEE-754 浮点数转换器
• float数据存储与转换：简单易懂

---

喜欢的点个关注吧><！祝你永无bug！

/*_ooOoo_o8888888o88" . "88(| -_- |)O\  =  /O____/`---'\____.'  \\|     |//  `./  \\|||  :  |||//  \/  _||||| -:- |||||-  \|   | \\\  -  /// |   || \_|  ''\---/''  |   |\  .-\__  `-`  ___/-. /___`. .'  /--.--\  `. . __."" '<  `.___\_<|>_/___.'  >'"".| | :  `- \`.;`\ _ /`;.`/ - ` : | |\  \ `-.   \_ __\ /__ _/   .-` /  /
======`-.____`-.___\_____/___.-`____.-'======`=---='
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^佛祖保佑       永无BUG
*/