信息安全各类加密算法解析

加密算法分类

• 常见应用较广的加密算法总的来说可以分为三类：
  • 对称加密算法
    
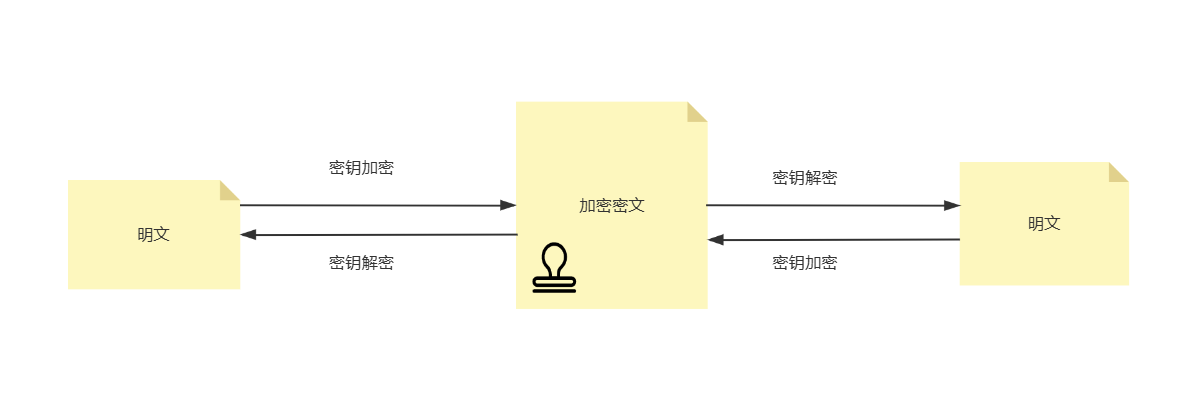
  • 非对称加密算法
    
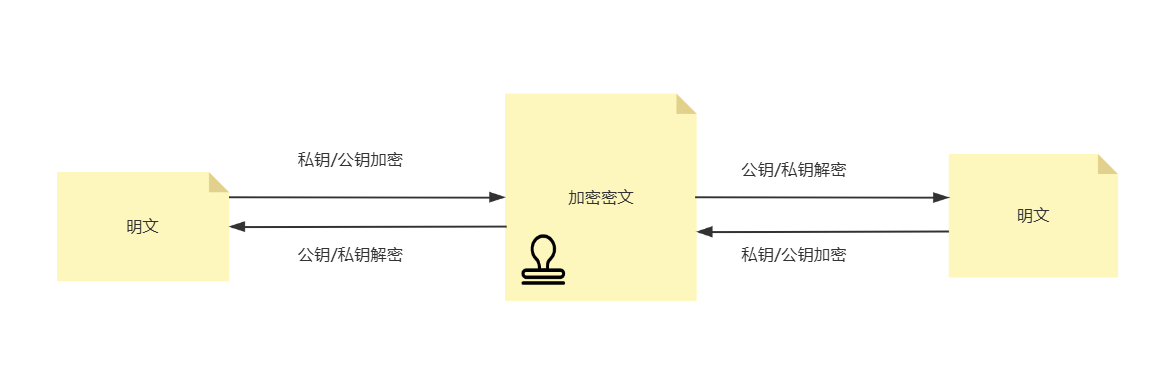
    公钥加密用于保证数据机密性：
    
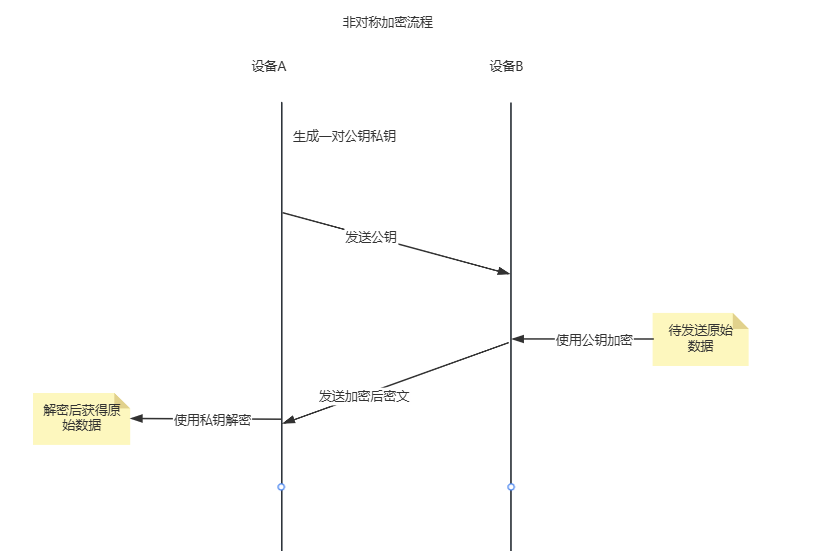
    私钥加密用于身份验证若用（私钥加密仅应用于数字签名，若私钥加密数据，任何人都可通过公开的公钥解密，无法保障机密性）：
    
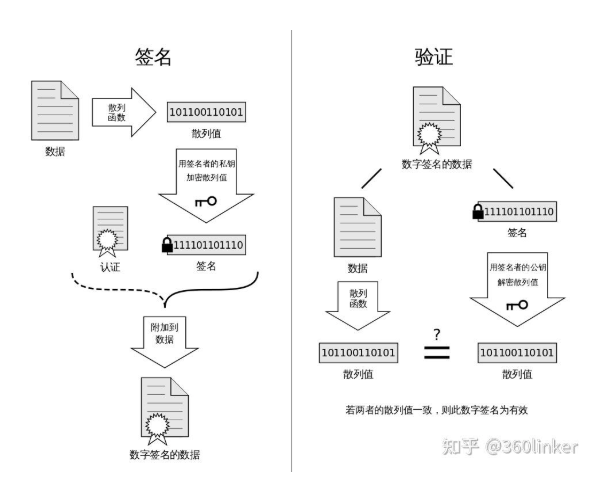
    该图片取自于以下文章：
    浅谈常见的七种加密算法及实现
  • 哈希算法（信息摘要算法）

---

以下是详细分类及典型算法：

一、对称加密算法（Symmetric Encryption）

核心特点：加密和解密使用同一把密钥（对称密钥），算法逻辑简单，加密效率极高。
解决问题：保障数据机密性（防止数据被窃取后泄露）。

1. 分组密码（Block Cipher）

将数据分成固定长度的 “块”（如 64 位、128 位），逐块加密，适合处理固定长度或长数据。

• 典型算法：
  • AES（Advanced Encryption Standard）：目前全球最主流的对称算法，支持 128/192/256 位密钥，分组长度 128 位，安全性高且效率极佳，应用于硬盘加密、HTTPS 数据传输等。
  • DES/3DES：DES 已被淘汰（56 位密钥太短），3DES 是其增强版（3 次 DES 加密），但效率低于 AES，逐步被替代。
  • 国密 SM4：我国自主分组密码，128 位密钥，分组长度 128 位，用于金融、车联网（如 V2X 通信加密）等场景，符合 GB 44495 等国标要求。
• 应用场景：文件加密（如 ZIP 加密）、数据库加密、车内 CAN 总线数据加密。

2. 流密码（Stream Cipher）

将数据视为连续的 “流”，逐位（或逐字节）加密，适合处理实时流数据（如语音、视频）。

• 典型算法：
  • RC4：曾广泛用于 WiFi（WEP）和 SSL，但因安全性漏洞（密钥流可预测）被淘汰。
  • ChaCha20：现代流密码，无 RC4 的漏洞，效率高，适合移动端和物联网（如 VPN 加密、即时通讯）。
• 应用场景：实时视频会议加密、物联网传感器数据传输。

二、非对称加密算法（Asymmetric Encryption）

核心特点：加密和解密使用一对不同但关联的密钥（公钥 + 私钥）：公钥公开（用于加密或验签），私钥保密（用于解密或签名）。算法依赖复杂数学难题（如大整数分解），安全性高但效率低。
解决问题：解决 “密钥交换” 难题（无需提前共享密钥）、实现身份认证和防抵赖（通过数字签名）。

1. 基于大整数分解难题

• 典型算法：
  • RSA：最经典的非对称算法，支持密钥长度 2048/4096 位，可用于加密（少量数据）和签名，应用于数字证书（如 HTTPS 证书）、SSH 登录等。
  • 缺点：密钥长度长（4096 位 RSA 的运算效率远低于 256 位 ECC），适合非实时场景。

2. 基于椭圆曲线离散对数难题（ECC）

• 典型算法：
  • ECC（Elliptic Curve Cryptography）：同等安全性下，密钥长度仅为 RSA 的 1/4（如 256 位 ECC≈2048 位 RSA），效率更高，适合资源受限设备（手机、物联网终端）。
  • 国密 SM2：我国自主 ECC 算法，支持签名、密钥交换，应用于电子签章、车联网身份认证（如 OBU 与 RSU 的双向认证），符合 GM/T 系列标准。
• 应用场景：移动支付（如支付宝 / 微信支付的身份验证）、V2X 通信的数字签名、区块链钱包（如比特币、以太坊的地址生成）。

三、哈希算法（Hash Function，消息摘要算法）

核心特点：将任意长度的输入数据转换为固定长度的输出（哈希值 / 摘要），且不可逆（无法从哈希值反推原数据）；输入微小变化会导致哈希值完全不同（雪崩效应）。
注意：哈希算法不是加密算法（无解密过程），但属于密码学核心技术，用于保障数据完整性（防篡改）。

1. 无密钥哈希（纯摘要）

• 典型算法：
  • SHA-256：输出 256 位哈希值，安全性高，应用于区块链（如比特币区块哈希）、软件完整性校验（如官网提供的安装包校验值）。
  • 国密 SM3：我国自主哈希算法，输出 256 位哈希值，用于数字签名的摘要生成（如 OTA 升级包的完整性校验）、政务数据存证等。
    MD5：已被淘汰（存在碰撞漏洞，可伪造相同哈希值的不同数据）。

2. 带密钥哈希（HMAC，哈希消息认证码）

在哈希过程中引入密钥，既保证完整性，又验证 “发送方是否拥有密钥”（类似轻量身份认证）。

• 典型算法：
  • HMAC-SHA256：结合 SHA-256 和密钥，用于 API 接口校验（如客户端请求的签名验证）、VPN 数据完整性校验。
  • HMAC-SM3：结合国密 SM3 和密钥，用于金融交易的完整性 + 身份双重验证。

总结：三类算法的核心定位

类别	核心功能	典型算法	一句话总结
对称加密	高效加密数据（机密性）	AES、SM4、ChaCha20	“一把钥匙加密解密，快且安全”
非对称加密	密钥交换、数字签名（身份）	RSA、ECC、SM2	“公私钥配对，慢但能验身份”
哈希算法	数据完整性校验（防篡改）	SHA-256、SM3、HMAC	“数据的指纹，不可逆防篡改”

实际应用中，三类算法常协同使用（如 HTTPS：非对称算法交换对称密钥→对称算法加密数据→哈希算法校验完整性），共同构建完整的安全体系。

加密算法的性能评价

一、运算效率（速度与吞吐量）

运算效率是最直观的性能指标，直接决定算法处理数据的 “快慢”，但需区分算法类型和测试场景（单次运算 / 批量数据）。

1.关键指标

• 吞吐量（Throughput）：单位时间内可加密 / 解密的数据量（通常以 Mbps/Gbps 或 MB/s 衡量），适用于对称加密 / 哈希算法（处理大数据流，如文件传输、云存储加密）。
• 单次运算耗时：完成一次加密 / 解密 / 签名 / 验签的时间（通常以 微秒（μs）/ 毫秒（ms） 衡量），适用于非对称加密算法（处理小数据，如密钥交换、数字签名）。

2.影响因素与实例

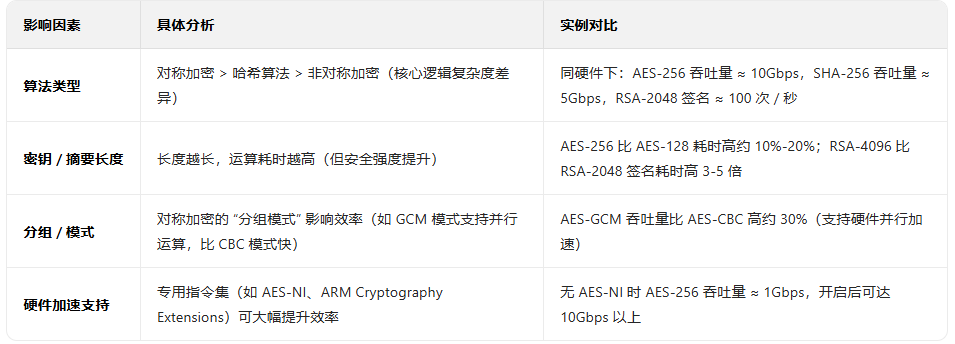
二、资源占用

在物联网（IoT）、嵌入式设备（如车联网 ECU）、移动端等资源受限场景中，“速度” 之外，CPU 使用率、内存消耗、功耗往往是更关键的性能指标。

1. 关键指标

• CPU 使用率：算法运行时占用的 CPU 资源比例（如单线程 / 多线程占用率），需避免因加密运算导致设备卡顿。
• 内存消耗（RAM）：算法运行时所需的临时存储空间（如缓存分组数据、密钥），资源受限设备（如传感器）通常仅支持 KB 级内存。
• 存储需求（ROM）：算法代码实现的体积（如嵌入式芯片的固件空间），需越小越好。
  功耗：算法运行时消耗的电量（如电池供电的物联网设备），运算越复杂，功耗越高。

2. 实例对比（资源友好性）
   

三、安全强度

“安全” 是加密算法的基石 —— 若安全强度不足（如易被破解），再高的效率也无意义。需通过 “安全强度”“抗攻击能力”“长期稳定性” 评估。

1. 关键指标

• 安全强度（Security Strength）：衡量算法抵御攻击的能力（以 “比特数” 表示，与密钥长度不完全等同），需符合行业标准（如 NIST、国密局要求）。
  示例：256 位 AES 的安全强度 = 256 位；2048 位 RSA 的安全强度≈112 位；256 位 ECC（P-256 曲线）的安全强度 = 128 位。
• 抗攻击能力：是否能抵御已知攻击（如暴力破解、差分攻击、侧信道攻击），是否有公开的安全漏洞。
• 长期稳定性：算法是否经过时间考验（如 AES 已使用 20 + 年，安全性得到全球验证），是否能对抗未来威胁（如量子计算）。

2. 安全强度与性能的平衡

• 误区：“密钥越长越安全”—— 需在 “安全” 与 “效率” 间平衡。例如：
  • 无需为普通文件加密选择 AES-256（AES-128 已足够安全，且效率更高）；
  • 金融场景需高安全强度，可选择 SM2（256 位 ECC，安全强度 128 位），而非 RSA-2048（安全强度仅 112 位，且效率低）。
• 抗量子能力：传统算法（RSA、ECC、AES）易被量子计算机破解，需关注 “后量子密码（PQC）”（如 NIST 推荐的 CRYSTALS-Kyber），但其当前效率低于传统算法，需权衡兼容性。

四、应用场景适配

脱离场景谈 “性能” 无意义 —— 需根据具体应用场景的核心需求，优先匹配对应维度的性能优势。

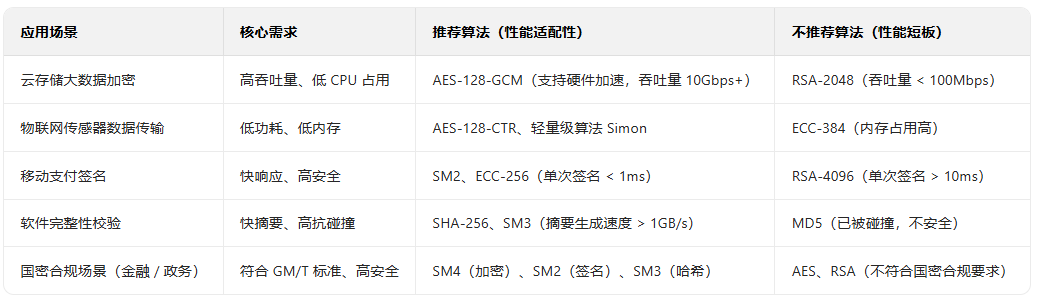
五、总结：评价逻辑

• 先定安全底线：排除有已知漏洞的算法（如 DES、MD5、RC4），确保安全强度符合场景需求（如普通场景≥128 位安全强度）；
• 再看场景需求：资源受限场景优先 “低占用”（如 ECC、轻量级 AES），大数据场景优先 “高吞吐量”（如 AES-GCM），合规场景优先 “标准兼容”（如国密 SM 系列）；
• 最后量化对比：通过工具测试运算效率、资源占用，选择 “安全达标、性能适配、成本可控” 的算法。

常用加密算法原理以及实现

汽车电子的加密算法需遵循 “场景适配 + 合规优先” 原则：

• 车内实时通信：优先 AES-128/SM4（高效）+ HMAC（认证），符合 Autosar SecOC 标准；
• 身份认证与签名：国际场景用 ECC/ECDSA，国内场景用 SM2，兼顾效率与合规；
• 完整性校验：SHA-256（国际）、SM3（国内）成为标配，支撑 OTA、日志等核心场景；
• 未来安全：后量子密码（Kyber、Dilithium）开始预研，适配汽车长生命周期需求。
  这些算法通过硬件安全模块（HSM）实现加速和密钥隔离，最终形成 “算法 + 硬件 + 标准” 三位一体的车载安全体系

---

一、AES原理

AES128、AES192、AES256算法核心内容一致，区别在于加密轮数分别为10轮、12轮、14轮，轮数多意味着加密过程更复杂，安全性更高，但也影响性能。

1.预处理

• 明文分组转换为状态矩阵
  128 位明文按 “列优先” 方式填入 4×4 矩阵（即先填第 1 列，再第 2 列……）：
  例如，16 字节明文 [b0, b1, b2, b3, b4, b5, b6, b7, b8, b9, b10, b11, b12, b13, b14, b15] 转换为：

[b0, b1, b2, b3, b4, b5, b6, b7, b8, b9, b10, b11, b12, b13, b14, b15] 转换为[ b0  b4  b8  b12 ]
[ b1  b5  b9  b13 ]
[ b2  b6  b10 b14 ]
[ b3  b7  b11 b15 ]

2. 密钥扩展（Key Expansion）
   128 位原始密钥需扩展为11 个子密钥（每轮加密使用 1 个，包括初始轮），每个子密钥也是 4×4 矩阵（16 字节）。扩展过程基于原始密钥生成后续子密钥，核心是 “轮常量”（Rcon）和 S 盒变换，确保子密钥的随机性和相关性低。

• 扩展规则：
  原始密钥作为第 1 个子密钥（W0）；
  后续子密钥（W1 至 W10）通过前一个子密钥的特定变换生成，涉及：
  ① 对前一子密钥的最后一列进行 “循环左移”；
  ② 用 S 盒替换每个字节；
  ③ 与轮常量（Rcon）异或；
  ④ 与前 4 列的子密钥异或，最终生成新的子密钥。

2.加密流程

AES-128 的加密过程包含11 轮操作：1 轮 “初始轮密钥加”+10 轮 “常规轮操作”，每轮操作均基于状态矩阵进行，最终输出 128 位密文。

• 1. 初始轮：轮密钥加（AddRoundKey）
     这是加密的第 1 步，仅包含 “轮密钥加” 操作：
     将状态矩阵与第 1 个子密钥（W0）的对应字节进行异或（XOR） 运算。
     例：状态矩阵中第 (i,j) 个字节 = 原始明文字节 (i,j) XOR 子密钥 W0 字节 (i,j)。
     作用：将明文与密钥初步混合，引入密钥信息。
• 2. 常规轮（第 1-9 轮）：4 步操作循环
     每轮包含 4 个依次执行的操作，共同实现 “混淆”（隐藏明文与密文的关系）和 “扩散”（使明文的微小变化影响整个密文）：
     （1）字节替换（SubBytes）
     用 AES 定义的S 盒（8×8 的置换表）对状态矩阵中的每个字节进行替换：
     每个字节（0-255）对应 S 盒中唯一的替换值（例如，字节 0x63 替换为 0xC5，具体查表）。

作用：通过非线性变换打破明文的统计规律，是 AES 安全性的核心。
（2）行移位（ShiftRows）
对状态矩阵的行进行循环左移，不同行移位次数不同：
第 0 行（首行）：不移位；
第 1 行：左移 1 位；
第 2 行：左移 2 位；
第 3 行：左移 3 位。

例：移位前矩阵：

[ a b c d ]
[ e f g h ]
[ i j k l ]
[ m n o p ]

移位后：

[ a b c d ]
[ f g h e ]  // 左移1位
[ k l i j ]  // 左移2位
[ p m n o ]  // 左移3位

作用：扩散数据，使单一行的信息分散到整个矩阵。
（3）列混合（MixColumns）
对状态矩阵的每一列进行有限域（GF (2⁸)）上的矩阵乘法，将列中 4 个字节混合为新的 4 个字节。
每个列向量与固定的混合矩阵相乘：

[ 02 03 01 01 ]
[ 01 02 03 01 ]
[ 01 01 02 03 ]
[ 03 01 01 02 ]

（注：乘法是有限域内的运算，例如 02×b 表示 “b 左移 1 位，若溢出则与 0x1b 异或”）

作用：进一步扩散列内数据，使单个字节的变化影响整个列。
（4）轮密钥加（AddRoundKey）
与初始轮逻辑相同，将当前状态矩阵与本轮子密钥（W1 至 W9）的对应字节异或。

作用：每轮引入新的密钥信息，增强加密强度。

• 3. 最后一轮（第 10 轮）：3 步操作
  最后一轮与常规轮的区别是去掉 “列混合（MixColumns）”，仅保留 3 步操作：
  SubBytes → ShiftRows → AddRoundKey（使用第 10 个子密钥 W10）。

原因：列混合是可逆操作，最后一轮去掉它可简化解密过程，同时不影响安全性

3.输出密文

最后一轮结束后，将 4×4 的状态矩阵按 “列优先” 方式重新转换为 16 字节的线性序列，即 128 位密文。

以下为图形化介绍： AES128加解密流程详细介绍

二、AES代码实现

1.c语言代码实现

#include <stdio.h>
#include <string.h>
#include <stdint.h>// -------------------------- AES-128 实现（ECB模式，用于验证）--------------------------
// 轮常量
static const uint32_t Rcon[11] = {0x00000000, 0x01000000, 0x02000000, 0x04000000, 0x08000000,0x10000000, 0x20000000, 0x40000000, 0x80000000, 0x1B000000, 0x36000000
};// S盒
static const uint8_t Sbox[256] = {0x63,0x7c,0x77,0x7b,0xf2,0x6b,0x6f,0xc5,0x30,0x01,0x67,0x2b,0xfe,0xd7,0xab,0x76,0xca,0x82,0xc9,0x7d,0xfa,0x59,0x47,0xf0,0xad,0xd4,0xa2,0xaf,0x9c,0xa4,0x72,0xc0,0xb7,0xfd,0x93,0x26,0x36,0x3f,0xf7,0xcc,0x34,0xa5,0xe5,0xf1,0x71,0xd8,0x31,0x15,0x04,0xc7,0x23,0xc3,0x18,0x96,0x05,0x9a,0x07,0x12,0x80,0xe2,0xeb,0x27,0xb2,0x75,0x09,0x83,0x2c,0x1a,0x1b,0x6e,0x5a,0xa0,0x52,0x3b,0xd6,0xb3,0x29,0xe3,0x2f,0x84,0x53,0xd1,0x00,0xed,0x20,0xfc,0xb1,0x5b,0x6a,0xcb,0xbe,0x39,0x4a,0x4c,0x58,0xcf,0xd0,0xef,0xaa,0xfb,0x43,0x4d,0x33,0x85,0x45,0xf9,0x02,0x7f,0x50,0x3c,0x9f,0xa8,0x51,0xa3,0x40,0x8f,0x92,0x9d,0x38,0xf5,0xbc,0xb6,0xda,0x21,0x10,0xff,0xf3,0xd2,0xcd,0x0c,0x13,0xec,0x5f,0x97,0x44,0x17,0xc4,0xa7,0x7e,0x3d,0x64,0x5d,0x19,0x73,0x60,0x81,0x4f,0xdc,0x22,0x2a,0x90,0x88,0x46,0xee,0xb8,0x14,0xde,0x5e,0x0b,0xdb,0xe0,0x32,0x3a,0x0a,0x49,0x06,0x24,0x5c,0xc2,0xd3,0xac,0x62,0x91,0x95,0xe4,0x79,0xe7,0xc8,0x37,0x6d,0x8d,0xd5,0x4e,0xa9,0x6c,0x56,0xf4,0xea,0x65,0x7a,0xae,0x08,0xba,0x78,0x25,0x2e,0x1c,0xa6,0xb4,0xc6,0xe8,0xdd,0x74,0x1f,0x4b,0xbd,0x8b,0x8a,0x70,0x3e,0xb5,0x66,0x48,0x03,0xf6,0x0e,0x61,0x35,0x57,0xb9,0x86,0xc1,0x1d,0x9e,0xe1,0xf8,0x98,0x11,0x69,0xd9,0x8e,0x94,0x9b,0x1e,0x87,0xe9,0xce,0x55,0x28,0xdf,0x8c,0xa1,0x89,0x0d,0xbf,0xe6,0x42,0x68,0x41,0x99,0x2d,0x0f,0xb0,0x54,0xbb,0x16
};// 逆S盒
static const uint8_t InvSbox[256] = {0x52,0x09,0x6a,0xd5,0x30,0x36,0xa5,0x38,0xbf,0x40,0xa3,0x9e,0x81,0xf3,0xd7,0xfb,0x7c,0xe3,0x39,0x82,0x9b,0x2f,0xff,0x87,0x34,0x8e,0x43,0x44,0xc4,0xde,0xe9,0xcb,0x54,0x7b,0x94,0x32,0xa6,0xc2,0x23,0x3d,0xee,0x4c,0x95,0x0b,0x42,0xfa,0xc3,0x4e,0x08,0x2e,0xa1,0x66,0x28,0xd9,0x24,0xb2,0x76,0x5b,0xa2,0x49,0x6d,0x8b,0xd1,0x25,0x72,0xf8,0xf6,0x64,0x86,0x68,0x98,0x16,0xd4,0xa4,0x5c,0xcc,0x5d,0x65,0xb6,0x92,0x6c,0x70,0x48,0x50,0xfd,0xed,0xb9,0xda,0x5e,0x15,0x46,0x57,0xa7,0x8d,0x9d,0x84,0x90,0xd8,0xab,0x00,0x8c,0xbc,0xd3,0x0a,0xf7,0xe4,0x58,0x05,0xb8,0xb3,0x45,0x06,0xd0,0x2c,0x1e,0x8f,0xca,0x3f,0x0f,0x02,0xc1,0xaf,0xbd,0x03,0x01,0x13,0x8a,0x6b,0x3a,0x91,0x11,0x41,0x4f,0x67,0xdc,0xea,0x97,0xf2,0xcf,0xce,0xf0,0xb4,0xe6,0x73,0x96,0xac,0x74,0x22,0xe7,0xad,0x35,0x85,0xe2,0xf9,0x37,0xe8,0x1c,0x75,0xdf,0x6e,0x47,0xf1,0x1a,0x71,0x1d,0x29,0xc5,0x89,0x6f,0xb7,0x62,0x0e,0xaa,0x18,0xbe,0x1b,0xfc,0x56,0x3e,0x4b,0xc6,0xd2,0x79,0x20,0x9a,0xdb,0xc0,0xfe,0x78,0xcd,0x5a,0xf4,0x1f,0xdd,0xa8,0x33,0x88,0x07,0xc7,0x31,0xb1,0x12,0x10,0x59,0x27,0x80,0xec,0x5f,0x60,0x51,0x7f,0xa9,0x19,0xb5,0x4a,0x0d,0x2d,0xe5,0x7a,0x9f,0x93,0xc9,0x9c,0xef,0xa0,0xe0,0x3b,0x4d,0xae,0x2a,0xf5,0xb0,0xc8,0xeb,0xbb,0x3c,0x83,0x53,0x99,0x61,0x17,0x2b,0x04,0x7e,0xba,0x77,0xd6,0x26,0xe1,0x69,0x14,0x63,0x55,0x21,0x0c,0x7d
};// 字节替换
static void SubBytes(uint8_t state[4][4]) {for (int i = 0; i < 4; i++)for (int j = 0; j < 4; j++)state[i][j] = Sbox[state[i][j]];
}// 逆字节替换
static void InvSubBytes(uint8_t state[4][4]) {for (int i = 0; i < 4; i++)for (int j = 0; j < 4; j++)state[i][j] = InvSbox[state[i][j]];
}// 行移位
static void ShiftRows(uint8_t state[4][4]) {uint8_t temp;// 第二行左移1temp = state[1][0];state[1][0] = state[1][1];state[1][1] = state[1][2];state[1][2] = state[1][3];state[1][3] = temp;// 第三行左移2temp = state[2][0];state[2][0] = state[2][2];state[2][2] = temp;temp = state[2][1];state[2][1] = state[2][3];state[2][3] = temp;// 第四行左移3temp = state[3][3];state[3][3] = state[3][2];state[3][2] = state[3][1];state[3][1] = state[3][0];state[3][0] = temp;
}// 逆行移位
static void InvShiftRows(uint8_t state[4][4]) {uint8_t temp;// 第二行右移1temp = state[1][3];state[1][3] = state[1][2];state[1][2] = state[1][1];state[1][1] = state[1][0];state[1][0] = temp;// 第三行右移2temp = state[2][0];state[2][0] = state[2][2];state[2][2] = temp;temp = state[2][1];state[2][1] = state[2][3];state[2][3] = temp;// 第四行右移3temp = state[3][0];state[3][0] = state[3][1];state[3][1] = state[3][2];state[3][2] = state[3][3];state[3][3] = temp;
}// 有限域乘法
static uint8_t GaloisMultiply(uint8_t a, uint8_t b) {uint8_t p = 0;for (int i = 0; i < 8; i++) {if (b & 1) p ^= a;uint8_t hi = a & 0x80;a <<= 1;if (hi) a ^= 0x1b; // x^8 + x^4 + x^3 + x + 1b >>= 1;}return p;
}// 列混合
static void MixColumns(uint8_t state[4][4]) {uint8_t temp[4];for (int i = 0; i < 4; i++) {temp[0] = GaloisMultiply(0x02, state[0][i]) ^ GaloisMultiply(0x03, state[1][i]) ^ state[2][i] ^ state[3][i];temp[1] = state[0][i] ^ GaloisMultiply(0x02, state[1][i]) ^ GaloisMultiply(0x03, state[2][i]) ^ state[3][i];temp[2] = state[0][i] ^ state[1][i] ^ GaloisMultiply(0x02, state[2][i]) ^ GaloisMultiply(0x03, state[3][i]);temp[3] = GaloisMultiply(0x03, state[0][i]) ^ state[1][i] ^ state[2][i] ^ GaloisMultiply(0x02, state[3][i]);for (int j = 0; j < 4; j++) state[j][i] = temp[j];}
}// 逆列混合
static void InvMixColumns(uint8_t state[4][4]) {uint8_t temp[4];for (int i = 0; i < 4; i++) {temp[0] = GaloisMultiply(0x0e, state[0][i]) ^ GaloisMultiply(0x0b, state[1][i]) ^ GaloisMultiply(0x0d, state[2][i]) ^ GaloisMultiply(0x09, state[3][i]);temp[1] = GaloisMultiply(0x09, state[0][i]) ^ GaloisMultiply(0x0e, state[1][i]) ^ GaloisMultiply(0x0b, state[2][i]) ^ GaloisMultiply(0x0d, state[3][i]);temp[2] = GaloisMultiply(0x0d, state[0][i]) ^ GaloisMultiply(0x09, state[1][i]) ^ GaloisMultiply(0x0e, state[2][i]) ^ GaloisMultiply(0x0b, state[3][i]);temp[3] = GaloisMultiply(0x0b, state[0][i]) ^ GaloisMultiply(0x0d, state[1][i]) ^ GaloisMultiply(0x09, state[2][i]) ^ GaloisMultiply(0x0e, state[3][i]);for (int j = 0; j < 4; j++) state[j][i] = temp[j];}
}// 密钥扩展
static void KeyExpansion(const uint8_t key[16], uint8_t w[4][44]) {uint8_t temp[4];// 初始密钥for (int i = 0; i < 4; i++)for (int j = 0; j < 4; j++)w[j][i] = key[i*4 + j];for (int i = 4; i < 44; i++) {// 保存前一列for (int j = 0; j < 4; j++) temp[j] = w[j][i-1];// 列移位和S盒变换if (i % 4 == 0) {uint8_t t = temp[0];temp[0] = Sbox[temp[1]];temp[1] = Sbox[temp[2]];temp[2] = Sbox[temp[3]];temp[3] = Sbox[t];// 异或轮常量for (int j = 0; j < 4; j++) temp[j] ^= (Rcon[i/4] >> (24 - j*8)) & 0xff;}// 计算当前列for (int j = 0; j < 4; j++)w[j][i] = w[j][i-4] ^ temp[j];}
}// 轮密钥加
static void AddRoundKey(uint8_t state[4][4], const uint8_t w[4][44], int round) {for (int i = 0; i < 4; i++)for (int j = 0; j < 4; j++)state[i][j] ^= w[i][round*4 + j];
}// AES-128加密（ECB模式，16字节明文输入）
void aes128_encrypt(const uint8_t plaintext[16], const uint8_t key[16], uint8_t ciphertext[16]) {uint8_t state[4][4];uint8_t w[4][44];// 初始化状态矩阵for (int i = 0; i < 4; i++)for (int j = 0; j < 4; j++)state[j][i] = plaintext[i*4 + j];// 密钥扩展KeyExpansion(key, w);// 初始轮密钥加AddRoundKey(state, w, 0);// 9轮迭代for (int round = 1; round < 10; round++) {SubBytes(state);ShiftRows(state);MixColumns(state);AddRoundKey(state, w, round);}// 第10轮（无列混合）SubBytes(state);ShiftRows(state);AddRoundKey(state, w, 10);// 输出密文for (int i = 0; i < 4; i++)for (int j = 0; j < 4; j++)ciphertext[i*4 + j] = state[j][i];
}// AES-128解密（ECB模式，16字节密文输入）
void aes128_decrypt(const uint8_t ciphertext[16], const uint8_t key[16], uint8_t plaintext[16]) {uint8_t state[4][4];uint8_t w[4][44];// 初始化状态矩阵for (int i = 0; i < 4; i++)for (int j = 0; j < 4; j++)state[j][i] = ciphertext[i*4 + j];// 密钥扩展KeyExpansion(key, w);// 初始轮密钥加（第10轮密钥）AddRoundKey(state, w, 10);// 9轮迭代for (int round = 9; round > 0; round--) {InvShiftRows(state);InvSubBytes(state);AddRoundKey(state, w, round);InvMixColumns(state);}// 最后一轮（无逆列混合）InvShiftRows(state);InvSubBytes(state);AddRoundKey(state, w, 0);// 输出明文for (int i = 0; i < 4; i++)for (int j = 0; j < 4; j++)plaintext[i*4 + j] = state[j][i];
}
// -------------------------- 测试函数 --------------------------
// 打印十六进制数据
void print_hex(const char *name, const uint8_t *data, size_t len) {printf("%s: ", name);for (size_t i = 0; i < len; i++) {printf("%02x", data[i]);}printf("\n");
}// 比较两个缓冲区是否相等
int buffer_equal(const uint8_t *a, const uint8_t *b, size_t len) {for (size_t i = 0; i < len; i++) {if (a[i] != b[i]) return 0;}return 1;
}
// AES-128测试（使用NIST标准测试向量）
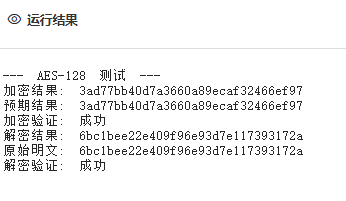
void test_aes128() {printf("\n--- AES-128 测试 ---\n");// 测试向量: NIST SP 800-38Auint8_t key[16] = {0x2b,0x7e,0x15,0x16,0x28,0xae,0xd2,0xa6,0xab,0xf7,0x15,0x88,0x09,0xcf,0x4f,0x3c};uint8_t plaintext[16] = {0x6b,0xc1,0xbe,0xe2,0x2e,0x40,0x9f,0x96,0xe9,0x3d,0x7e,0x11,0x73,0x93,0x17,0x2a};uint8_t expected_cipher[16] = {0x3a,0xd7,0x7b,0xb4,0x0d,0x7a,0x36,0x60,0xa8,0x9e,0xca,0xf3,0x24,0x66,0xef,0x97};uint8_t ciphertext[16];uint8_t decrypted[16];aes128_encrypt(plaintext, key, ciphertext);print_hex("加密结果", ciphertext, 16);print_hex("预期结果", expected_cipher, 16);printf("加密验证: %s\n", buffer_equal(ciphertext, expected_cipher, 16) ? "成功" : "失败");aes128_decrypt(ciphertext, key, decrypted);print_hex("解密结果", decrypted, 16);print_hex("原始明文", plaintext, 16);printf("解密验证: %s\n", buffer_equal(decrypted, plaintext, 16) ? "成功" : "失败");
}int main() {test_aes128();   // 测试AES-128加密解密return 0;
}

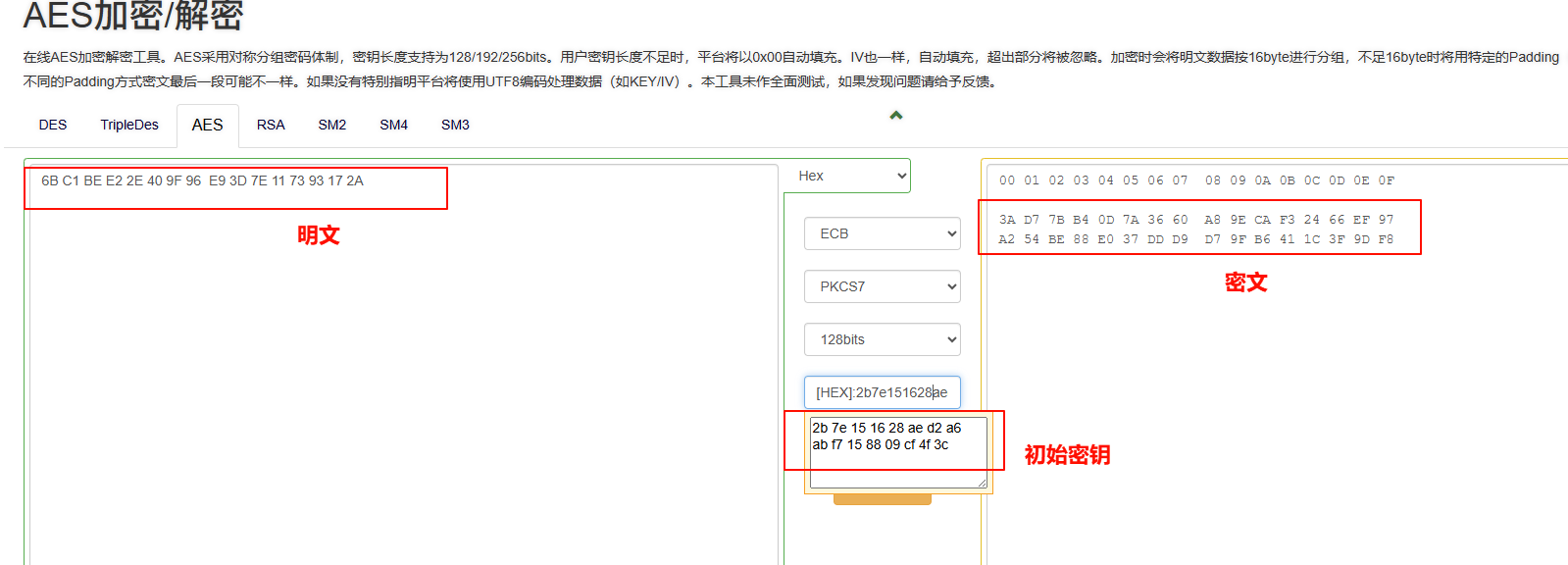
2.测试结果

加密算法在线测试