基于全参考图的质量评价均方误差MSE、峰值信噪比PSNR
1 均方误差(Mean Square Error, MSE)
1.1 基本概念
均方误差MSE是指样本估计值与其实值之差平方的数学期望值,是一种非常经典的计算图像失真程度的指标。
原图像与仿真图像可以用x和y表示,原图像与仿真图像的第i、j个像素的灰度像索值用xij和xij分别 表示,其中i=l,2,...,M;j=l,2,...,N。M、N分别为图像总的行和列像素数,因此两个图像之间的均方误差MSE就可以定义为式:
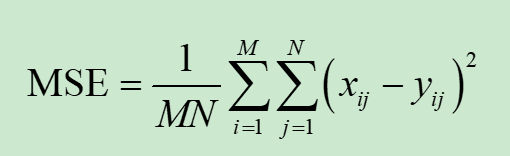
MSE理论取值范围为[0,∞),值越大,表示失真越严重。
1.2 归一化
在实际机器学习或深度学习中需要将其归一化到[0,1]。 具体归一化Matlab代码如下:
function normalized_mse=nmse(mse_value, max_mse, min_mse)% 设置合理的mse范围if nargin < 2max_mse = 1000; % 通常认为mse>1000表示极差质量min_mse = 0; % mse=0表示极高质量end% 处理无穷大的情况if isinf(mse_value)normalized_mse = 1.0;return;end% 归一化到0~1范围normalized_mse = 1-(mse_value - min_mse) / (max_mse - min_mse);% 确保结果在0~1之间normalized_mse = max(0, min(1, normalized_mse));
end2 峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)
2.1 基本概念
峰值信噪比PSNR实际上是均方误差MSE的一种变形,表示的是一个信号最大功率与影响它的精度的破坏性噪声功率的比值。对于大部分图像信号来说,通常具有非常宽的动态范围,所以一般会对其取对数。因此原图像和仿其图像的PSNR就可以定义为式:
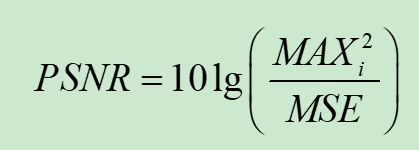
其中,MAXi表示图像像素点定义的最大值,对于8bit灰度图像其值为255。
2.2 评价标准与归一化
PSNR行业经验普遍认可的评价标准如下:
| PSNR范围(dB) | 对应MSE值 | 图像质量评价 |
| >40 | 6.5025 | 极好(肉眼不可辨差异) |
| 30~40 | 6.5025~65.025 | 良好(可接受质量) |
| 20~30 | 65.025~650.25 | 较差(明显失真) |
| <20 | 650.25 | 严重失真(不可接受) |
在实际机器学习或深度学习中需要将其归一化到[0,1]。 具体归一化Matlab代码如下:
function normalized_psnr=npsnr(psnr_value, max_psnr, min_psnr)% 设置合理的PSNR范围if nargin < 2max_psnr = 50; % 通常认为PSNR>50表示极高质量min_psnr = 0; % PSNR=0表示极差质量end% 处理无穷大的情况if isinf(psnr_value)normalized_psnr = 1.0;return;end% 归一化到0~1范围normalized_psnr = (psnr_value - min_psnr) / (max_psnr - min_psnr);% 确保结果在0~1之间normalized_psnr = max(0, min(1, normalized_psnr));
end3 实验结果
实验验证选择TID2013数据集的第一组参考图像和失真图像(转化为灰度图像)进行计算:

(a)参考图像

(b)失真图像
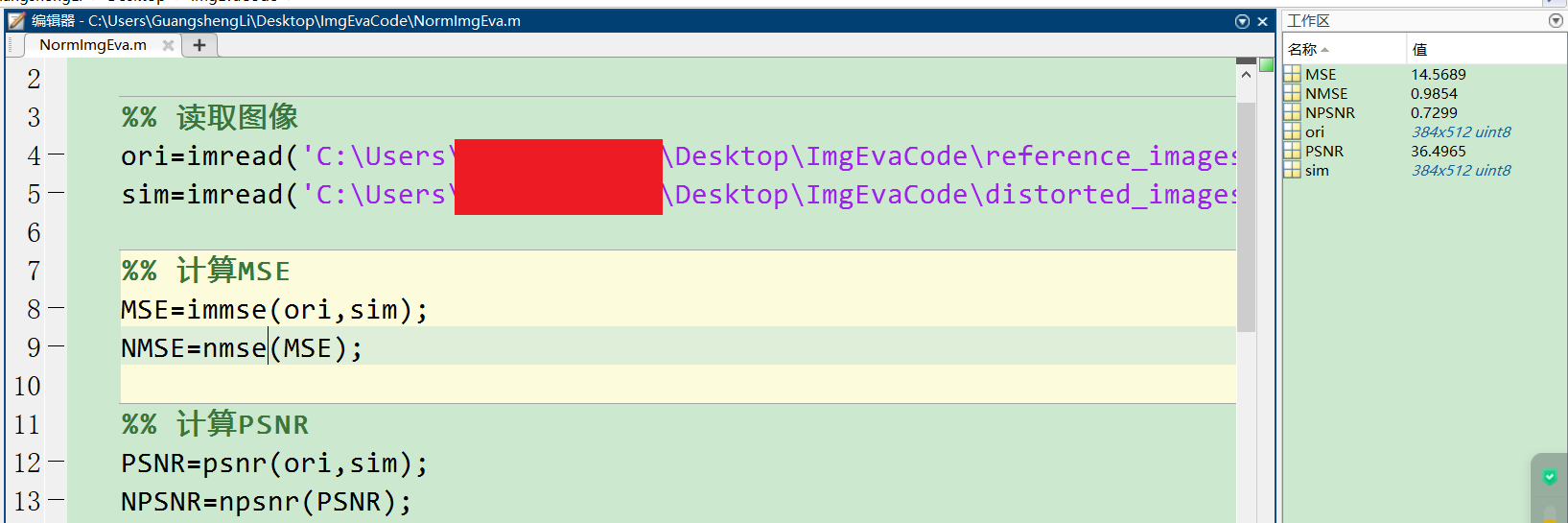
运行结果:
MSE:14.5689
归一化MSE:0.9854
PSNR:36.4965
归一化PSNR:0.7299。
