螺旋曲面交线投影切线角度计算与分析
在几何建模与计算机视觉领域,计算两个曲面交线在特定平面上的投影切线角度是一个常见问题。本文将基于给定的参数和方程,详细分析如何求解方程 F1(xd,yd,zd)=0F1(xd, yd, zd) = 0F1(xd,yd,zd)=0 和 F2=0F2 = 0F2=0 的交线在 ydydyd-zdzdzd 平面上的投影在坐标原点处的切线角度。
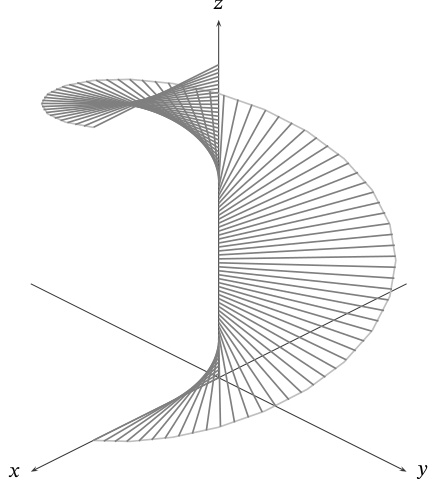
理论基础
坐标变换与方程定义
首先定义坐标变换矩阵和基本方程。给定变换矩阵:
RT=[100Bsinϕ/tanθ0100001−Bsinϕ0001]R_T = \begin{bmatrix} 1 & 0 & 0 & B\sin\phi/\tan\theta \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & -B\sin\phi \\ 0 & 0 & 0 & 1 \end{bmatrix}RT= 100001000010Bsinϕ/tanθ0−Bsinϕ1
Rϕ=[cosϕ0−sinϕ00100sinϕ0cosϕ00001]R_\phi = \begin{bmatrix} \cos\phi & 0 & -\sin\phi & 0 \\ 0 & 1 & 0 & 0 \\ \sin\phi & 0 & \cos\phi & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}Rϕ= cosϕ0sinϕ00100−sinϕ0cosϕ00001
Rβ=[10000cosβsinβ00−sinβcosβ00001]R_\beta = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\beta & \sin\beta & 0 \\ 0 & -\sin\beta & \cos\beta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}Rβ= 10000cosβ−sinβ00sin
