当前位置：首页 > web >正文

直线拟合方法全景解析：最小二乘、正交回归与 RANSAC

web 2025/8/28 8:18:26

本文系统梳理了直线拟合的三种常见方法：常规最小二乘（OLS）、正交回归（Total Least Squares，TLS，又称最小化垂直距离）以及具备抗离群点能力的 RANSAC。我们从线性代数的投影原理出发，推导出闭式解，并给出工程实现建议及示例代码。希望通过本文，读者能全面理解直线拟合的数学本质与实际应用要点。

一、常规最小二乘法（OLS）拟合直线

1 分析方法

已知数据点为

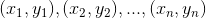
，欲拟合直线

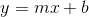
，则有最小化：

。

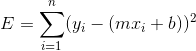
使用矩阵表示，令

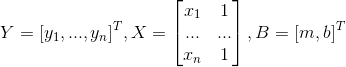
，则有：

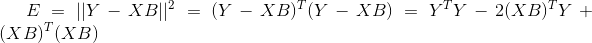
X, Y已知，要使E最小化，则向量B求导等于零：

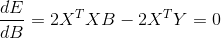
，整理得：

。

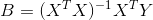
2 线性代数方法

在分析方法中，使用最小误差法拟合直线。这里还可以使用线性代数中正交原理得到相同结果。

1）线到线上投影

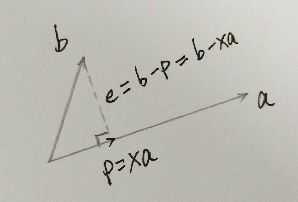
如上图所示，b 到 a 的投影为 p = xa，由于 e 与 a 垂直，有 (b - xa)a = 0，未知数为 x。

求解方程得

，

。

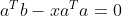
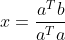
带入 x 值，计算出 b 到 a 的投影为

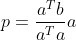
，投影矩阵为

，

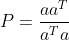
根据投影矩阵，b 到 a 的投影可重写为

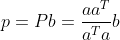
。给定一个向量，可以求解出投影到该向量的投影矩阵，任意向量到给定向量的投影即为 Pb 。

2）线到面上投影

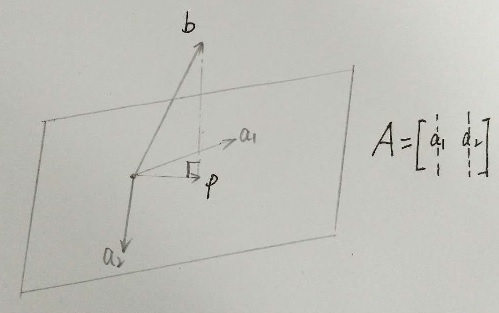
如上图所示，超平面为矩阵 A 的列空间构成（为了可视化，上图限制为二维平面，但结论对 N 维平面均适用），b 到平面 A 的投影为 p ，p 可表示为

。

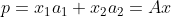
类似线到线投影，e = b - p，e 垂直于平面 A，有：

，

。

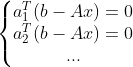
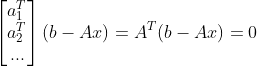
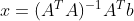
带入 x 计算出 b 到平面 A 的投影为

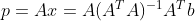
，投影矩阵为

。

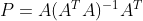
根据投影矩阵， b 到平面 A 的投影可重写为

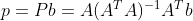
。给定一个矩阵，可以求解出投影到该矩阵列空间构成的超平面上的投影矩阵，任意向量到给定矩阵列空间构成的超平面上的投影为 Pb。

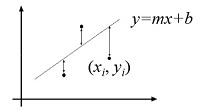
3）直线拟合

设直线方程为 y = kx + b，对于任意点 (x,y)，带入直线方程得：

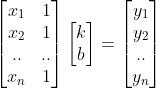
，当向量

落在矩阵

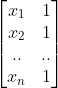
列空间构成得超平面外时，方程组无解。这也正是最小二乘法需要解决得问题。

将向量

投影到矩阵

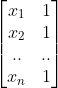
列空间构成的超平面，根据线到面上投影，可以寻找投影向量 p，改写方程为

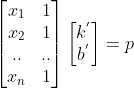
，该方程组有解。

使用

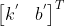
作为原方程的最佳近似解，带入

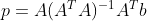
，解得

。

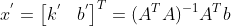
对于方程组 Ax=b，当 b 不在矩阵 A 的列空间时，无法求得 x 精确解，但可以求得 x 的近似解，使得

。

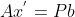
实际运算中，并不需要特意求解 P，只需对方程组做如下变换即可：

。

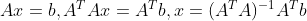
二、最小化垂直距离（Total Least Squares / 正交回归）

常规最小二乘法有如下问题：

1）数据点旋转后，求解得直线是变化的；

2）垂直直线无法求解；

通过修改 E 表达式，可以克服以上问题，如下图：

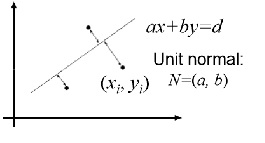
假设

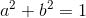
，图中直线方程

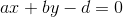
已经归一化，任意点

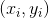
到直线的距离为

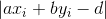
，则有最小化：

。

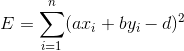
上式中，a,b,d 均为未知量，首先对求偏导，有：

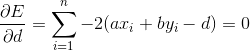
，整理得：

，

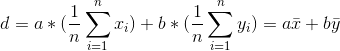
将d代入E中得：

。

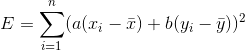
使用矩阵表示，令

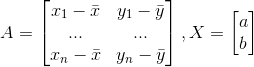
，有：

，

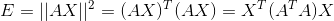
对X求导，可得：

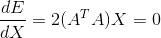
，求解二元一次方程组

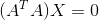
可计算处拟合直线。

三、RANSAC：抗离群点的鲁棒拟合

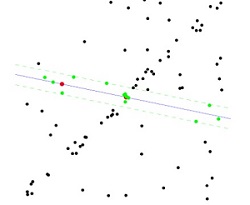
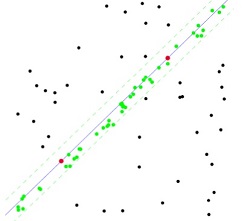
如上图所示，少数离群点可使拟合出现较大偏差。因此，应该使用一些逻辑来降低离群点干扰，具体措施如下：

1）随机选取一个子集，使用最小二乘法拟合直线；

2）在规定得误差范围内计算合群点；

3）多次选取不同的子集，继续1）2）操作；

4）选择合群点最多模型作为拟合初步结果，使用该模型下所有合群点重新拟合直线，得到最终结果。

四、方法比较

特性	OLS（纵向残差）	TLS/正交回归（垂直残差）	RANSAC
旋转不变性	否	是	是
垂直直线可处理性	差	好	好
抗离群能力	弱	弱	强
计算速度	快	快	较慢（取决于迭代次数）
闭式解	有	有	否（最终用 OLS/TLS）

五、实现示例

5.1 Python / NumPy

import numpy as npdef fit_line_ols(x, y):X = np.column_stack([x, np.ones_like(x)])beta, *_ = np.linalg.lstsq(X, y, rcond=None)return beta[0], beta[1]def fit_line_tls(x, y):x, y = np.asarray(x), np.asarray(y)xm, ym = x.mean(), y.mean()Xc = np.column_stack([x - xm, y - ym])S = Xc.T @ Xcw, v = np.linalg.eigh(S)a, b = v[:, 0]d = -a * xm - b * ymreturn a, b, d

5.2 C++ / Eigen

#include <Eigen/Dense>
#include <vector>// OLS: y = kx + b
std::pair<double,double> fitLineOLS(const std::vector<double>& x,const std::vector<double>& y){using namespace Eigen;int n = x.size();MatrixXd X(n,2);VectorXd Y(n);for(int i=0;i<n;++i){ X(i,0)=x[i]; X(i,1)=1.0; Y(i)=y[i]; }VectorXd beta = X.colPivHouseholderQr().solve(Y);return {beta(0), beta(1)};
}// TLS: ax + by + d = 0, a^2 + b^2 = 1
struct LineTLS { double a,b,d; };LineTLS fitLineTLS(const std::vector<double>& x,const std::vector<double>& y){using namespace Eigen;int n = x.size();double xm=0, ym=0; for(int i=0;i<n;++i){ xm+=x[i]; ym+=y[i]; }xm/=n; ym/=n;Matrix2d S = Matrix2d::Zero();for(int i=0;i<n;++i){double dx=x[i]-xm, dy=y[i]-ym;S(0,0)+=dx*dx; S(0,1)+=dx*dy;S(1,0)+=dx*dy; S(1,1)+=dy*dy;}SelfAdjointEigenSolver<Matrix2d> es(S);Vector2d nvec = es.eigenvectors().col(0);double a=nvec(0), b=nvec(1);double d = -a*xm - b*ym;return {a,b,d};
}