深度学习的正则化
深度学习正则化
学习⽬标
知道 L2 正则化与 L1 正则化的⽅法
知道随机失活 droupout 的应⽤
知道提前停⽌的使⽤⽅法
知道 BN 层的使⽤⽅法

在设计机器学习算法时不仅要求在训练集上误差⼩,⽽且希望在新样本上的泛化能⼒强。许多机器学习算法都采⽤相关的策略来减⼩测试误差,这些策略被统称为正则化。因为神经⽹络的强⼤的表示能⼒经常遇到过拟合,所以需要使⽤不同形式的正则化策略。
正则化通过对算法的修改来减少泛化误差,⽬前在深度学习中使⽤较多的策略有参数范数惩罚,提前终⽌, DropOut 等,接下来我们对其进⾏详细的介绍。
1. L1与L2正则化(回顾)
L1 和 L2 是最常⻅的正则化⽅法。它们在损失函数( cost function )中增加⼀个正则项,由于添加了这个正则化项,权重矩阵的值减⼩,因为它假定具有更⼩权重矩阵的神经⽹络导致更简单的模型。 因此,它也会在⼀定程度上减少过拟合。然⽽,这个正则化项在 L1 和 L2 中是不同的。
L2 正则化

这⾥的 λ 是正则化参数,它是⼀个需要优化的超参数。 L2 正则化⼜称为权重衰减,因为其导致权重趋向于 0 (但不全是 0 )
L1 正则化

这⾥,我们惩罚权重矩阵的绝对值。其中, λ 为正则化参数,是超参数,不同于 L2 ,权重值可能被减少到 0. 因此, L1 对于压缩模型很有⽤。其它情况下,⼀般选择优先选择 L2 正则化。
2.Dropout正则化
dropout 是在深度学习领域最常⽤的正则化技术。 Dropout 的原理很简单:假设我们的神经⽹络结构如下所示,在每个迭代过程中,随机选择某些节点,并且删除前向和后向连接。

因此,每个迭代过程都会有不同的节点组合,从⽽导致不同的输出,这可以看成机器学习中的集成⽅法( ensemble technique )。集成模型⼀般优于单⼀模型,因为它们可以捕获更多的随机性。相似地, dropout 使得神经⽹络模型优于正常的模型。
代码分析
# 这行代码创建了一个 Dropout 层,失活概率为 0.4,即在训练过程中,每个神经元有 40% 的概率被设置为零。
dropout = nn.Dropout(p = 0.4)
# 创建了一个形状为 (1, 4) 的输入张量,值在 0 到 9 之间,并将其转换为浮点数
inputs = torch.randint(0,10,size=(1,4)).float()
# 创建了一个线性层,输入特征维度为 4,输出特征维度为 5
layer = nn.Linear(4,5)
y = layer(inputs)
print("未失活FC层的输出结果:\n", y)
y = dropout(y)
print("失活后FC层的输出结果:\n", y)"""
未失活FC层的输出结果:tensor([[-5.5901, 1.1587, 2.6764, -3.0007, 5.9511]],grad_fn=<AddmmBackward0>)
失活后FC层的输出结果:tensor([[-0.0000, 0.0000, 4.4607, -5.0012, 0.0000]], grad_fn=<MulBackward0>)
"""3.提前停⽌
提前停⽌( early stopping )是将⼀部分训练集作为验证集( validationset )。 当验证集的性能越来越差时或者性能不再提升,则⽴即停⽌对该模型的训练。 这被称为提前停⽌。

在上图中,在虚线处停⽌模型的训练,此时模型开始在训练数据上过拟合。
1. 定义提前停止的逻辑
提前停止需要设置以下参数:
- patience:允许模型在验证集上性能没有提升的最大 epoch 数。
- min_delta:验证集性能提升的最小阈值,只有当提升超过此值时才认为性能有改善。
- best_val_loss:记录当前最佳的验证损失。
- patience_counter:记录验证损失没有改善的连续 epoch 数。
import torch
import torch.nn as nn
import torch.optim as optim# 定义模型
model = nn.Linear(10, 1) # 示例模型
criterion = nn.MSELoss() # 损失函数
optimizer = optim.SGD(model.parameters(), lr=0.01) # 优化器# 提前停止的参数
early_stopping_patience = 5 # 耐心值
min_delta = 0.001 # 最小性能提升
best_val_loss = float('inf') # 初始化最佳验证损失
patience_counter = 0 # 耐心计数器# 模拟训练和验证数据
train_loader = [(torch.randn(10, 10), torch.randn(10, 1)) for _ in range(100)]
val_loader = [(torch.randn(10, 10), torch.randn(10, 1)) for _ in range(20)]def validate(model, val_loader, criterion):model.eval() # 设置为评估模式total_loss = 0with torch.no_grad():for inputs, targets in val_loader:outputs = model(inputs)loss = criterion(outputs, targets)total_loss += loss.item()return total_loss / len(val_loader)# 训练循环
num_epochs = 100
for epoch in range(num_epochs):model.train() # 设置为训练模式train_loss = 0for inputs, targets in train_loader:optimizer.zero_grad()outputs = model(inputs)loss = criterion(outputs, targets)loss.backward()optimizer.step()train_loss += loss.item()train_loss /= len(train_loader)# 验证阶段val_loss = validate(model, val_loader, criterion)print(f"Epoch {epoch+1}/{num_epochs}, Train Loss: {train_loss:.4f}, Val Loss: {val_loss:.4f}")# 提前停止逻辑if val_loss < best_val_loss - min_delta:best_val_loss = val_losstorch.save(model.state_dict(), 'best_model.pth') # 保存最佳模型patience_counter = 0 # 重置耐心计数器else:patience_counter += 1if patience_counter >= early_stopping_patience:print("Early stopping triggered...")break4. 批标准化(BN层)
批标准化 (BN 层 ,Batch Normalization) 是 2015 年提出的⼀种⽅法,在进⾏深度⽹络训练时,⼤多会采取这种算法,与全连接层⼀样, BN 层也是属于⽹络中的⼀层。
批标准化(Batch Normalization,简称BN)是一种在深度神经网络中常用的技巧,旨在解决训练过程中的内部协变量偏移(Internal Covariate Shift)问题,从而加速训练过程并提高模型的稳定性和性能。内部协变量偏移是指由于网络参数在训练过程中的变化,导致每一层的输入分布也在不断变化,这会使得网络的训练变得困难。
在每⼀层输⼊之前,将数据进⾏ BN ,然后再送⼊后续⽹络中进⾏学习:

批标准化的工作原理
批标准化通过在每一层的输入上进行标准化处理,使得每一层的输入分布保持相对稳定。具体来说,批标准化包括以下步骤:
- 计算均值和方差:对于每个小批量(mini-batch)的数据,计算该层输入的均值和方差:

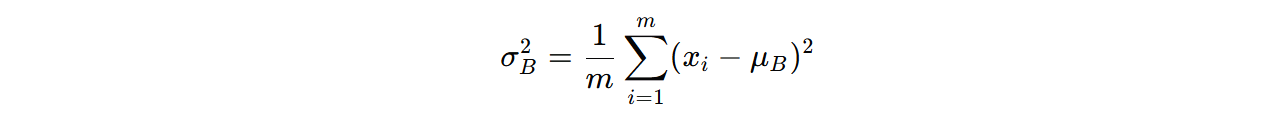
其中, m 是小批量的大小, xi 是第 i 个输入样本。
- 标准化:使用计算得到的均值和方差,对每个输入样本进行标准化:

其中, ϵ 是一个很小的常数,用于防止除以零的情况。
- 缩放和偏移:为了使网络具有足够的表达能力,引入两个可学习的参数 γ 和 β,对标准化后的输入进行缩放和偏移:
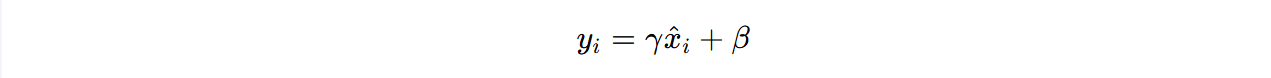
其中, γ 和 β 是通过训练学习得到的参数。
PyTorch中的实现在PyTorch中,批标准化可以通过torch.nn.BatchNorm1d、torch.nn.BatchNorm2d 和 torch.nn.BatchNorm3d 等类来实现,分别用于1D、2D和3D数据。
api
torch.nn.BatchNorm2d 是 PyTorch 中用于对二维卷积层输出进行 批量归一化(Batch Normalization)的模块。它通过规范化层的输入来 减少内部协变量偏移,从而加速训练过程并提高模型的泛化能力。
torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
| 参数名 | 解释 |
| num_features | 输入的通道数(num_channels),即输入张量的第二个维度。 |
| eps | 一个数值稳定性的小常数,用于防止除以零。默认值为 1e-5。 |
| momentum | 用于更新运行时均值和方差的动量参数。默认值为 0.1。较大的 momentum 会使估计值更依赖于之前的统计信息。 |
| affine | 布尔值
|
| track_running_stats | 布尔值,如果为 True,则在训练过程中跟踪运行时的均值和方差,并在评估模式下使用这些统计量进行归一化。默认值为 True。 |
以下是一个使用torch.nn.BatchNorm2d 的示例:
import torch
import torch.nn as nn# 定义 BatchNorm2d 模块
bn = nn.BatchNorm2d(3) # 假设输入通道数为 3# 创建一个假的输入数据,形状为 [batch_size, num_channels, height, width]
input = torch.randn(4, 3, 10, 10)# 应用 BatchNorm2d 模块
output = bn(input)
print(output.shape) # 输出形状与输入相同import torch
import torch.nn as nn# affine参数设为True表示weight和bias将被使用
m = nn.BatchNorm2d(2, eps=1e-05, momentum=0.1, affine=True)
"""
2:表示输入张量的通道数为2。
eps=1e-05:一个小的常数,用于防止除以零的情况。
momentum=0.1:用于计算运行时均值和方差的动量值。
affine=True:表示会使用可学习的权重和偏置参数。
"""
# 创建一个形状为 (1, 2, 3, 4) 的随机张量,表示一个批量大小为1,通道数为2,高度为3,宽度为4的输入数据。
input = torch.randn(1, 2, 3, 4)
print("input-->", input)
output = m(input)
print("output-->", output)
print(output.size())
print(m.weight)
print(m.bias)
"""
input--> tensor([[[[-0.8234, -1.2278, -0.4963, -2.3977],[-0.8070, 0.2189, -1.0539, 0.0155],[-2.8108, -2.0466, 0.3954, -0.0352]],[[-0.5503, -2.3331, -1.0138, -0.7310],[-1.2487, 0.2061, -1.0572, 0.0954],[ 0.5301, -0.3816, 0.1127, 0.0587]]]])
output--> tensor([[[[ 0.0989, -0.3051, 0.4256, -1.4736],[ 0.1153, 1.1400, -0.1314, 0.9369],[-1.8862, -1.1229, 1.3163, 0.8862]],[[-0.0314, -2.3395, -0.6315, -0.2653],[-0.9356, 0.9479, -0.6877, 0.8046],[ 1.3674, 0.1870, 0.8270, 0.7571]]]],grad_fn=<NativeBatchNormBackward0>)
torch.Size([1, 2, 3, 4])
Parameter containing:
tensor([1., 1.], requires_grad=True)
Parameter containing:
tensor([0., 0.], requires_grad=True)
"""批标准化层的权重和偏置参数默认初始化为1和0,但可以根据需要进行自定义初始化。
import torch
import torch.nn as nn# 创建一个卷积层
conv_layer = nn.Conv2d(in_channels=3, out_channels=16, kernel_size=3, padding=1)# 创建一个批标准化层
bn_layer = nn.BatchNorm2d(num_features=16)# 创建一个激活函数层
activation_layer = nn.ReLU()# 创建一个输入张量,假设是一个小批量的图像数据
input_tensor = torch.randn(4, 3, 32, 32) # (batch_size, channels, height, width)# 前向传播
conv_output = conv_layer(input_tensor)
bn_output = bn_layer(conv_output)
activated_output = activation_layer(bn_output)print("卷积层输出的形状:", conv_output.shape)
print("批标准化层输出的形状:", bn_output.shape)
print("激活函数层输出的形状:", activated_output.shape)批标准化的优点
- 加速训练:批标准化可以减少内部协变量偏移,使得每一层的输入分布保持相对稳定,从而加速训练过程。
- 提高模型性能:批标准化可以提高模型的稳定性和性能,尤其是在使用较深的网络时。
- 减少对初始化的依赖:批标准化可以减少对初始权重的依赖,使得模型对初始权重的选择更加鲁棒。
- 允许使用更高的学习率:由于批标准化可以减少梯度爆炸和梯度消失的问题,因此可以使用更高的学习率进行训练。
批标准化的注意事项
- 小批量大小:批标准化依赖于小批量的统计数据,因此小批量的大小不能太小。如果小批量大小太小,计算得到的均值和方差可能会不够准确,从而影响批标准化的效果。
- 推理时的行为:在推理(inference)时,批标准化层会使用在训练过程中计算得到的全局均值和方差,而不是当前小批量的均值和方差。这是通过在训练过程中逐步更新全局均值和方差来实现的。
- 与Dropout的结合:批标准化和Dropout都是正则化技术,但它们的作用机制不同。在使用批标准化时,可以适当减少Dropout的比例,因为批标准化本身也具有一定的正则化效果。
总结
知道 L2 正则化与 L1 正则化的⽅法
在损失函数( cost function )中增加⼀个正则项,由于添加了这个正则化项,权重矩阵的值减⼩,因为它假定具有更⼩权重矩阵的神经⽹络导致更简单的模型
知道随机失活 droupout 的应⽤
在每个迭代过程中,随机选择某些节点,并且删除前向和后向连接知道提前停⽌的使⽤⽅法
当看到验证集的性能越来越差时或者性能不再提升,⽴即停⽌对该模型的训练
知道 BN 层的使⽤⽅法
利⽤⽹络训练时⼀个 mini-batch 的数据来计算该神经元 xi 的均值和⽅差 , 归⼀化后并重构,因⽽称为 Batch Normalization
