基于C++实现(控制台)交通咨询系统
交通咨询系统
实验目的及要求
- 图的存储表示及其基本操作实现。
- 最短路径算法。
- 系统功能:要求设计一个简易的交通咨询系统,可让用户咨询任意两个城市之间的最短距离、最低花费或最少时间等问题。
- 对于不同的咨询要求,输入咨询的内容。
- 用户界面的友好性:程序能提供菜单供用户选择以及相应的交互信息。
算法原理概述
图的基本结构
- 有向图。若E是有向边(弧)的有限集合时,则图G为有向图。弧是顶点的有序对,记为<v,w>,其中v,w是顶点,v称为弧尾,w称为弧头,<v,w>称为从顶点v到顶点w的弧。
- 无向图。若E是无向边(边)的有限集合时,则图G为无向图。边是顶点的无序对,记为(v,w)或(w,v),因为两者相等,其中v,w是顶点,顶点V,w互为邻接点。边(v,w)依附于顶点v,w,或者边(v,W)和顶点v,w相关联。
- 简单图。一个图G若满足:①不存在重复边;②不存在顶点到自身的边,则称图G为简单图。
- 多重图。若图G中某两个结点之间的边数多于一条,又允许顶点通过一条边和自己关联,则图G为多重图。
- 完全图(筒单完全图)。对于无向图,任意两个顶点之间都存在边。对于有向图,任意两个顶点之间都存在方向相反的两条弧。
- 子图。设有两个图G=(V,E)和G'=(V,E),若”是V的子集,且E'是E的子集,则称G'是G的子图。若有满足V(G)=V(G)的子图G,则称其为G的生成子图。
- 连通、连通图。
在无向图中,若从顶点v到顶点w有路径存在,则称v和w是连通的。
若图G中任意两个顶点都是连通的,则称图G是连通图。极小连通子图是既要保持图连通又要使得边数最少的子图。 - 生成树。连通图的生成树是包含图中全部顶点的一个极小连通子图。
- 顶点的度、入度和出度。
对于无向图,顶点v是依附于该顶点的边的条数。无向图的全部顶点的度的和等于边数的两倍。
对于有向图,入度是以顶点v为终点的有向边的数目。出度是以顶点v为起点的有向边的数目。顶点的度等于入度和出度之和。有向图的全部顶点的入度之和与出度之和相等,并且等于边数。 - 边的权和网。在一个图中,每条边都可以标上具有某种意义的数值,该数值称为该边的权值。这种边上带有权值的图称为带权图,也称网。
图的存储结构
图的存储结构有四种:邻接矩阵法、邻接表法、十字链表法、邻接多重表法。(11)路径、路径长度和回路。
顶点v。到顶点v,之间的一条路径是指顶点序列Ve,V1,Ve…,Vm,Ve。
路径上边的数目称为路径长度。第一个顶点和最后一个顶点相同的路径称为回路或环。
图的存储结构
图的存储结构有四种:邻接矩阵法、邻接表法、十字链表法、邻接多重表法。
图的遍历
图的遍历是指从图中的某一顶点出发,按照某种搜索方法沿着图中的边对图中的所有顶点访问一次且仅访问一次。
图的遍历算法主要有两种:广度优先搜索和深度优先搜索。
最小生成树
对一个带权连通无向图,所有生成树中权值之和最小的生成树称为最小生成树。
最小生成树具有如下性质:
- 最小生成树不一定是唯一的,即最小生成树的树形不唯一。当带权连通无向图中的各边权值互不相等时,这时最小生成树才是唯一的。
- 最小生成树的边的权值之和总是唯一的。
- 最小生成树的边数为顶点数减1。
Prim算法求最小生成树:
①任取一顶点(或题中已告知顶点),去掉所有边
②选择一个与当前顶点集合距离最近的顶点,并将该顶点和相应的边加入进来,同时不形成回路
③重复②,直至图中所有顶点都并入。
下面给出Prim算法的C++实现
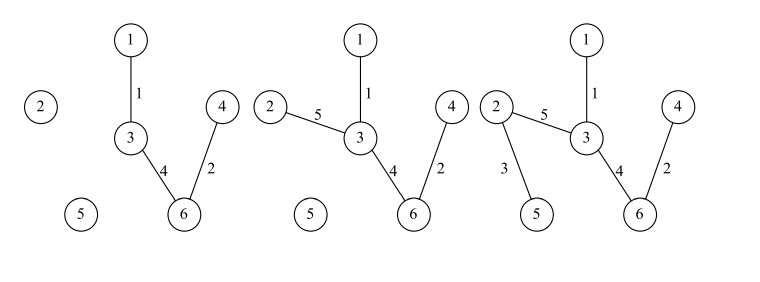
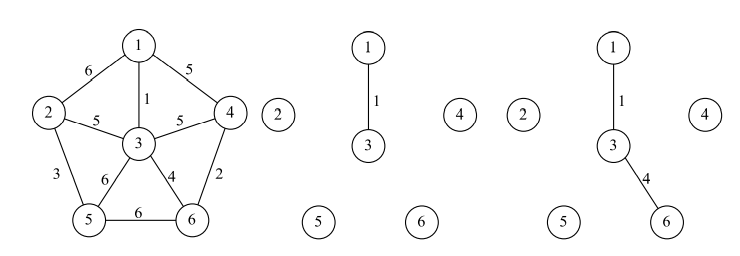
int prim(int cur){int index = cur;int sum = 0; //最短路径长 int i = 0 , j = 0;cout << index << "->";memset(visit,false, sizeof(visit));visit[cur] = true;for(i = 0; i < N; i++)lowcost[i] = map[cur][i];//初始化,将cur结点所有相连的边放入 for(i = 1; i < N; i++)//两重for循环 遍历每一个结点{int min= INF; //定义一个变量min初始化为一个极大值 //第一个for循环 未访问的点与与索引点index的比较for(j = 0; j < N; j++){if(!visit[j] && lowcost[j] < min)//找到未访问的点中,距离当前最小生成树距离最小的点{min = lowcost[j]; //不断更新与点cur的相连点的最短距离,将lowcost[j]权值更新数据到min上 更新权值 index = j;//将j数组下标更新到index中(即cur)更新结点 }}visit[index] = true;//标记距离最短的结点已经被访问过cout << index << "->";//输出新结点 sum += min;//权值累加 //第二个for循环 从index结点开始遍历的图中的新结点map[index][j]与最小生成树中lowcost[j]旧结点之间的权值遍历比较 for(j = 0; j < N; j++){if(!visit[j] && lowcost[j]>map[index][j]){lowcost[j] = map[index][j];}}}cout << endl;return sum; //返回最小生成树的总路径值}最短路径
设图G=<V,E>(无向图或有向图),给定W:E→R,对于G的每一条边e,称W(e)
为边e的权,把这样的图称作带权图,记作G=<V,E,W>。当e=(u,v)(<u,v>)时,把W(e)记作W(u,v)。
设P是G中的一条通路,P中所有边的权之和称作P的长度,记作W(P)。类似地,可以定义为回路C的长度w(C)。
设带权图G=<V,E,W>(无向图和有向图),其中每一条边e的权W(e)为非负实数。Vu,vEV,当u和v连通(u可达v)时,称从u到v的最短路径,称其长度为从u到v的距离,记作d(u,v)。约定:d(u,v)=0;当u和v不连通(u不可达v)时,d(u,v)=+∞。
最短路径问题:给定带权图G=<V,E,W>及顶点u和v,其中每一条边e的权W(e)
为非负实数,求从u到v的最短路径。
迪杰斯特拉算法求最短路径:
算法思想:迪杰斯特拉最最朴素的思想就是按长度递增的次序产生最短路径。即每次对所有可见点的路径长度进行排序后,选择一条最短的路径,这条路径就是对应顶点到源点的最短路径。
①初始化。V为G中所有顶点集合,S={v}。D[x]表示从源点到x的已知路径,
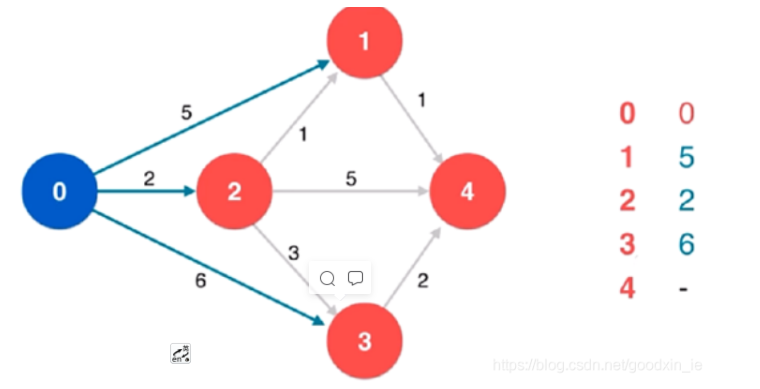
初始D[v]为0,其余为无穷大。
②从源点v开始运行一步广度优先算法即找其相邻点。如下图中从源点0开始,找到的可见点为1,2,3.
③计算可见点到源点v的路径长度,更新D[x]。然后对路径进行排序,选择最短的一条作为确定找到的最短路径,将其终点加入到S中,如此处找到的点为2,故将2加入S。S={v,2}.
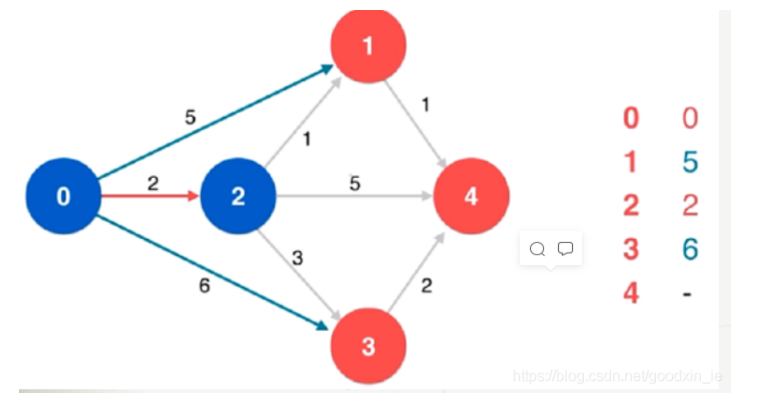
④从S中选择新加入的点运行广度优先算法找其相邻点,重复step3。直至所有点已加入S或者再搜索不到新的可见点(图中存在不联通的点,此时S<V)终止算法。
总结起来迪杰斯特拉算法总共就干了两件事:
【1】不断运行广度优先算法找可见点,计算可见点到源点的距离长度
【2】从当前已知的路径中选择长度最短的将其顶点加入S作为确定找到的最短路径的顶点。
C实现如下:
void LS(PGraph P, int v0, int D[], int Parent[]) //v0为源节点,数组D记录最小路径值
{int k, min;int n = 0;int result[6]; //记录已经访问的节点for (int i = 0; i < P->Nv; i++) //初始化 {result[i] = 0;D[i] = P->G[v0][i]; // 初始距离v0的距离if (P->G[v0][i] != INF)Parent[i] = v0; //初始存储的父节点集合}result[v0] = 1; //初始节点加入集合for (int i = 1; i < P->Nv; i++) //因为已经初始了与源节点相邻的节点,故只用遍历n-1次 {min = INF; //初始min为无穷大 for (int j = 0; j < P->Nv; j++){if (!result[j] && D[j] < min) //判断该节点没有被访问且存在新的最小距离{min = D[j]; //找出最小邻节点K k = j;}}result[k] = 1; //将新节点加入集合for (int j = 0; j < P->Nv; j++) //更新其余节点到源节点的值 {if (!result[j] && (min + P->G[k][j] < D[j])){Parent[j] = k;D[j] = min + P->G[k][j]; //更新距离}}}
}拓扑排序
AOV网:若用DAG图表示一个工程,其顶点表示活动,用有向边(V,V)表示活动”必须先于活动V,进行的这样一种关系,则将这种有向图称为顶点表示活动的网络,记为A0V网。
在AOV网中,活动是活动V的直接前驱,活动V是活动V,的直接后继,这种前驱和后继关系具有传递性,且任何活动V不能以它作为自己的前驱或后续。
在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,称为该图的一个拓扑排序:
①每个顶点出现且只出现一次。
②若存在一条从顶点A到顶点B的路径,则在排序中顶点B出现在顶点A的后面。
每个AOV网都有一个或多个拓扑排序序列。
拓扑排序的算法的步骤:
①从AOV网中选择一个没有前驱的顶点并输出。②从网中删除该顶点和所有以它为起点的有向边。
③重复①和②直到当前的AOV网为空或当前网中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。
软件开发环境及工具
计算机版本: Windows 10 专业版(H20)
处理器: Intel(R) Core(TM) i7-10750H CPU @2.60GHz
显卡: NVIDIA GeForce GTX 1650ti
机带:RAM 16.0 GB
开发软件:
CLion (2021.3) 专业版
运行时版本: 11.0.13+7-b1751.19 amd64
VM: OpenJDK 64-Bit Server VM,JetBrains s.r.o.
编译运行(控制台):
Target: i686-w64-mingw32
Thread model: posix
Supported LTO compression algorithms: zlib zstd
gcc version 10.2.0 (Rev6, Built by MSYS2 project)
GNU gdb (GDB) 9.2部分代码基于C++14标准,C基于C11标准进行开发调试
实验内容
问题提出:
设计一个交通咨询系统,可让用户咨询任意两个城市之间的最短距离、最低花费或最少时间等问题。
解决思路:
利用数据结构所学的图及其基本结构基于C/C++实现,其中图采用邻接表进行储存和表示, 使用Prim算法得到最下生成树,采用迪杰斯特拉算法求两点之间的最短路径,基于此基础进行实现。
选用邻接表易于查询某顶点的邻接点,边或弧的插入、删除但是在判定顶点是否邻接时,比邻接矩阵低效
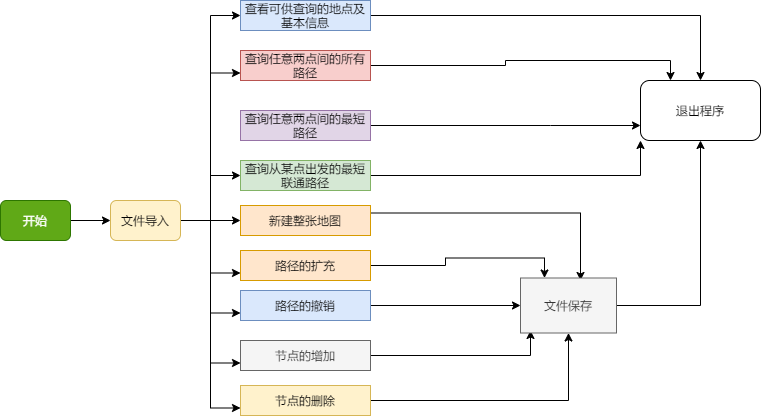
算法步骤:
声明结构体变量用于存储图及其相关结构
/**定义结构体类型存储弧结构*/
typedef struct node
{float distance; //距离int vexNode; //顶点struct node *next; //指向下一条弧的指针
} Arcnode;/**交通图节点元素类型*/
typedef struct vertexnode
{char name[30]; //地名char information[100]; //相应信息Arcnode *head; //下一个路径
} Line;/**图的存储结构定义*/
typedef struct adjlist
{Line point[M]; //顶点集合int arcnum; //顶点数int vexnum; //弧数
} map;/**队列结构体用于实现迪杰斯特拉算法*/
typedef struct quene
{int father;int son;struct quene *next;
} Quene;/**最小生成树节点定义:两点间最短路径*/
typedef struct mst_point
{int father;int son;struct mst_point *next;
} MST_point;核心模块:矩阵的初始化
/**初始化矩阵*/
void init_matrix(float (*matrix)[M])
{for (int i = 0; i < M; ++i){for (int j = 0; j < M; ++j){matrix[i][j] = INF;}}
}/**开辟空间存放地点名和地点信息*/
void init_map(map *g)
{for (auto &i: g->point){//void *memset(void *s,int c,size_t n)//总的作用:将已开辟内存空间 s 的首 n 个字节的值设为值 cmemset(i.name, 0, 30 * sizeof(char));memset(i.information, 0, 100 * sizeof(char));}for (auto &i: g->point){i.name[29] = '\n';i.information[29] = '\n';}
}链队列的初始化及出入对操作
/**初始化队列*/
Quene *init_Quene()
{auto *head = (Quene *) malloc(sizeof(Quene));head->next = nullptr;return head;
}
/**入队操作 插入元素,i:父亲节点 j:孩子节点*/
void push(Quene *head, int i, int j)
{auto *temp = (Quene *) malloc(sizeof(Quene));if (temp){temp->father = i;temp->son = j;temp->next = head->next;head->next = temp;}
}/**出队操作*/
void pop(Quene *head, int &i, int &j)
{Quene *temp;if (!isEmpty(head)){temp = head->next;i = temp->father;j = temp->son;head->next = temp->next;free(temp);}
}核心模块:地图的创建操作
/**地图的创建*/
void creat_map(map *g, float (*matrix)[M], FILE *fp)
{Arcnode *temp;int vexnum;int w;int vexnode;float distance;init_map(g);cout << "请输入要创建的节点(地点:下同)个数: " << endl;cin >> vexnum;fprintf(fp, "%d\n", vexnum);g->vexnum = vexnum;for (int i = 0; i < vexnum; ++i){g->point[i].head = (Arcnode *) malloc(sizeof(Arcnode));g->point[i].head->next = nullptr;printf("\n---正在创建第 %d/%d 个根节点---\n", i + 1, vexnum);printf("===>>>请输入第[%d]个根节点的名字:", i + 1);cin >> g->point[i].name;fwrite(g->point[i].name, 30, 1, fp);printf("===>>>请输入地点'%s'根的基本信息\n", g->point[i].name);cin >> g->point[i].information;fwrite(g->point[i].information, 100, 1, fp);printf("\n请问有多少节点连接到根节点'%s': ", g->point[i].name);cin >> w;fprintf(fp, "%d\n", w);//格式化保存至文件for (int j = 0; j < w; ++j){printf("**开始创建连接到'%s'的节点,当前: %d/%d 个节点**\n", g->point[i].name, j + 1, w);temp = (Arcnode *) malloc(sizeof(Arcnode));printf("请输入第%d个连接到 '%s' 的节点对应的数字编号===>>> ", j + 1, g->point[i].name);cin >> vexnode;printf("请输入该节点到 '%s' 的距离===>>> ", g->point[i].name);cin >> distance;fprintf(fp, "%d %f\n", vexnode, distance);temp->vexNode = vexnode;temp->distance = distance;temp->next = g->point[i].head->next;g->point[i].head->next = temp;matrix[i][vexnode] = distance;printf("\n地点(根节点):'%s'==>第%d个节点点创建成功!\n", g->point[i].name, j + 1);}printf("---创建第 %d个节点创建成功,名称:'%s',编号:%d!---\n", i + 1, g->point[i].name, i);cout << "//********************************************************//" << endl;system("pause");}
}核心模块:Prim算法求最小生成树
/**Prim算法获取最小生成树*/
MST_point *prim(map *g, float(*matrix)[M], int start)
{ auto *head = (MST_point *) malloc(sizeof(MST_point)); MST_point *temp; struct { int adjvex; int lowcost; } closedge[M]; int s, min; head->next = nullptr; closedge[start].lowcost = 0; for (int i = 0; i < g->vexnum; ++i) { if (i != start) { closedge[i].adjvex = start; closedge[i].lowcost = matrix[start][i]; } } for (int i = 0; i < g->vexnum - 1; ++i) { min = INF; for (int j = 0; j < g->vexnum; ++j) { if (closedge[j].lowcost != 0 && closedge[j].lowcost < min) { s = j; min = closedge[j].lowcost; } } temp = (MST_point *) malloc(sizeof(MST_point)); temp->father = closedge[s].adjvex; temp->son = s; temp->next = head->next; head->next = temp; closedge[s].lowcost = 0; for (int j = 0; j < g->vexnum; ++j) { if (j != s && matrix[s][j] < closedge[j].lowcost) { closedge[j].lowcost = matrix[s][j]; closedge[j].adjvex = s; } } } return head;
}核心模块:迪杰斯特拉算法求两点间最短路径
void dijkstra(map *g, float (*matrix)[M], int start, int end, int dist[M], int path[M][M + 1])
{ cout << "正在调用dijkstra算法" << endl; int mindist; int t, k; for (int i = 0; i < g->vexnum; ++i) { path[i][0] = 0; } for (int i = 0; i < g->vexnum; ++i) { for (int j = 1; j < M + 1; ++j) { path[i][j] = -1; } } for (int i = 0; i < g->vexnum; ++i) { dist[i] = matrix[start][i]; if (matrix[start][i] != INF) { path[i][1] = start; } } path[start][0] = 1; for (int i = 1; i < g->vexnum; ++i) { mindist = INF; for (int j = 0; j < g->vexnum; ++j) { if (!path[j][0] && dist[j] < mindist) { k = j; mindist = dist[j]; } } if (mindist == INF) { printf("暂且未查询这两点间路径!\n"); return; } path[k][0] = 1; for (int j = 1; j < M; ++j) { if (!path[j][0] && matrix[k][j] < INF && (dist[k] + matrix[k][j] < dist[j])) { dist[j] = dist[k] + matrix[k][j]; t = 1; while (path[k][t] != -1) { path[j][t] = path[k][t]; t++; } path[j][t] = k; } } } printf("%s 与 %s 之间的最短路径为: \n", g->point[start].name, g->point[end].name); t = 1; while ((k = path[end][t]) != -1) { printf("%s ->", g->point[k].name); t++; } printf("%s\n", g->point[end].name); printf("\n距离为: %d\n", dist[end]);
}主函数功能实现
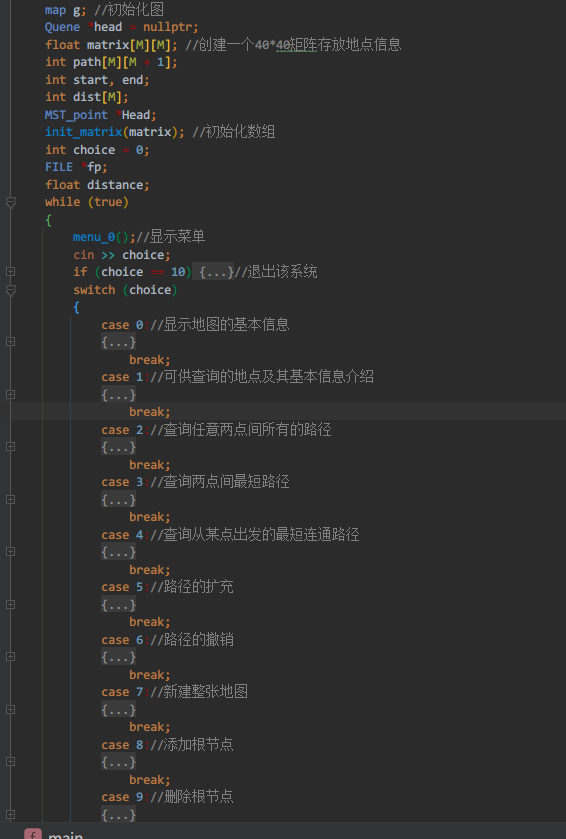
结果分析:
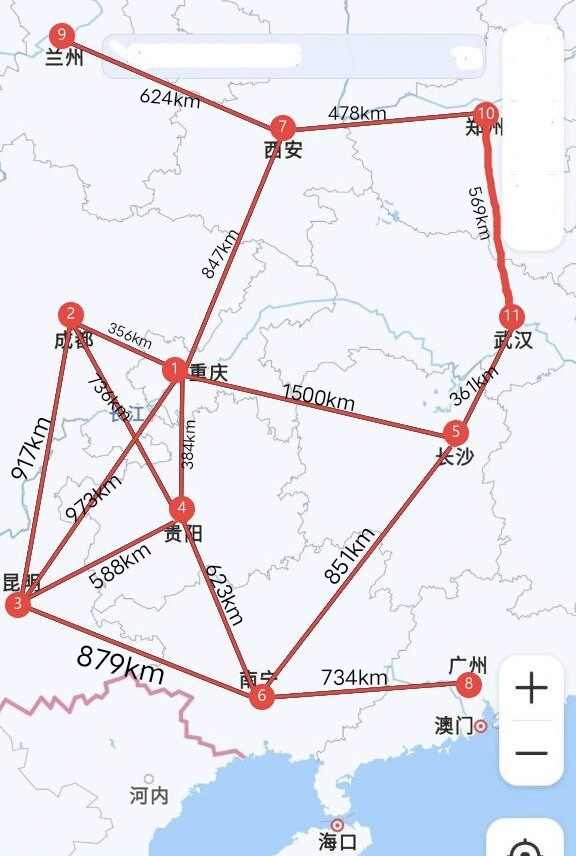
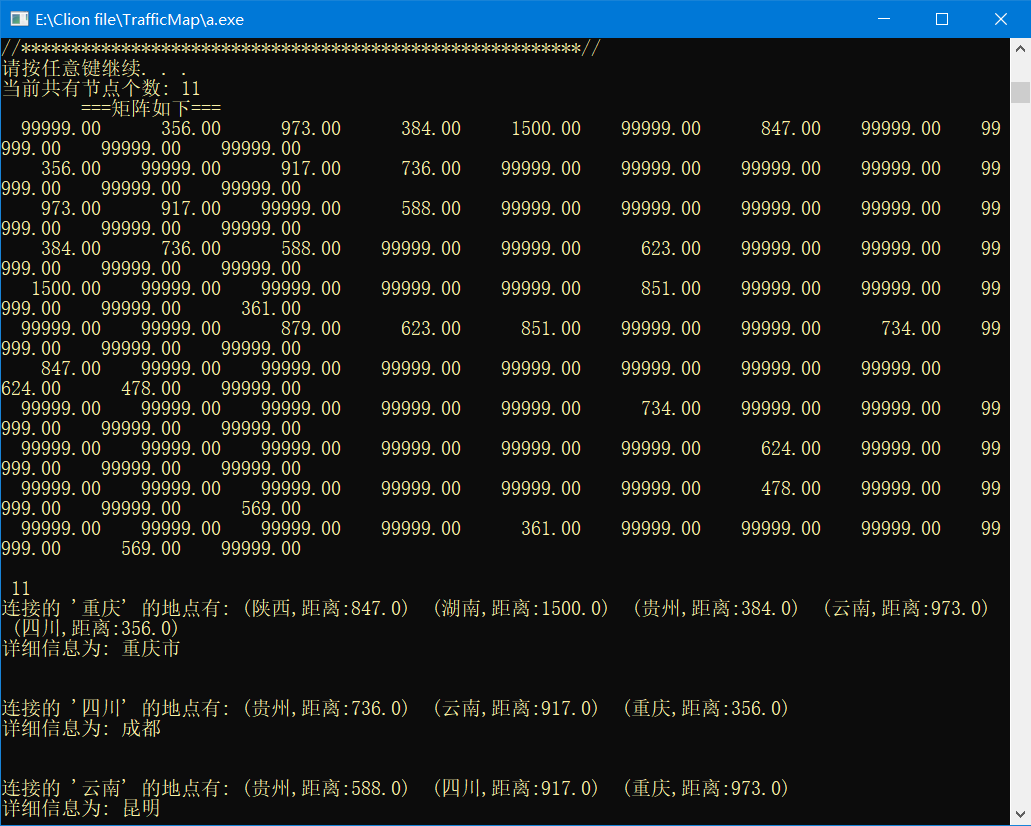
本程序所存储的地图信息如下:
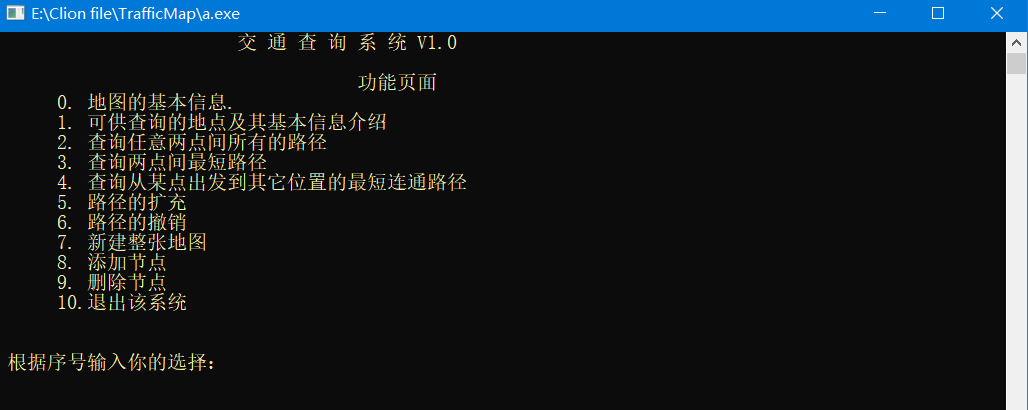
开始菜单界面

新建整张地图,这里由于时间有限,没能全部录入中国的省份信息,仅以重庆为中心录入了周围相邻省份
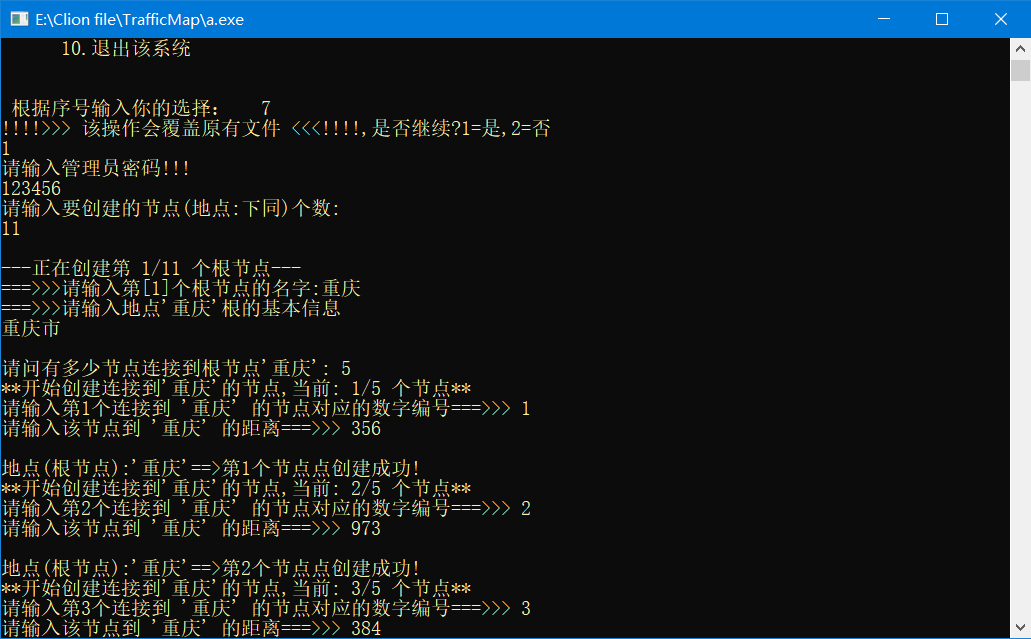
显示地图基本信息
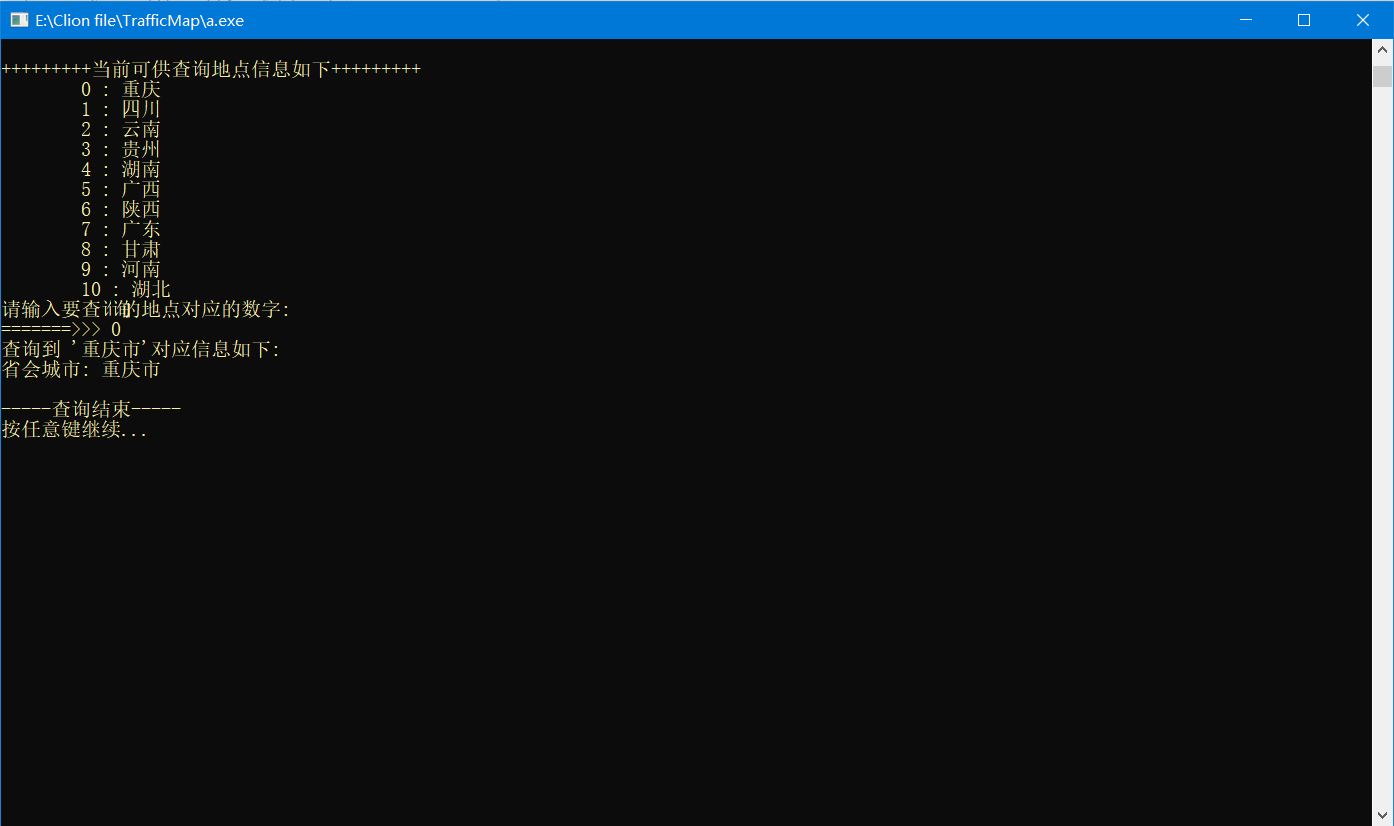
查看某地点详细信息
任意两点之间的所有路径
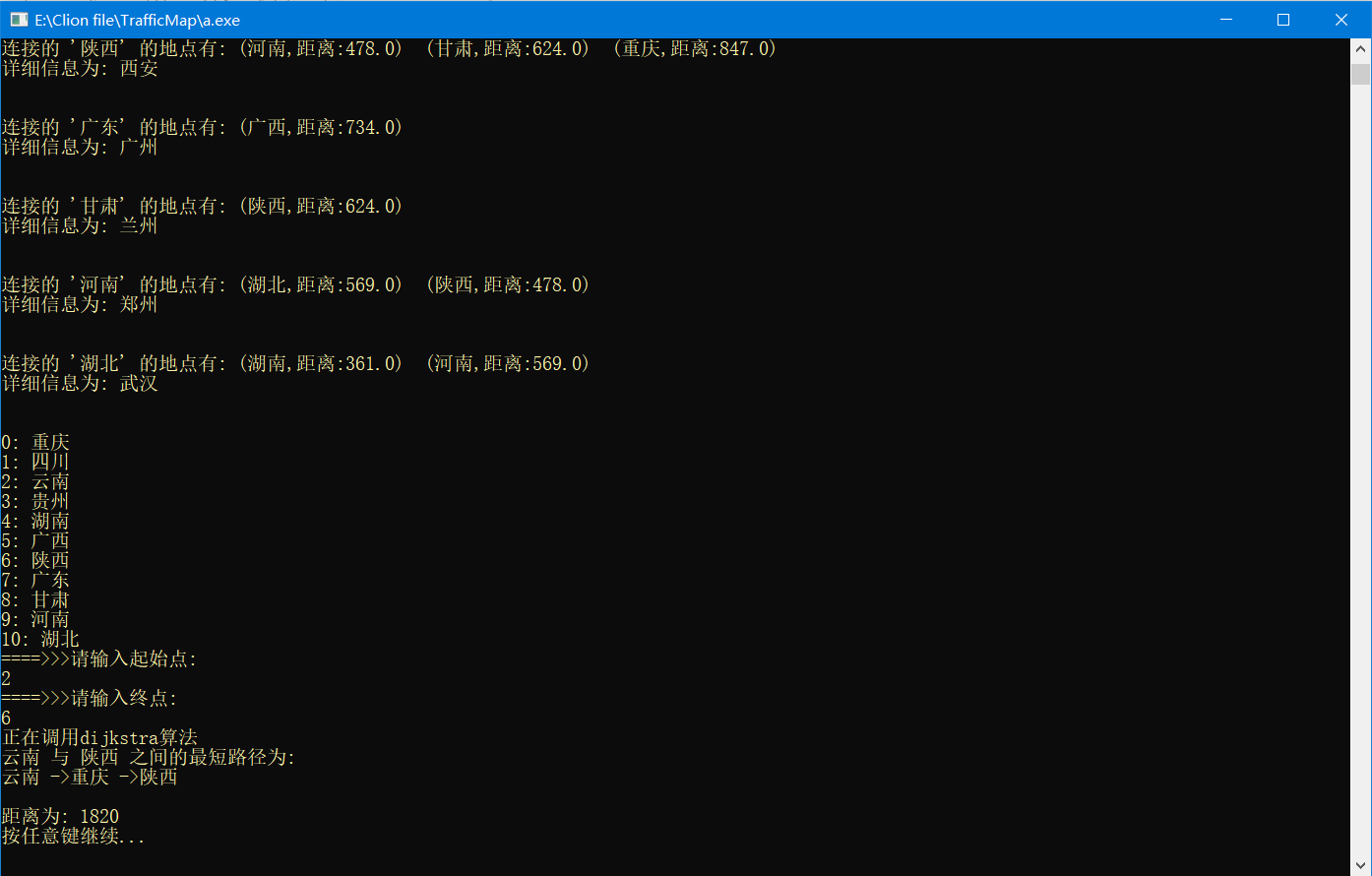
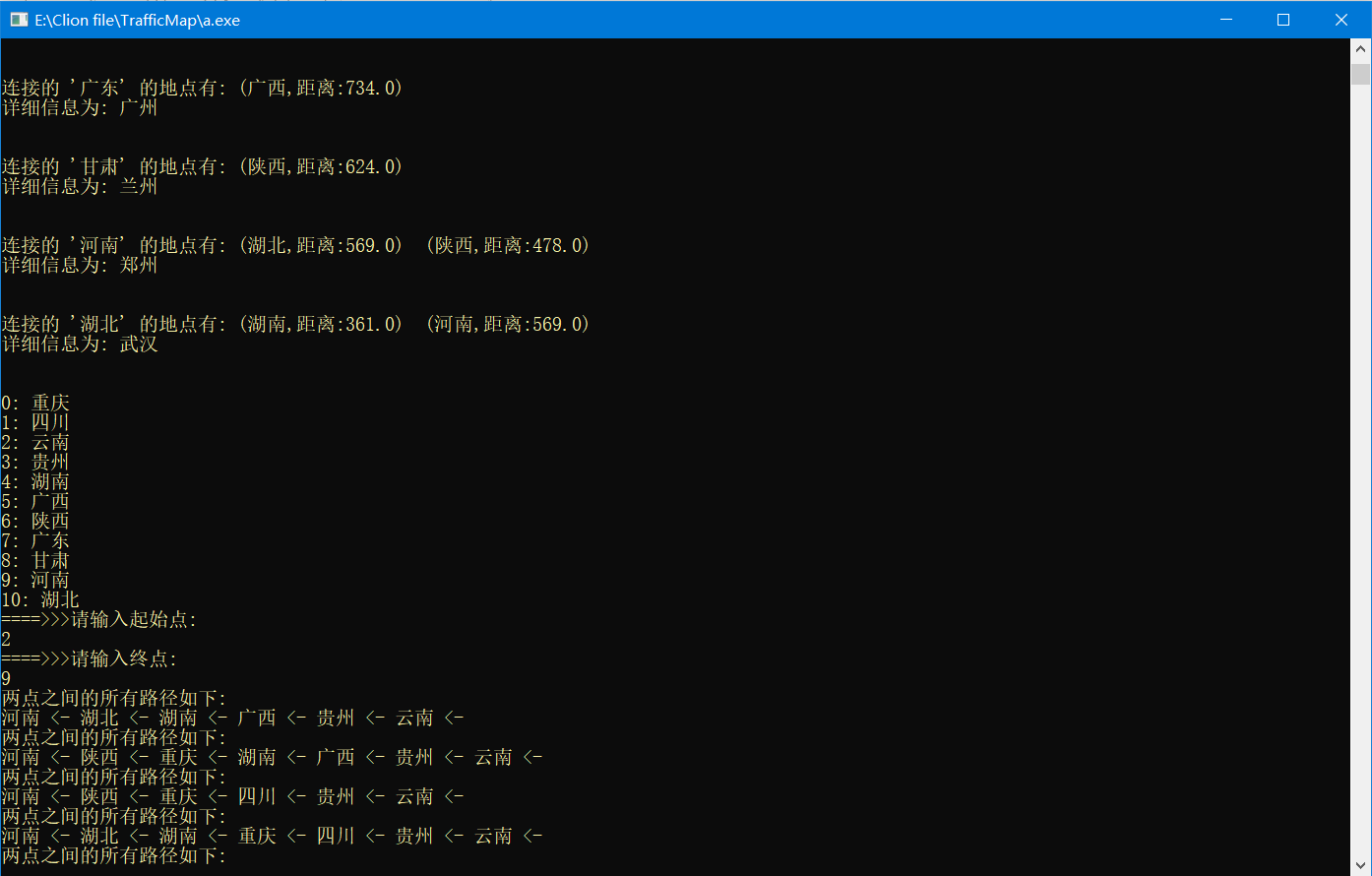
查询从某点出发到其它位置的最短连通路径
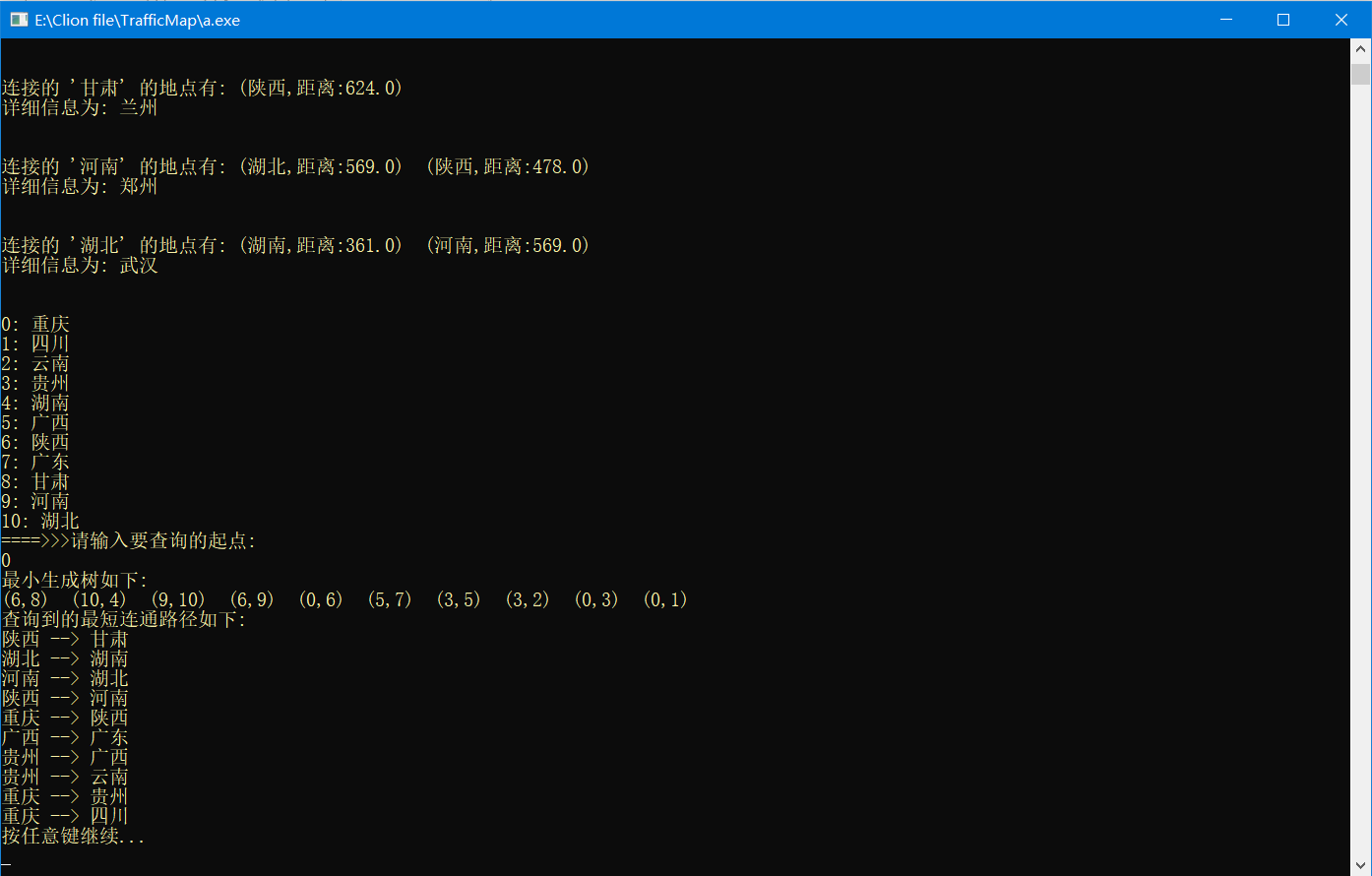
查看任意两点之间的最短路径
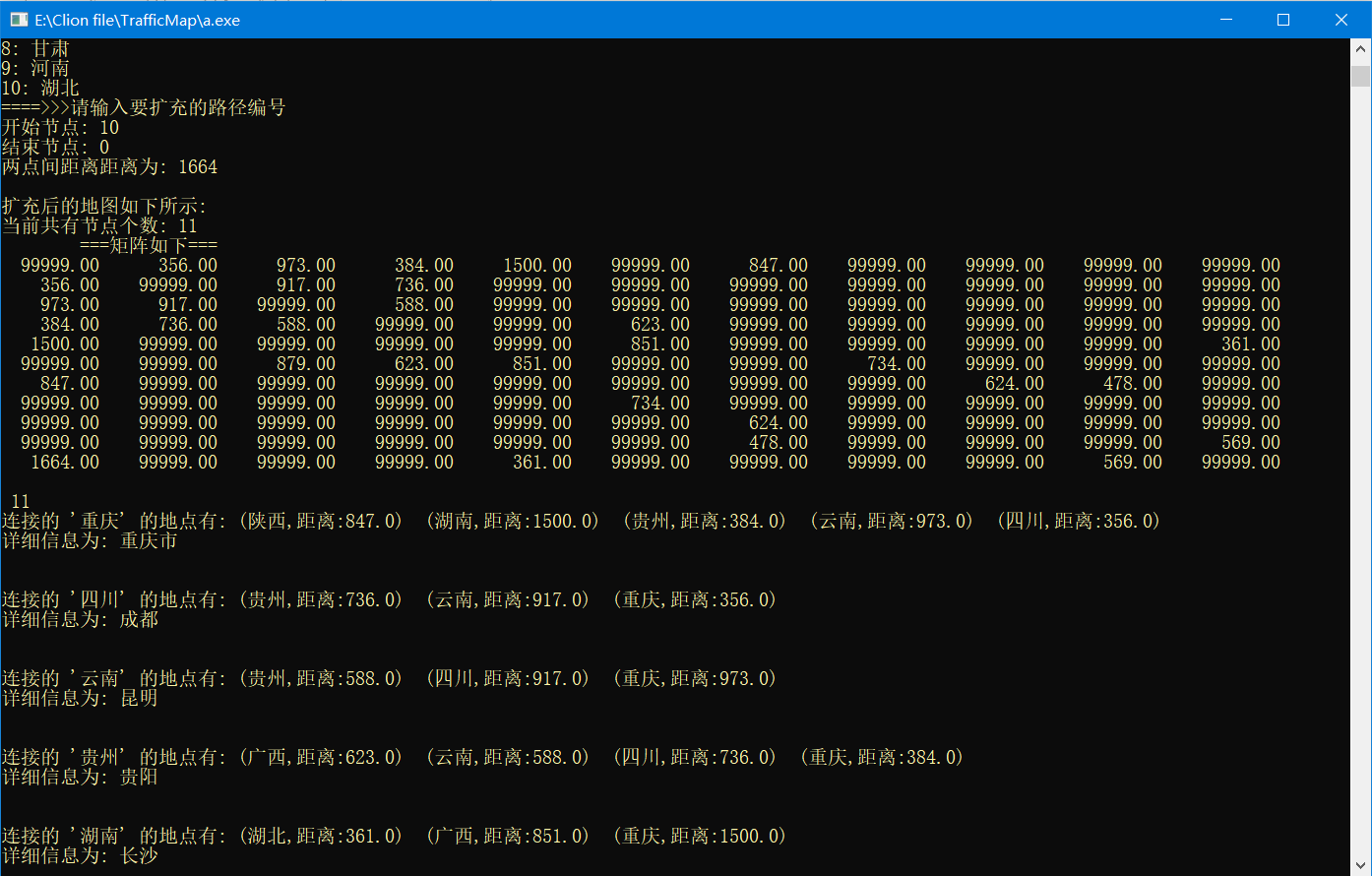
路径扩充
实验总结
通过本次课程设计,对图的概念有了一个新的认识,在学习离散数学的时候,总觉得图是很抽象的东西,但是在学习了《数据结构》这门课程之后,我慢慢地体会到了其中的奥妙,图能够在计算机中存在,首先要捕捉他有哪些具体化、数字化的信息,比如说权值、顶点个数等,这也就说明了想要把生活中的信息转化到计算机中必须用数字来完整的构成一个信息库,而图的存在,又涉及到了顶点之间的联系。图分为有向图和无向图,而无向图又是有向图在权值双向相等下的一种特例,如何能在计算机中表示一个双向权值不同的图,这就是一件很巧妙的事情,经过了思考和老师同学的帮助,我用邻接表就能实现了一个双向图信息的存储。对整个程序而言,dijkstra 算法始终都是核心内容,其实这个算法在实际思考中并不难,也许我们谁都知道找一个路径最短的方法,及从顶点一步一步找最近的路线并与其直接距离相比较,但是,在计算机中实现这么一个很简单的想法就需要涉及到很多专业知识,为了完成设计,在前期工作中,基本都是以复习C/C++为主,所以浪费了很多时间,比如说在程序中,删除顶点和增加顶点的模块中都有和建图模块相互重复的函数,但是由于技术的原因,只能做一些很累赘的函数,可见在调用知识点,我没有掌握好。这也让我认识到数据结构是一门比较难的课程,需要多花时间上机练习。不过,有了这次课程设计的经验和教训,我能够很清楚的对自己定一个合适的水平。因为课程设计的题目是求最短路径,本来是想通过算法的实现把这个程序与交通情况相连,但是因为来不及查找各地的信息,所以,这个计划就没有实现,我相信在以后有更长时间的情况下,能够对其进行实现。同时,在老师和同学的帮助之下,这次的程序训练培养了我实际分析问题、编程和动手能力,使我又掌握了一些程序设计的基本技能,提高了我适应实际,实践编程的能力。
