当前位置：首页 > ops >正文

算法面试题（上）

ops 2025/9/2 5:59:20

1. 多线程

概念：多线程是指在同一进程内并发执行多个线程，每个线程共享进程的内存空间和资源，但有独立的栈。
优点：
- 提高 CPU 利用率（特别是 I/O 密集型任务）。
- 能在一个进程内并行处理多个任务。
缺点：
- 编程复杂（需要处理同步、死锁、竞态条件）。
- 上下文切换有开销。
常用同步方式：互斥锁（std::mutex）、读写锁、条件变量、原子操作（std::atomic）。
C++ 支持：

C++11 引入 std::thread、std::mutex、 std::condition_variable、std::future 等。

#include <iostream>
#include <thread>
#include <mutex>using namespace std;mutex mtx; // 全局互斥锁void printTask(int id) {  lock_guard<mutex> lock(mtx); // 自动加锁/解锁cout << "Thread " << id << " is running\n";
}int main() {thread t1(printTask, 1);thread t2(printTask, 2);t1.join();t2.join();return 0;
}

2. STL 有什么？

STL（Standard Template Library）主要包括六大组件：

1. 容器：vector、list、deque、set、map、unordered_map 等。2. 算法：sort、find、for_each、binary_search 等。3. 迭代器：连接算法与容器的“胶水”，如 begin()、end()。4. 函数对象（仿函数）：可调用对象，如 greater<int>。5. 适配器：对容器、迭代器或函数对象进行改造，例如 stack（基于 deque）、priority_queue、function。6. 分配器：内存分配与回收机制，默认 std::allocator。

3. vector 扩充方式，size 与 capacity 区别

扩充方式：
- 当 size == capacity 时，再插入元素会触发扩容。
- C++ 标准没规定倍数，但多数实现是按 2 倍增长（如 GCC 的 libstdc++）。
- 扩容会重新分配更大内存，并拷贝（或移动）旧元素过去。
区别：
- size()：当前已存储的元素个数。
- capacity()：已分配内存可容纳的最大元素数（不必重新分配）。
- reserve(n)：预分配至少 n 的容量（减少扩容次数）。

4. 顺序存储结构有哪些？

顺序存储结构是用一段连续的内存存储数据元素的结构：

线性结构：
- 顺序表（如 std::vector、数组）。
- 栈（顺序栈）。
- 队列（顺序队列）。
非线性结构（少见，但可以顺序存储）：
- 完全二叉树（用数组存储，如堆）。
- 邻接矩阵（存储图）。
- 哈希表（开地址法）。

5. 左值引用与右值引用

左值引用（T&）：
- 绑定到有名字的对象，可读可写。
- 用于传递大对象避免拷贝。

例：

int x = 10;
int& ref = x; // 左值引用

右值引用（T&&）：
- 绑定到临时对象（右值），允许对临时对象修改。
- 常用于移动语义（减少拷贝）和完美转发。

例：

int&& rref = 10; // 绑定临时值
std::vector<int> v1, v2;
v1 = std::move(v2); // 移动语义

本质：
- 左值：有持久地址的对象。
- 右值：表达式求值结果，不再被使用的临时值。
- std::move() 并不移动，只是把左值强制转为右值引用。

6. 虚函数与纯虚函数

1. 虚函数 (Virtual Function)

定义：有具体实现的函数
语法：virtual void func() { /* 实现 */ }
特点：
基类可以提供默认实现
派生类可以选择重载或不重载
基类可以实例化
2. 纯虚函数 (Pure Virtual Function)
定义：没有实现的抽象函数
语法：virtual void func() = 0;
特点：
基类不提供实现
派生类必须重载实现
基类不能实例化（抽象类）

#include <iostream>
using namespace std;// 抽象基类 - 包含纯虚函数
class Shape {
public:virtual double getArea() = 0;        // 纯虚函数virtual void draw() = 0;             // 纯虚函数virtual void printInfo() {           // 虚函数（有默认实现）cout << "这是一个图形\n";}
};// 派生类1
class Circle : public Shape {
private:double radius;
public:Circle(double r) : radius(r) {}double getArea() override {return 3.14159 * radius * radius;}void draw() override {cout << "绘制圆形，半径: " << radius << endl;}void printInfo() override {  // 可以选择重载虚函数cout << "这是一个圆形，半径: " << radius << endl;}
};// 派生类2
class Rectangle : public Shape {
private:double width, height;
public:Rectangle(double w, double h) : width(w), height(h) {}double getArea() override {return width * height;}void draw() override {cout << "绘制矩形，宽: " << width << "，高: " << height << endl;}// 不重载printInfo()，使用基类的默认实现
};int main() {// Shape s; // 错误！抽象类不能实例化Circle c(5);Rectangle r(4, 6);// 多态调用Shape* shapes[] = {&c, &r};// 基类指针数组，存储派生类对象的地址for (Shape* shape : shapes) { // 根据实际对象类型调用相应的方法shape->printInfo();  // 虚函数调用shape->draw();       // 纯虚函数调用cout << "面积: " << shape->getArea() << endl; // 纯虚函数调用cout << "---" << endl;}return 0;
}

7. 手撕memcpy 、memset

#include <stddef.h>void *my_memcpy(void *dst, const void *src, size_t n) {// 注意：src/dst 重叠时行为未定义，应该用 memmoveunsigned char *d = (unsigned char *)dst;const unsigned char *s = (const unsigned char *)src;while (n--) *d++ = *s++;return dst;
}void *my_memset(void *s, int c, size_t n) {unsigned char *p = (unsigned char *)s;unsigned char v = (unsigned char)c;while (n--) *p++ = v;return s;
}

++ 的优先级高于*，所以*p++ = *（p++）

8. 一行代码求平方根

double r = exp(0.5 * log(x));  // 需 #include <math.h>

double r = std::pow(x, 0.5);   // 需 <cmath>

9. 排序方法对比

排序算法	平均时间复杂度	最坏时间复杂度	最好时间复杂度	空间复杂度	稳定性
快速排序	O(n log n)	O(n²)	O(n log n)	O(log n)（递归栈）	❌ 不稳定
归并排序	O(n log n)	O(n log n)	O(n log n)	O(n)	✅ 稳定
堆排序	O(n log n)	O(n log n)	O(n log n)	O(1)	❌ 不稳定
桶排序	O(n + k)	O(n + k)	O(n + k)	O(n + k)	✅ 稳定（若桶内用稳定算法）

桶排序依赖输入分布，k 是桶数（范围大小），适合数据范围有限 & 分布均匀的情况。

1️⃣ 快速排序 (QuickSort)

void quicksort(vector<int>& a, int l, int r) {if (l >= r) return;int i = l, j = r, pivot = a[l]; // 取左端点为枢轴while (i < j) {while (i < j && a[j] >= pivot) j--;if (i < j) a[i++] = a[j];while (i < j && a[i] <= pivot) i++;if (i < j) a[j--] = a[i];}a[i] = pivot;quicksort(a, l, i - 1);quicksort(a, i + 1, r);
}

把小的放左边，大的放右边，再递归排序两边

2️⃣ 归并排序 (MergeSort)

void merge(vector<int>& a, int l, int mid, int r) {vector<int> tmp(r - l + 1);int i = l, j = mid + 1, k = 0;while (i <= mid && j <= r) {tmp[k++] = (a[i] <= a[j]) ? a[i++] : a[j++];}while (i <= mid) tmp[k++] = a[i++];while (j <= r) tmp[k++] = a[j++];for (int t = 0; t < tmp.size(); t++) a[l + t] = tmp[t];
}void mergesort(vector<int>& a, int l, int r) {if (l >= r) return;int mid = (l + r) / 2;mergesort(a, l, mid);mergesort(a, mid + 1, r);merge(a, l, mid, r);
}

👉 分而治之：把数组分成两半，分别排序，再合并两个有序数组。

原理：

递归拆分数组，直到区间只剩一个元素（天然有序）。

合并两个有序子数组成一个有序数组（像“拉拉链”一样左右比较）。

特点：

稳定（相等元素相对顺序不变）。

时间复杂度稳定 O(n log n)。

缺点是需要 O(n) 的辅助数组空间。

3️⃣ 堆排序 (HeapSort)

void heapify(vector<int>& a, int n, int i) {int largest = i, l = 2*i+1, r = 2*i+2;if (l < n && a[l] > a[largest]) largest = l;if (r < n && a[r] > a[largest]) largest = r;if (largest != i) {swap(a[i], a[largest]);heapify(a, n, largest);}
}void heapsort(vector<int>& a) {int n = a.size();// 建堆for (int i = n/2 - 1; i >= 0; i--) heapify(a, n, i);// 取堆顶元素（最大值），放到数组末尾for (int i = n-1; i > 0; i--) {swap(a[0], a[i]);heapify(a, i, 0);}
}

👉 利用堆这种数据结构（最大堆/最小堆），不断取堆顶元素。

原理：

把数组“堆化”（建成一个大顶堆：每个父节点 ≥ 子节点）。

堆顶就是最大值，把它放到数组末尾（交换堆顶和末尾元素）。

把堆的大小减 1，再调整堆，继续取最大值。

重复，直到数组有序。

特点：

不稳定（堆调整时可能打乱相等元素顺序）。

时间复杂度稳定 O(n log n)，不怕最坏情况。

空间复杂度 O(1)，因为原地堆化。

4️⃣ 桶排序 (BucketSort)

适合范围较小（例如 0 ~ 10000）的整数。
这里给个最简版：

void bucketsort(vector<int>& a, int maxVal) {vector<int> bucket(maxVal+1, 0);for (int x : a) bucket[x]++;int idx = 0;for (int i = 0; i <= maxVal; i++) {while (bucket[i]--) a[idx++] = i;}
}

👉 把数据按范围分到不同“桶”里，再对每个桶内部排序，最后依次合并。

原理：

假设数的范围已知（比如 0~100）。

创建若干个桶，把元素分配到对应桶里。

桶内可以直接放链表（保持稳定），或者再用快排/插排。

最后按桶的顺序依次输出。

特点：

时间复杂度接近 O(n)（当数据分布均匀时）。

稳定（如果桶内用稳定排序）。

但需要额外空间，且不适合范围特别大但数据稀疏的场景。

（计数排序、基数排序其实都是“桶思想”的特例）
上面是“计数排序”版桶排。更一般的桶排序会用vector<vector> 来放桶，每个桶内部再排序。

⚡ 总结：

快排平均最快，但最坏 O(n²)；工程上常用“三数取中”或随机化 pivot 来避免退化。

归并排序稳定，但需要 O(n) 额外空间；适合链表。

堆排序空间最优 O(1)，但常数比快排大，实际一般比快排慢。

桶排序线性时间，但依赖数据分布；适合整数范围小的场景。

“快排快，归并稳，堆排省空间，桶排看分布”

⚡️ 直观对比口诀

快排：选枢轴，左右分治，小的左，大的右。

归并：拆到最小，合并有序，像“拉拉链”。

堆排：建大顶堆，堆顶最大，换到末尾。

桶排：按范围分桶，桶内再排，最后合并。

10. 二叉树排序、堆排序、希尔排序、桶排序时间复杂度

算法	最好时间复杂度	平均时间复杂度	最坏时间复杂度	空间复杂度	稳定性
二叉树排序（Binary Tree Sort）	O(n log n)	O(n log n)	O(n²)（退化成链表时）	O(n)（建树需要指针存储）	取决于树的实现（普通二叉查找树不稳定，平衡树可稳定）
堆排序（Heap Sort）	O(n log n)	O(n log n)	O(n log n)	O(1)（原地排序）	❌ 不稳定
希尔排序（Shell Sort）	O(n log n) ~ O(n^1.3)（取决于增量序列）	O(n log² n) 或更优	O(n²)	O(1)	❌ 不稳定
桶排序（Bucket Sort）	O(n + k)（k = 桶数）	O(n + k)	O(n²)（数据分布极不均匀）	O(n + k)	✅ 稳定（如果桶内用稳定排序）

📌 核心解释

二叉树排序

把所有元素依次插入二叉查找树，再做一次中序遍历 → 得到有序序列。

如果树平衡（如 AVL 树 / 红黑树），时间复杂度 O(n log n)。

如果树退化成链表（比如插入已经排好序的数据），时间复杂度 O(n²)。

堆排序

先建大顶堆（O(n)），再执行 n 次“交换堆顶 + 堆化”操作（O(log n)）。

整体 O(n log n)，稳定 O(1) 额外空间。

不稳定，因为堆化时可能会打乱相等元素的顺序。

希尔排序

希尔排序是插入排序的优化版：先按一定的 gap（步长）分组，再对分组做插入排序，逐步缩小 gap 直到 1。

时间复杂度依赖 gap 序列：

原始 Shell 增量：最坏 O(n²)

Hibbard 增量：O(n^1.5)

Sedgewick 增量：O(n^1.3)

空间复杂度 O(1)，但稳定性不好。

桶排序

把数据分到若干个“桶”里，每个桶内部再排序，最后合并桶。

如果数据分布均匀，复杂度接近 O(n)。

如果所有数据都挤在一个桶 → 退化为 O(n²)。

桶排序依赖输入数据的分布和范围，因此不适合比较型排序的通用场景。

✅ 总结一句话：

二叉树排序：依赖树是否平衡

堆排序：稳定 O(n log n)，但不稳定

希尔排序：插入排序的“加速版”，性能介于 O(n log² n) 和 O(n^1.3) 之间

桶排序：理论上最快 O(n)，但依赖数据分布

11. 树的DFS与BFS、树的遍历

🌳 一、DFS 和 BFS 是什么？

DFS（深度优先搜索，Depth First Search）

走到底再回头。

想象你在迷宫里走路：你总是往一个方向一直走，直到走不通，再回退，换另一条路。

在树里就是：先一路走到最深的子节点，再往上回来。

实现方式：递归或者用栈。

BFS（广度优先搜索，Breadth First Search）

一层一层地走。

想象你在看一棵大树：先看根，然后看根的所有孩子，再看孩子的孩子……一圈一圈往外扩散。

在树里就是：从上到下、从左到右逐层访问。

实现方式：用队列。

🌳 二、树的常见遍历方式

树的遍历就是按照某种规则，把树的所有节点走一遍。

二叉树的 DFS 遍历（3 种方式）

对一个二叉树节点 root：
A
/
B C
/
D E
前序遍历 (Preorder)：根 → 左 → 右
👉 顺序是：A → B → D → E → C

中序遍历 (Inorder)：左 → 根 → 右
👉 顺序是：D → B → E → A → C

后序遍历 (Postorder)：左 → 右 → 根
👉 顺序是：D → E → B → C → A

📌 可以记口诀：

前序：根在前

中序：根在中

后序：根在后

BFS 遍历（二叉树的层序遍历）

就是「从上到下，一层一层访问」。
对于上面那棵树：
👉 A → B → C → D → E

实现方法：用队列（先进先出）。

#include <iostream>
#include <queue>
using namespace std;struct TreeNode {char val;TreeNode *left, *right;TreeNode(char x): val(x), left(NULL), right(NULL) {}
};// 前序遍历 DFS
void preorder(TreeNode* root) {if (!root) return;cout << root->val << " ";preorder(root->left);preorder(root->right);
}// 中序遍历 DFS
void inorder(TreeNode* root) {if (!root) return;inorder(root->left);cout << root->val << " ";inorder(root->right);
}// 后序遍历 DFS
void postorder(TreeNode* root) {if (!root) return;postorder(root->left);postorder(root->right);cout << root->val << " ";
}// 层序遍历 BFS
void levelorder(TreeNode* root) {if (!root) return;queue<TreeNode*> q;q.push(root);while (!q.empty()) {TreeNode* node = q.front();q.pop();cout << node->val << " ";if (node->left) q.push(node->left);if (node->right) q.push(node->right);}
}

12. 对于n个实例的k维数据，建立kd tree的时间复杂度

🌟 kd-tree 的构建过程

对于 n 个 k 维点：

选取划分维度

常见做法是每层选取一个维度（比如轮流选），或者选方差最大的维度。

这个操作复杂度 ≈ O(k)（维度数通常远小于 n，可以近似忽略不计）。

找分割点（中位数）

我们要把点集在这一维上划分成两半，选中位数作为根节点。

如果用排序来找中位数，每层都要 O(n log n)，总复杂度 = O(n log^2 n)。

如果用「线性时间选择算法」（比如 quickselect），每层 O(n) 就够了，总复杂度可以降到 O(n log n)。

递归建树

左子树处理一半点，右子树处理另一半点。

总层数 ≈ log n（因为每次一分为二）。

🌟 最终时间复杂度

一般实现（每次排序）：O(n log^2 n)

优化实现（快速选择中位数）：O(n log n)

维度 k：通常被看作常数，对复杂度影响不大，但严格来说要乘个 k：

普通实现：O(k n log^2 n)

优化实现：O(k n log n)

🌟 一句话总结

构建 kd-tree 的时间复杂度 ≈ O(n log n)（采用快速选择中位数）。

如果偷懒直接排序，那就是 O(n log^2 n)。

🌟 建树过程
Step 1：根节点（按 x 坐标划分）

点数 = 7

按 x 排序：(1,5), (2,3), (4,7), (5,4), (7,2), (8,1), (9,6)

中位数是第 4 个点：(5,4)

根节点 = (5,4)

左子集 = [(1,5), (2,3), (4,7)]

右子集 = [(7,2), (8,1), (9,6)]

Step 2：左子树（按 y 坐标划分）

子集：(1,5), (2,3), (4,7)

按 y 排序：(2,3), (1,5), (4,7)

中位数 = (1,5)

左子树根 = (1,5)

左子集 = [(2,3)]

右子集 = [(4,7)]

Step 3：右子树（按 y 坐标划分）

子集：(7,2), (8,1), (9,6)

按 y 排序：(8,1), (7,2), (9,6)

中位数 = (7,2)

右子树根 = (7,2)

左子集 = [(8,1)]

右子集 = [(9,6)]

Step 4：继续递归（按 x 坐标划分）

(2,3)、(4,7)、(8,1)、(9,6) 都只剩 1 个点，不再划分。

🌟 最终 kd-tree 结构

         (5,4)        ← 根（x 分割）/       \(1,5)        (7,2)   ← 第二层（y 分割）/     \      /     \
(2,3) (4,7) (8,1) (9,6)

13. 三维空间最近邻搜索的常用数据结构

🌟 1. kd-tree （k-dimension tree）

原理：递归地用坐标轴方向切分空间（3D 就是 x/y/z 轮流切分），形成一棵二叉树。

优点：

构建复杂度 O(n log n)；

查询平均 O(log n)，比暴力 O(n) 快很多。

缺点：

维度升高时退化（curse of dimensionality），但在 3D 表现很好；

动态更新（频繁插入/删除）成本高。

应用：点云匹配（ICP）、最近邻查找、三维重建等。

常见实现：PCL（Point Cloud Library）的 KdTreeFLANN。

🌟 2. Octree （八叉树）

原理：递归划分立方体空间，每个节点划分成 8 个子立方体。

优点：

适合 3D 点云稀疏存储，空间分割直观；

支持近邻搜索和范围查询。

缺点：

不如 kd-tree 在“精确最近邻”上高效，适合近似搜索和范围查询。

应用：3D 地图（OctoMap）、体素滤波、点云压缩。

🌟 3. BVH （Bounding Volume Hierarchy，包围体层次）

原理：用包围盒（AABB、OBB、球体等）自顶向下递归包裹点/几何体，形成树结构。

优点：

在碰撞检测、光线追踪等应用中比 kd-tree 常用；

查询效率也接近 O(log n)。

缺点：

构建复杂度高；

主要针对几何体，而不是大规模点云。

🌟 4. R-tree / R*-tree

原理：用矩形（3D 就是长方体）作为节点的边界，适合做区间/范围查询。

优点：

适合数据库、GIS（地理信息系统），支持批量插入/删除；

动态更新比 kd-tree 好。

缺点：

精确最近邻性能比 kd-tree 略差。

🌟 5. 近似最近邻（ANN）结构

如果数据非常大，或者允许近似搜索，可以用哈希/投影类算法：

LSH（Locality Sensitive Hashing）：用哈希把相近的点映射到同一桶。

FLANN（Fast Library for Approximate Nearest Neighbors）：自动选择 kd-tree / k-means tree 混合结构。

FAISS（Facebook AI）：超大规模向量检索库。
👉 这些在 3D 点云搜索中用得不多，但在机器学习里很常见。

🌟 总结

在三维空间最近邻搜索里：

精确搜索 → kd-tree 最常用；

近似搜索、大规模点云 → Octree / FLANN；

碰撞检测 / 光线追踪 → BVH；

数据库 / GIS → R-tree。

14. 一层楼共有n级台阶，一次可以上至少一级但不超过m级台阶，求有多少种不同的上楼方案数。由于结果可能很大，你只需要输出结果对10007取模的值即可

思路：设走到第k阶台阶的走法数为f(k)，如果你现在在第 n 级台阶，可能是从第 n−1、n−2、…、n−m 过来的：
所以f(n) = f(n-1)+f(n-2)+…+f(n-m) ,它需要「最近的 m 个 f 值」的和
设计这个窗口就在于，把新得到的 f(n) 加进窗口，把最旧的 f(n−m) 移出窗口，计算窗口内m个f值的和，我们可以用循环数组或者双端队列实现
循环数组的方法：
1.新手方法，最朴素的递归

MOD = 10007def ways_recursive(n, m):"""最直观的递归解法"""if n == 0:return 1  # 到达台阶顶if n < 0:return 0  # 走过头，不算total = 0for k in range(1, m+1):  # 尝试走 1~m 步total += ways_recursive(n-k, m)return total % MOD

✅ 优点

代码最直观，完全符合题意定义。

容易理解，适合入门。

❌ 缺点

计算会大量重复，时间复杂度接近指数级。

n 稍微大一点（比如 30），就已经非常慢。

比如计算 f(5) 需要算 f(4) 和 f(3)，而计算 f(4) 又需要算 f(3) 和 f(2)。f(3) 被计算了多次。

进阶版：

MOD = 10007def ways_dp(n, m):"""用 DP 表格存储所有 f(0..n)"""f = [0] * (n + 1)f[0] = 1  # 初始状态for i in range(1, n+1):for k in range(1, m+1):if i - k >= 0:f[i] = (f[i] + f[i-k]) % MODreturn f[n]

递归是“自顶向下”：我们从目标 n 开始，问“要走到 n，需要先走到哪里？”，然后不断地问下去，直到问到已知的 f(0)=1。

DP是“自底向上”：我们从已知的 f(0)=1 开始，一步一步、从小到大地计算出所有台阶的方法数，直到算出我们想要的 f(n)。

k 的循环 (内层循环)：解决的是 “从哪来” 的问题。对于当前台阶 i，它可能的前序台阶是 i-1, i-2, …, i-m。这个循环就是在把这些来源的方案数加起来。

i 的循环 (外层循环)：解决的是 “计算顺序” 的问题。它保证了当我们计算 f[i] 时，所有需要的 f[i-1], f[i-2], … 都已经提前被计算好并存储在表格里了，我们可以直接查询使用，避免了递归的重复计算。

MOD = 10007def ways_dp(n, m):"""用 DP 表格存储所有 f(0..n)"""f = [0] * (n + 1)f[0] = 1  # 初始状态for i in range(1, n+1):for k in range(1, m+1):if i - k >= 0:f[i] = (f[i] + f[i-k]) % MODreturn f[n]

我们保存了整个数组 f[0…n]，所以内存是 O(n)。

但实际上，当你算到 f(i) 时，只会用到最近 m 个状态（即 f[i-1], f[i-2], …, f[i-m]）。

更远的 f(j) （比如 f[i-m-1]）再也不会被访问。

👉 所以保存整个 f[0…n] 是冗余的。

🚩 第一步优化 —— 只存最近 m 个值（循环数组）

思路：

我只要一块大小为 m+1 的循环数组 dp。

当 i 增加时，我把新算出来的 f[i] 存进去，同时覆盖掉「最老的那个已经没用了的值」。

这样空间复杂度从 O(n) → O(m)。

🚩 第二步优化 —— 再优化掉内层循环（滑动窗口）

问题：虽然只存了 m 个数，但每次算 f[i] 时还是要 for 循环加 m 项，时间复杂度还是 O(n·m)。

解决方法：

我们注意到 f[i] = f[i-1] + f[i-2] + … + f[i-m]，其实就是一个长度为 m 的滑动窗口和。

如果我们在算 f[i] 时维护一个变量 win 表示「最近 m 个 f 的和」，那么：

f[i] = win

下一步 f[i+1] = win + f[i] - f[i-m]

也就是说：
👉 我们不用每次都重新加 m 项，只要加新数、减旧数就行了。

这样时间复杂度从 O(n·m) → O(n)。

🚩设计细节 —— 如何“释放”旧的 f？

你提到的关键点就是：

计算 f[i] 之后，如何释放掉 f[i-m-1]？

在滑窗方案里：

用一个循环数组存最近 m 个值；

每次计算新的 f[i] 后：

把 f[i] 加入 win；

如果窗口长度超过 m，就从 win 中减去 f[i-m]；

同时，dp[(i-m) % (m+1)] 的位置就可以安全覆盖掉了（因为不会再用到）。

🚩 思维进化总结

递归版：定义问题。

DP 版：避免重复计算 → O(n·m)，但浪费内存。

循环数组：只保存最近 m 个 → O(m) 空间。

滑动窗口：维护窗口和 → O(n) 时间 + O(m) 空间。

3️⃣ 滑动窗口优化版

MOD = 10007def ways_window(n, m):"""滑动窗口优化 DP"""if n == 0:return 1dp = [0] * (m+1)  # 循环数组，只存最近 m 个dp[0] = 1         # f(0) = 1win = 1           # 窗口和，初始只有 f(0)fn = 0            # 保存当前结果for i in range(1, n+1):fn = win % MOD                # f(i) = 窗口和dp[i % (m+1)] = fn            # 存入循环数组win = (win + fn) % MOD        # 窗口 += 新的 f(i)if i - m >= 0:                # 超出 m 个时，减去最老的 f(i-m)old = dp[(i - m) % (m+1)]win = (win - old) % MODreturn fn % MOD

节省空间和时间。

目的：处理超大规模 n。

手段：只保存最近 m 个值，用窗口和快速更新。

你可以把 dp 想象成一个旋转餐盘：

一共 m+1 个盘子位置。

每次上新菜（f(i)），把它放到 (i % (m+1)) 的盘子上。

同时把盘子里最旧的菜（f(i-m)）拿走。

因为餐盘有 m+1 个位置，转一圈后新菜才会覆盖到最老的那个盘子，所以不会误删。
“f(0)充当了一个占位” 完全正确，它既是数学上的基准条件，又是程序实现上的缓冲位，让整个滑动窗口逻辑既正确又优雅。

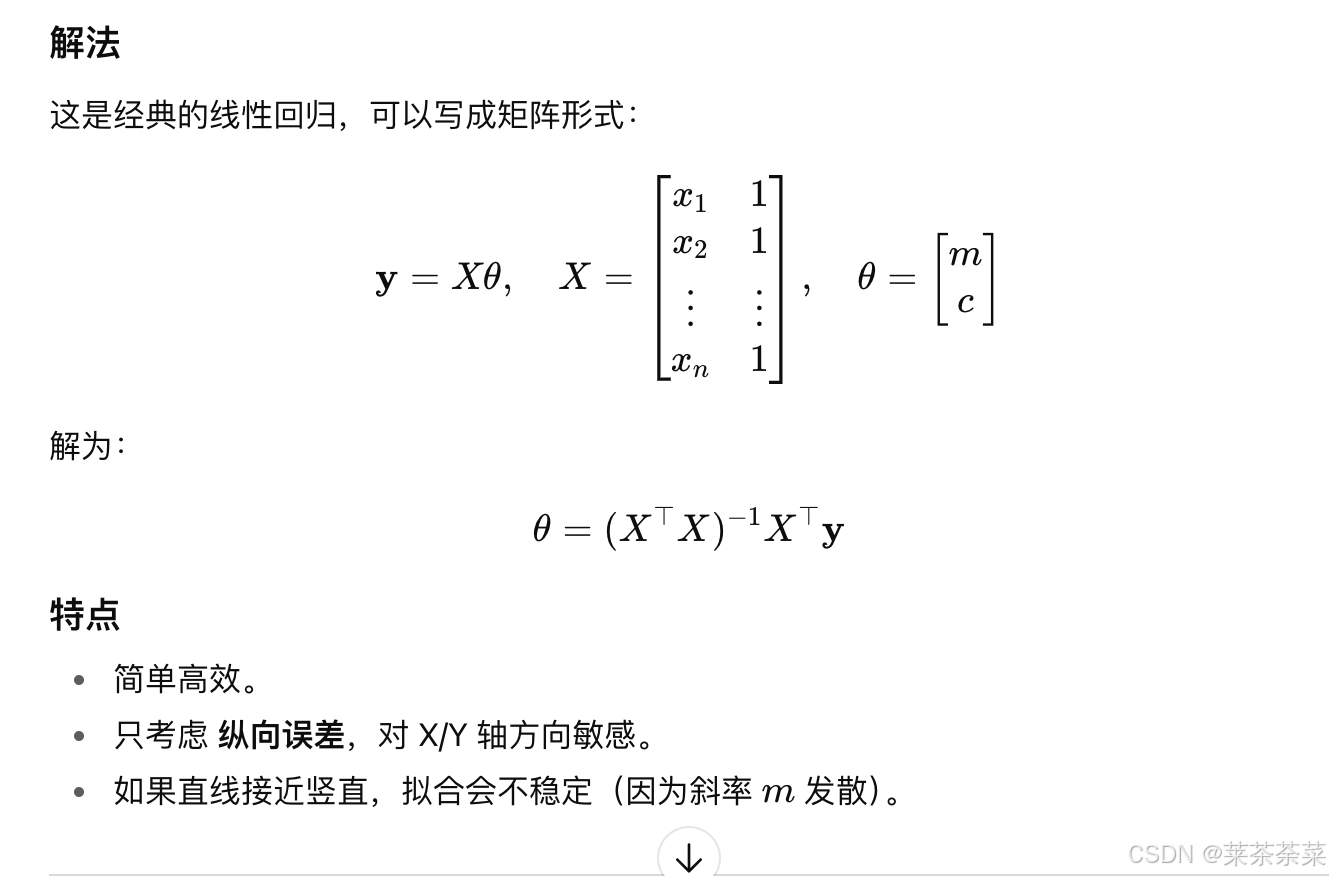
15. 拟合二维平面中的带噪声直线，其中有不超过20%的样本点远离了直线，另外80%的样本点可能有高斯噪声的偏移，要求输出为ax+by+c=0的形式，其中a>0且 $a^2 + b^2=1$

可以把它当成“有离群点的总最小二乘直线拟合”问题来做：先用 RANSAC 抗 20% 离群点找出内点集合，再用总最小二乘（TLS/PCA）在内点上精修，最后把系数归一化并令 a>0。

下面给出一段可直接用的 Python 实现（仅依赖 numpy）。输出满足你要的形式 ax+by+c=0、a>0、 $a^2 + b^2 = 1$

import numpy as npdef fit_line_robust(points, max_trials=200, seed=None):"""Robustly fit a 2D line ax + by + c = 0 with a>0 and a^2+b^2=1.Assumes up to ~20% outliers; inliers may have Gaussian noise.points: (N,2) array of [x,y].Returns: a, b, c, inlier_mask (boolean array of length N)"""pts = np.asarray(points, dtype=float)N = pts.shape[0]if N < 2:raise ValueError("Need at least 2 points.")rng = np.random.default_rng(seed)best_inliers = Nonebest_count = -1best_model = Nonefor _ in range(max_trials):# 1) 随机两点确定一条候选直线i, j = rng.choice(N, size=2, replace=False)p1, p2 = pts[i], pts[j]v = p2 - p1if np.allclose(v, 0):continue# 法向量 n = (dy, -dx)，并单位化 -> (a,b)n = np.array([v[1], -v[0]], dtype=float)norm_n = np.linalg.norm(n)if norm_n == 0:continuea, b = n / norm_n# c 使直线过 p1c = -(a * p1[0] + b * p1[1])# 2) 计算所有点到直线的正交距离 |ax+by+c|d = np.abs(a * pts[:, 0] + b * pts[:, 1] + c)# 3) 自适应阈值：用 MAD 估计噪声尺度md = np.median(d)sigma = 1.4826 * md + 1e-12          # 防止零thr = 2.5 * sigma                     # ~2.5σ 作为内点阈值inliers = d < thrcnt = int(inliers.sum())if cnt > best_count:best_count = cntbest_inliers = inliersbest_model = (a, b, c)if best_inliers is None or best_count < 2:raise RuntimeError("Failed to find a valid consensus set.")# 4) 在内点上做总最小二乘（PCA）精修P = pts[best_inliers]mu = P.mean(axis=0)Q = P - mu# PCA: 主方向是第一奇异向量_, _, Vt = np.linalg.svd(Q, full_matrices=False)direction = Vt[0]                       # 直线方向向量normal = np.array([direction[1], -direction[0]], dtype=float)normal /= np.linalg.norm(normal)        # 单位法向量 -> (a,b)a, b = normalc = -(a * mu[0] + b * mu[1])            # 使直线过内点均值# 5) 规范化：a>0，且已经保证 a^2+b^2=1if a < 0:a, b, c = -a, -b, -creturn a, b, c, best_inliers# ========= 使用示例 =========
if __name__ == "__main__":# 生成一条 y = 0.5x + 1 的带噪数据，并加 20% 离群点rng = np.random.default_rng(0)x = np.linspace(-10, 10, 200)y = 0.5 * x + 1 + rng.normal(0, 0.3, size=x.size)  # 高斯噪声P = np.c_[x, y]# 添加离群点M = 40outliers = np.c_[rng.uniform(-10, 10, M), rng.uniform(-10, 10, M)]data = np.vstack([P, outliers])a, b, c, mask = fit_line_robust(data, max_trials=200, seed=42)print(f"a={a:.6f}, b={b:.6f}, c={c:.6f},  a^2+b^2={a*a+b*b:.6f}, a>0={a>0}")print(f"inliers: {mask.sum()}/{data.shape[0]}")

RANSAC
📌 背景:
在拟合模型时（比如直线、平面、单应矩阵等），数据往往包含：

内点 (inliers)：基本遵循某个数学模型，只是有随机噪声。
外点 (outliers)：完全不符合模型，可能是测量错误、遮挡、异常值。

普通的最小二乘法对外点很敏感：即便只有少量外点，也可能把拟合结果严重拉偏。
RANSAC就是为了解决“在含有外点的数据中鲁棒拟合模型”的问题。

📌 典型流程（以直线拟合为例）

随机采样从所有点中随机选出最小样本子集（比如拟合直线只需 2 点）。用这几个点拟合一个候选模型。

验证一致性将所有数据点代入候选模型，计算它们与模型的“残差”或“误差”。（比如直线时用点到直线的垂直距离）,设置一个阈值 T，若误差 < T，则认为该点是内点。

统计一致集大小统计候选模型对应的内点数（即一致集大小）。内点越多，说明该模型越可信。

重复迭代重复步骤 1–3 若干次（迭代次数 N），不断更新“目前为止最佳模型”。选择最佳模型找到拥有最大内点数的一致集，认为这是最终的内点集合。

精修模型用一致集（大多数是内点）做更精确的拟合（比如最小二乘/TLS）。得到最终鲁棒的模型。