吴恩达机器学习作业十 PCA主成分分析
数据集在作业一
PCA主成分分析
主成分分析(Principal Component Analysis,简称 PCA) 是一种常用的数据降维技术,其核心思想是通过线性变换将高维数据映射到低维空间,同时尽可能保留原始数据的关键信息(即方差最大的方向)。
具体来说,PCA 会在高维数据中寻找一组相互正交的坐标轴(主成分),这些坐标轴是数据方差最大的方向。其中,第一个主成分对应数据方差最大的方向,第二个主成分对应与第一个主成分正交且方差次大的方向,以此类推。通过保留前k个主成分(k远小于原始数据维度),可以在损失较少信息的前提下,将数据从高维降至k维,从而简化数据结构、减少计算量,并有助于可视化或后续建模。(这里的正交和方差都是为了确保信息保留最大化)
数学原理
为了能尽可能的保留数据,PCA要求投影方向正交,且方差最大,保证数据尽量不重复。
注意,上面的话语是我们的目的,下面的一切都是围绕方差最大且正交来进行。



这里涉及了较多的线性代数知识,如果不太能弄懂或者忘了,可以乘机补一下。
算法流程
1.数据预处理(均值归一化)
2.计算协方差矩阵以及它的特征向量(通过SVD计算)
3.进行投影
代码
读取数据及可视化
import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio# 读取数据
data=sio.loadmat("ex7data1.mat")
X=data['X']
# print(X.shape)(50, 2)# plt.scatter(X[:,0],X[:,1],marker='o',c='y',edgecolors='g')
# plt.show()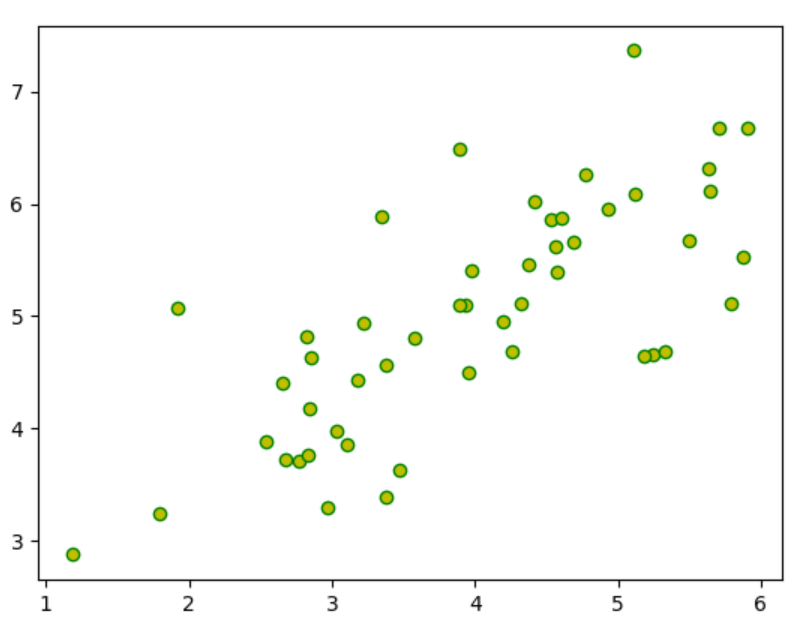
数据标准化及可视化
def demean(X):mu=np.mean(X,axis=0)sigma=np.std(X,axis=0,ddof=1)X=(X-mu)/sigmareturn X,mu,sigmaX_demean,mu,sigma=demean(X)
# 可视化
# plt.scatter(X_demean[:,0],X_demean[:,1],marker='o',c='y',edgecolors='g')
# plt.show()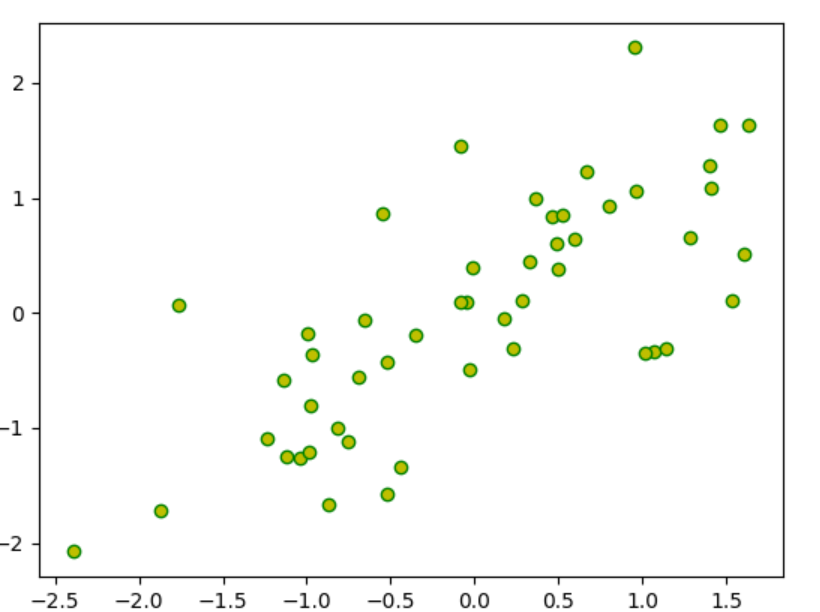
计算协方差矩阵和特征向量
def PCA(X):m=len(X)C=(X.T@X)/mU,S,V=np.linalg.svd(C)return U,SU,S=PCA(X_demean)这一切都是按照上面的数学原理进行计算的,
S中的每个元素表示对应主成分方向上的 “方差大小”(即该主成分所包含的原始数据信息量)。U的每一列是协方差矩阵C的一个特征向量,代表数据中一个 “主成分方向”(即数据方差最大的方向)。
可视化特征向量
plt.scatter(X[:,0],X[:,1],marker='o',c='y',edgecolors='g')
plt.plot([mu[0],mu[0]+1.5*S[0]*U[0,0]],[mu[1],mu[1]+1.5*S[0]*U[1,0]],c='k')
plt.plot([mu[0],mu[0]+1.5*S[1]*U[0,1]],[mu[1],mu[1]+1.5*S[1]*U[1,1]],c='k')
plt.title('Computed eigenvectors of the dataset')
plt.show()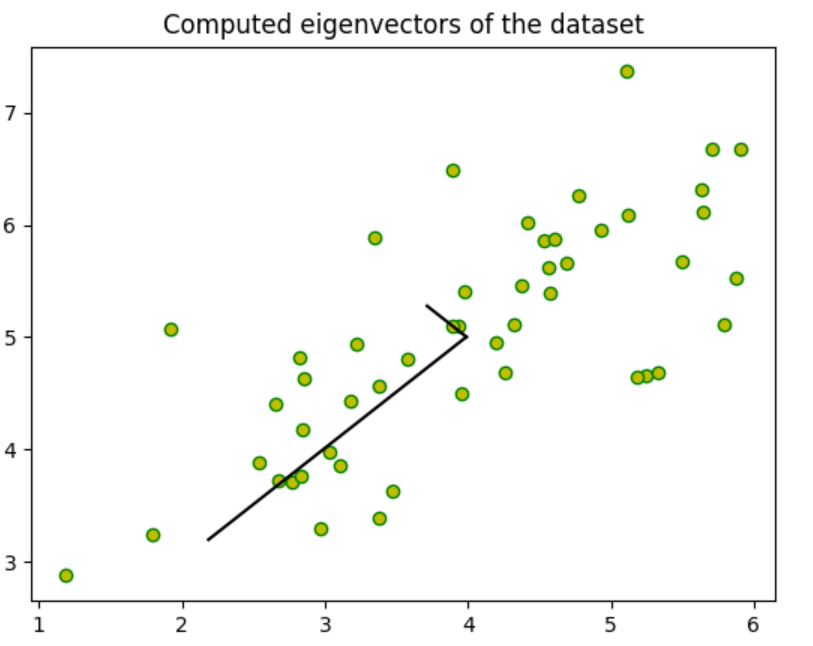
代码通过两条线段绘制两个主成分的方向,线段的起点是数据中心
mu,终点由 “方向向量 + 特征值缩放” 决定:U[0,0]和U[1,0]是第一主成分方向向量U[:,0]的 x、y 分量;S[0]是第一主成分的特征值(表示该方向的方差大小);1.5 * S[0]是对方向向量的缩放系数,控制线段长度(特征值越大,线段越长,直观体现方差大小)。U[0,0]和U[1,0]是第一主成分方向向量U[:,0]的 x、y 分量;S[0]是第一主成分的特征值(表示该方向的方差大小);1.5 * S[0]是对方向向量的缩放系数,控制线段长度(特征值越大,线段越长,直观体现方差大小)。
将数据映射到新空间
def project_data(X,U,k):Z=X@U[:,:k]return Z
Z=project_data(X_demean,U,1)
重建数据
def recover_data(Z,U,k):X_rec=Z@U[:,:k].Treturn X_recX_rec=recover_data(Z,U,1)可视化
# 可视化投影
# plt.scatter(X_demean[:,0],X_demean[:,1],marker='o',c='y',edgecolors='g')
# plt.scatter(X_rec[:,0],X_rec[:,1],marker='o',c='r',edgecolors='b')
# for i in range(len(X)):
# plt.plot([X_demean[i,0],X_rec[i,0]],[X_demean[i,1],X_rec[i,1]],c='k')
# plt.show()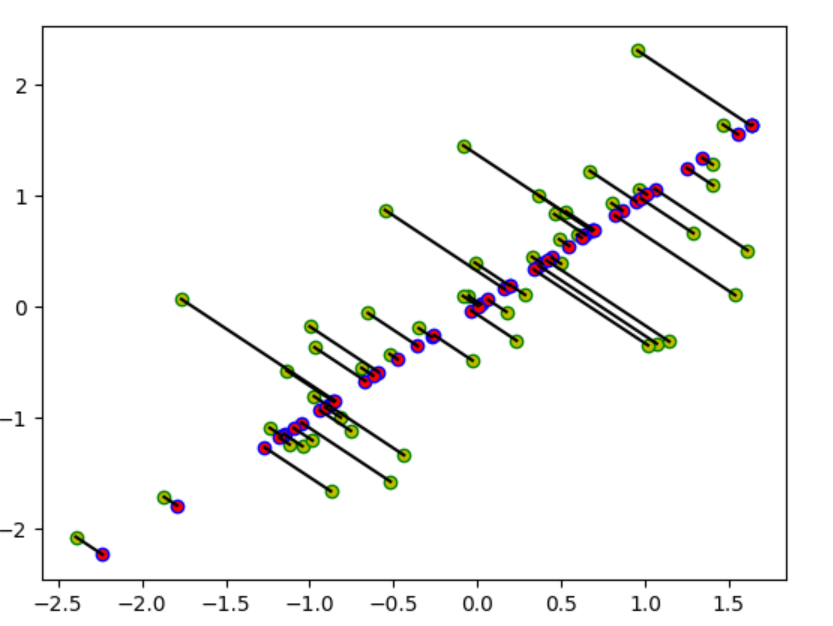
里面的红色是投影形成的。
查看差异保留
def display_data(S,k):rv=np.sum(S[:k])/np.sum(S)return rvrv=display_data(S,1)
print(rv)#0.8677651881696647总结
导入数据——数据标准化——通过取协方差矩阵的特征向量作为投影方向——数据映射——数据恢复——比较差异
