算法 --- 前缀和

前缀和

前缀和算法主要用于高效处理“连续子数组区间求和”问题，其核心是通过预处理得到一个前缀和数组，从而将原本每次需要 O(n^x) 时间的区间求和操作优化到 O(n^x-1) 时间。

---

详细说明与应用场景

1. 什么是前缀和？

前缀和是一个简单的预处理技巧。给定一个数组 nums，我们创建一个长度為 n+1 的前缀和数组 prefixSum，其中：

• prefixSum[0] = 0

• prefixSum[i] = nums[0] + nums[1] + ... + nums[i-1]

这样，数组中任意一段区间 [left, right]（闭区间）的和，就可以通过一次减法快速计算：
sum(left, right) = prefixSum[right+1] - prefixSum[left]

2. 什么样的题目适用前缀和？

前缀和并非万能，它专门攻克以下几类典型问题：

a) 频繁计算静态数组的区间和
这是最直接的应用。如果题目要求你多次查询同一个数组的不同子数组的和，前缀和是标准解法。

• 例题：LeetCode 303. 区域和检索 - 数组不可变

b) 求满足特定条件的子数组个数（核心应用）
这是前缀和，尤其是结合哈希表技巧的最高频考点。常见条件包括：

• 子数组和为 K：求有多少个连续子数组的和等于目标值 K。

  • 思路：计算前缀和数组 prefix，问题转化为寻找有多少对 (i, j)，使得 prefix[j] - prefix[i] = k。这可以通过一个哈希表在遍历时记录之前出现过的前缀和及其次数来高效解决。

  • 例题：LeetCode 560. 和为 K 的子数组

• 子数组和可被整除：求有多少个连续子数组的和能被 k 整除。

  • 思路：计算前缀和数组，并对 k 取模。根据同余定理，如果 prefix[i] % k == prefix[j] % k，那么区间 [i, j] 的和必然能被 k 整除。问题转化为寻找相同余数出现的次数。

  • 例题：LeetCode 974. 和可被 K 整除的子数组

• 子数组平均值为某数：例如，求长度为 k 的子数组平均值大于 threshold 的个数。

  • 思路：先用前缀和快速计算每个长度为 k 的子数组和，然后与 k * threshold 比较即可。

  • 例题：LeetCode 1343. 大小为 K 且平均值大于等于阈值的子数组数目

c) 二维（甚至多维）区域和检索
前缀和可以自然地扩展到二维，用于快速计算矩阵中任意矩形区域的和。

• 定义：prefixSum[i][j] 表示从 (0,0) 到 (i-1, j-1) 的矩形区域和。

• 计算公式：sumRegion(row1, col1, row2, col2) = prefixSum[row2+1][col2+1] - prefixSum[row1][col2+1] - prefixSum[row2+1][col1] + prefixSum[row1][col1]

• 例题：LeetCode 304. 二维区域和检索 - 矩阵不可变

3. 什么情况下不适用前缀和？

• 数组是动态变化的：如果原数组在多次查询之间会被频繁修改，那么每次修改都需要更新整个前缀和数组，时间复杂度为 O(n)，效率低下。这种情况下应使用 线段树 或 树状数组。

• 问题与“区间和”无关：如果问题核心是求区间最大值、最小值或其他属性，前缀和就无能为力了。

总结

当你看到题目包含以下关键词时，应优先考虑前缀和：

• 连续子数组

• 和 / 求和

• 区间和

• 多次查询

其解题模式非常固定：预处理得到前缀和数组 -> 将原问题转化为基于前缀和的问题 -> 使用遍历或哈希表寻找答案。掌握这个模式，就能解决一大类高频算法题。

题目练习

【模板】前缀和_牛客题霸_牛客网

解法（前缀和）：

算法思路：

a. 先预处理出来一个「前缀和」数组：

• 用 dp[i] 表示：[1, i] 区间内所有元素的和，那么 dp[i - 1] 里面存的就是 [1, i - 1] 区间内所有元素的和，那么：可得递推公式：dp[i] = dp[i - 1] + arr[i];

b. 使用前缀和数组，「快速」求出「某一个区间内」所有元素的和：

• 当询问的区间是 [l, r] 时：区间内所有元素的和为：dp[r] - dp[l - 1]。

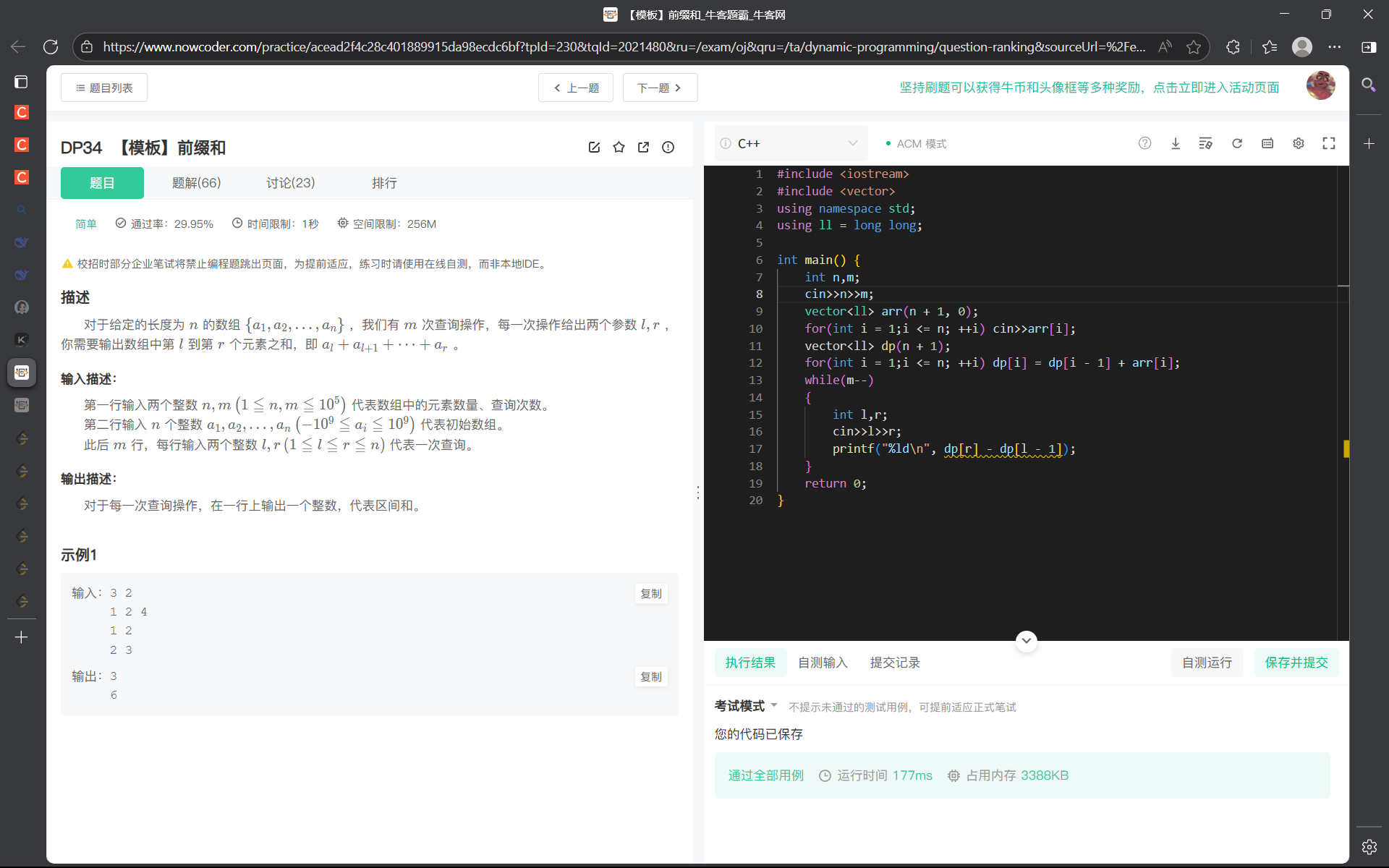
【模板】二维前缀和_牛客题霸_牛客网

解法（前缀和）：

算法思路：

类似于一维数组的形式，如果我们能处理出来从 [0, 0] 位置到 [i, j] 位置这片区域内所有元素的累加和，就可以在 O(1) 的时间内，搞定矩阵内任意区域内所有元素的累加和。因此我们接下来仅需完成两步即可：

第一步：搞出来前缀和矩阵

这里就要用到一维数组里面的拓展知识，我们要在矩阵的最上面和最左边添加上一行和一列 0，这样我们就可以省去非常多的边界条件的处理（同学们可以自行尝试直接搞出来前缀和矩阵，边界条件的处理会让你崩溃的）。处理后的矩阵就像这样：

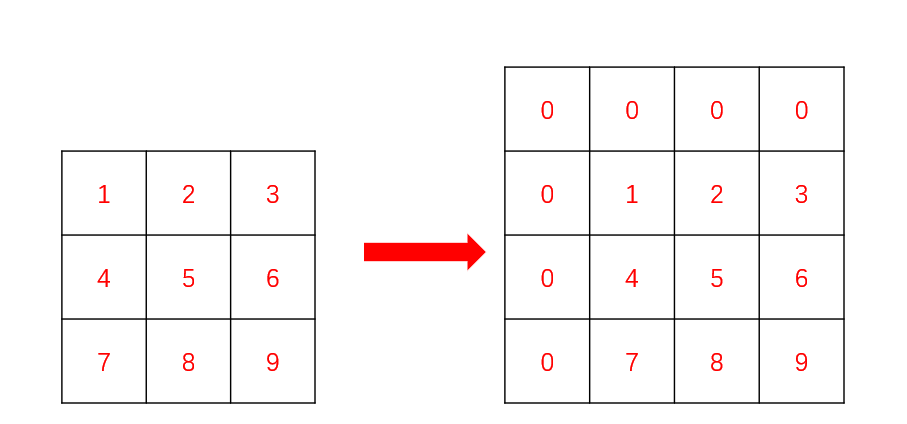
这样，我们填写前缀和矩阵数组的时候，下标直接从 1 开始，能大胆使用 i−1，j−1 位置的值。

注意 dp 表与原数组 matrix 内的元素的映射关系：

• 从 dp 表到 matrix 矩阵，横纵坐标减一；

• 从 matrix 矩阵到 dp 表，横纵坐标加一。

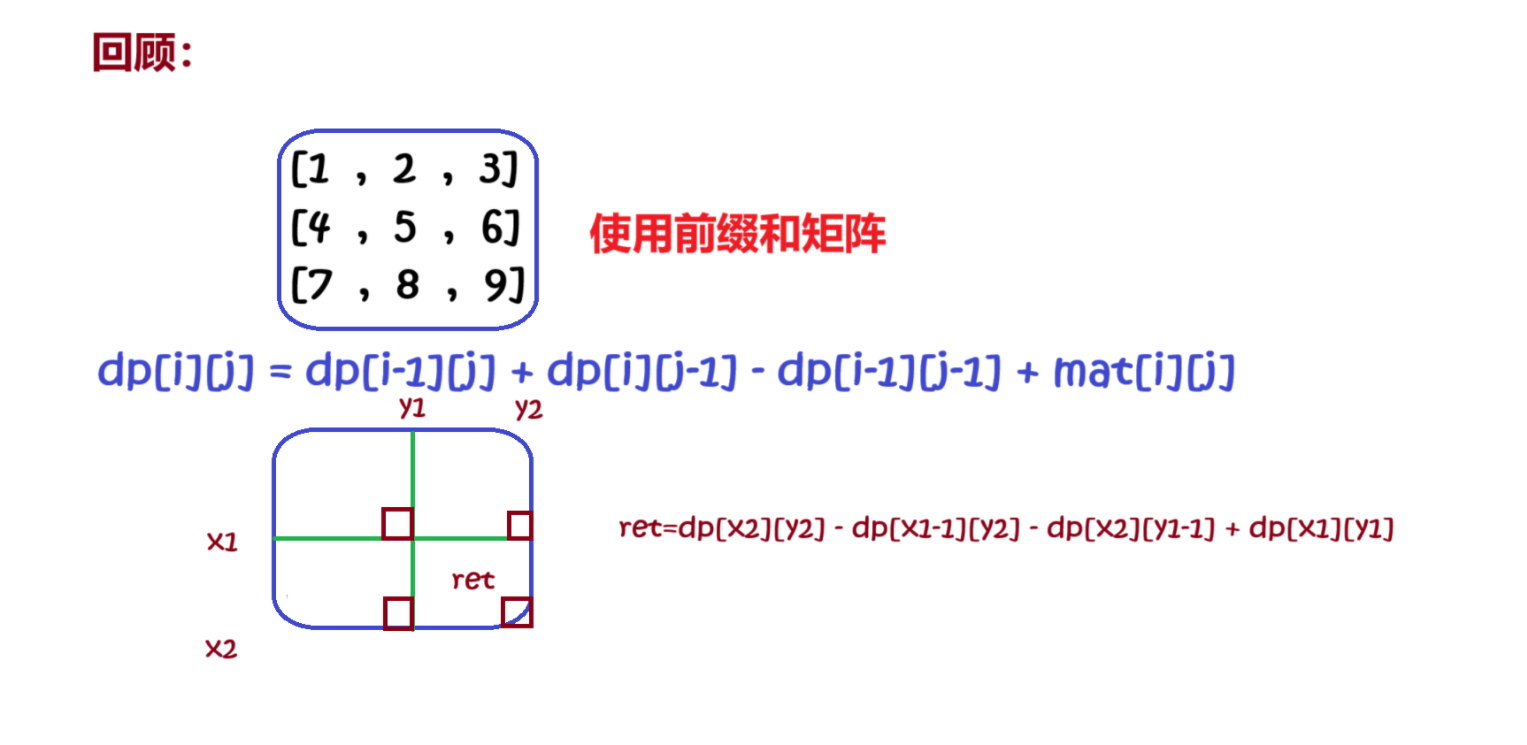
前缀和矩阵中 sum[i][j] 的含义以及如何递推二维前缀和方程：

a. sum[i][j] 的含义：

sum[i][j] 表示，从 [0, 0] 位置到 [i, j] 位置这段区域内，所有元素的累加和。对应下图的红色区域：

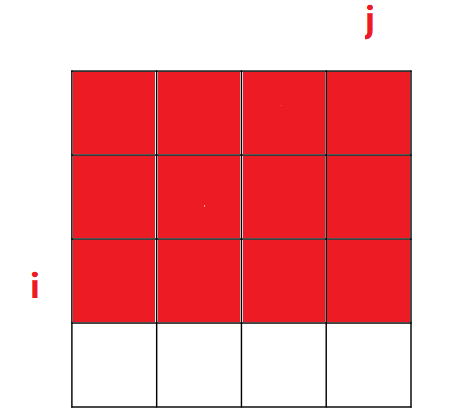
b. 递推方程：

其实这个递推方程非常像我们小学做过求图形面积的题，我们可以将 [0, 0] 位置到 [i, j] 位置这段区域分解成下面的部分：

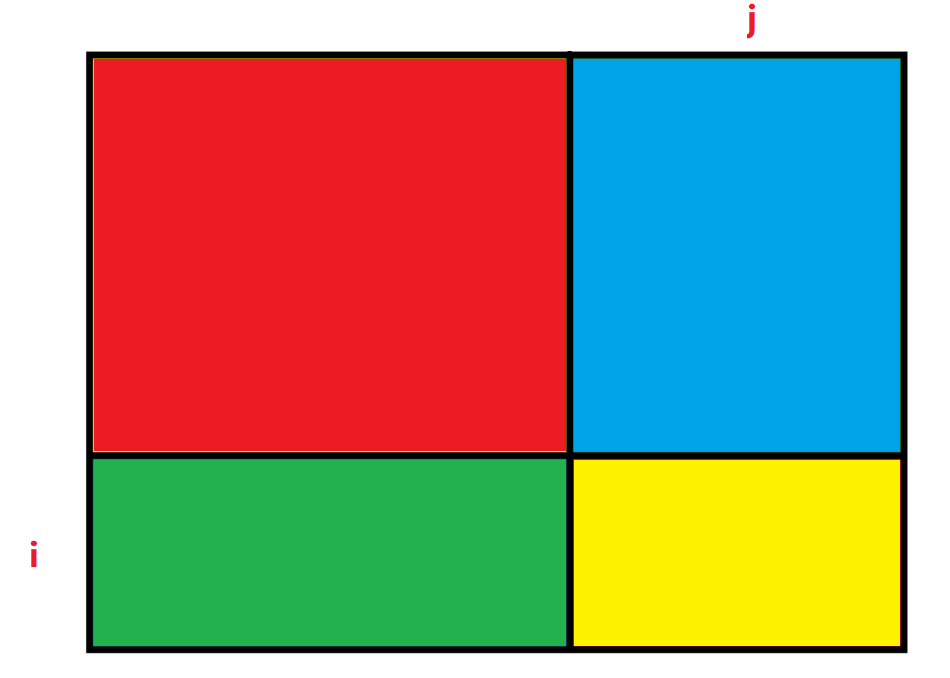
sum[i][j]= 红 + 蓝 + 绿 + 黄，分析一下这四块区域：

i. 黄色部分最简单，它就是数组中的 matrix[i−1][j−1]（注意坐标的映射关系）

ii. 单独的蓝不好求，因为它不是我们定义的状态表示中的区域，同理，单独的绿也是；

iii. 但是如果是红 + 蓝，正好是我们 dp 数组中 sum[i−1][j] 的值，美滋滋；

iv. 同理，如果是红 + 绿，正好是我们 dp 数组中 sum[i][j−1] 的值；

v. 如果把上面求的三个值加起来，那就是黄 + 红 + 蓝 + 红 + 绿，发现多算了一部分红的面积，因此再单独减去红的面积即可；

vi. 红的面积正好也是符合 dp 数组的定义的，即 sum[i−1][j−1]

综上所述，我们的递推方程就是：

sum[i][j]=sum[i−1][j]+sum[i][j−1]−sum[i−1][j−1]+matrix[i−1][j−1]

第二步：使用前缀和矩阵

题目的接口中提供的参数是原始矩阵的下标，为了避免下标映射错误，这里直接先把下标映射成 dp 表里面对应的下标：row1++，col1++，row2++，col2++。

接下来分析如何使用这个前缀和矩阵，如下图（注意这里的 row 和 col 都处理过了，对应的正是 sum 矩阵中的下标）：

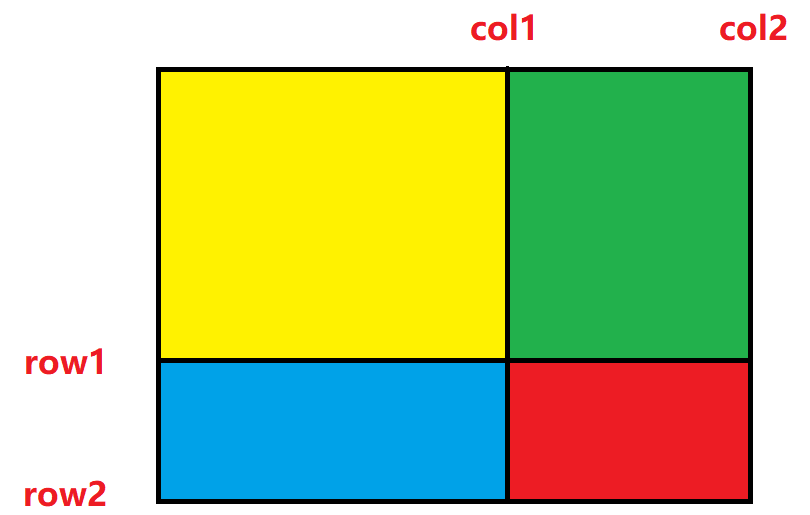
对于左上角（row1，col1）和右下角（row2，col2）围成的区域，正好是红色的部分。因此我们要求的就是红色部分的面积，继续分析几个区域：

i. 黄色，能直接求出来，就是 sum[row2−1][col2−1]（为什么减一？因为要删除掉 row 这一行和 col 这一列）

ii. 绿色，直接求不好求，但是和黄色拼起来，正好是 sum 表示 sum[row1−1][col2] 的数据。

iii. 同理，蓝色不好求，但是蓝 + 黄 = sum[row2][col1−1]；

iv. 再看看整个面积，好求啊，好求啊，正好是 sum[row2][col2]；

v. 那么，红色就 = 整个面积 - 黄 - 绿 - 蓝，但是绿蓝不好求，我们可以这样减：整个面积 - （绿 + 黄） - （蓝 + 黄），这样相当于多减去了一个黄，用上即可

综上所述：红色面积 = 整个面积 - （绿 + 黄） - （蓝 + 黄），从而可得红色区域内的元素总和为：

sum[row2][col2]−sum[row2][col1−1]−sum[row1−1][col2]+sum[row1−1][col1−1]

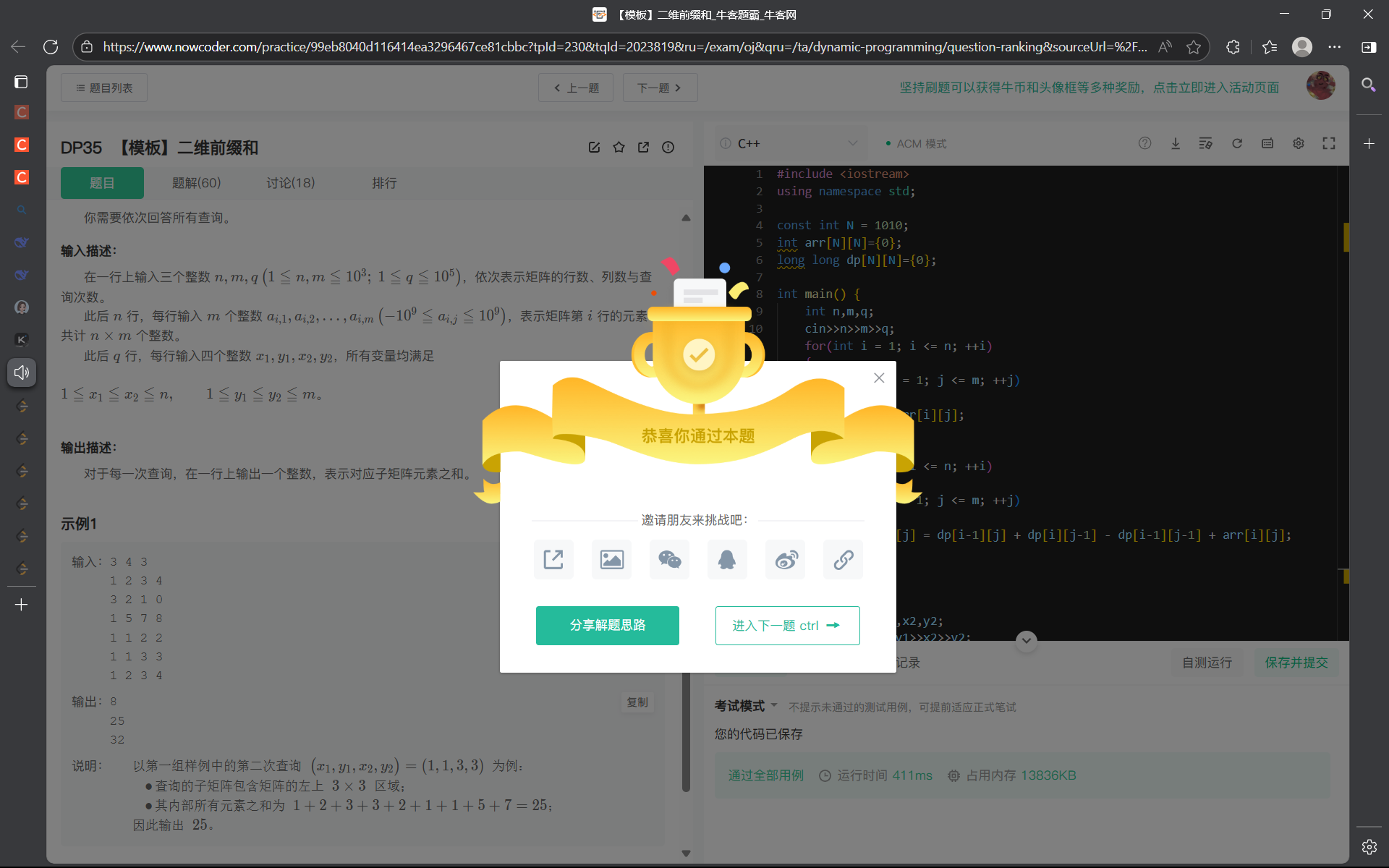
724. 寻找数组的中心下标 - 力扣（LeetCode）

解法（前缀和）：

算法思路：

从中心下标的定义可知，除中心下标的元素外，该元素左边的「前缀和」等于该元素右边的「后缀和」。

• 因此，我们可以先预处理出来两个数组，一个表示前缀和，另一个表示后缀和。

• 然后，我们可以用一个 for 循环枚举可能的中心下标，判断每一个位置的「前缀和」以及「后缀和」，如果二者相等，就返回当前下标。

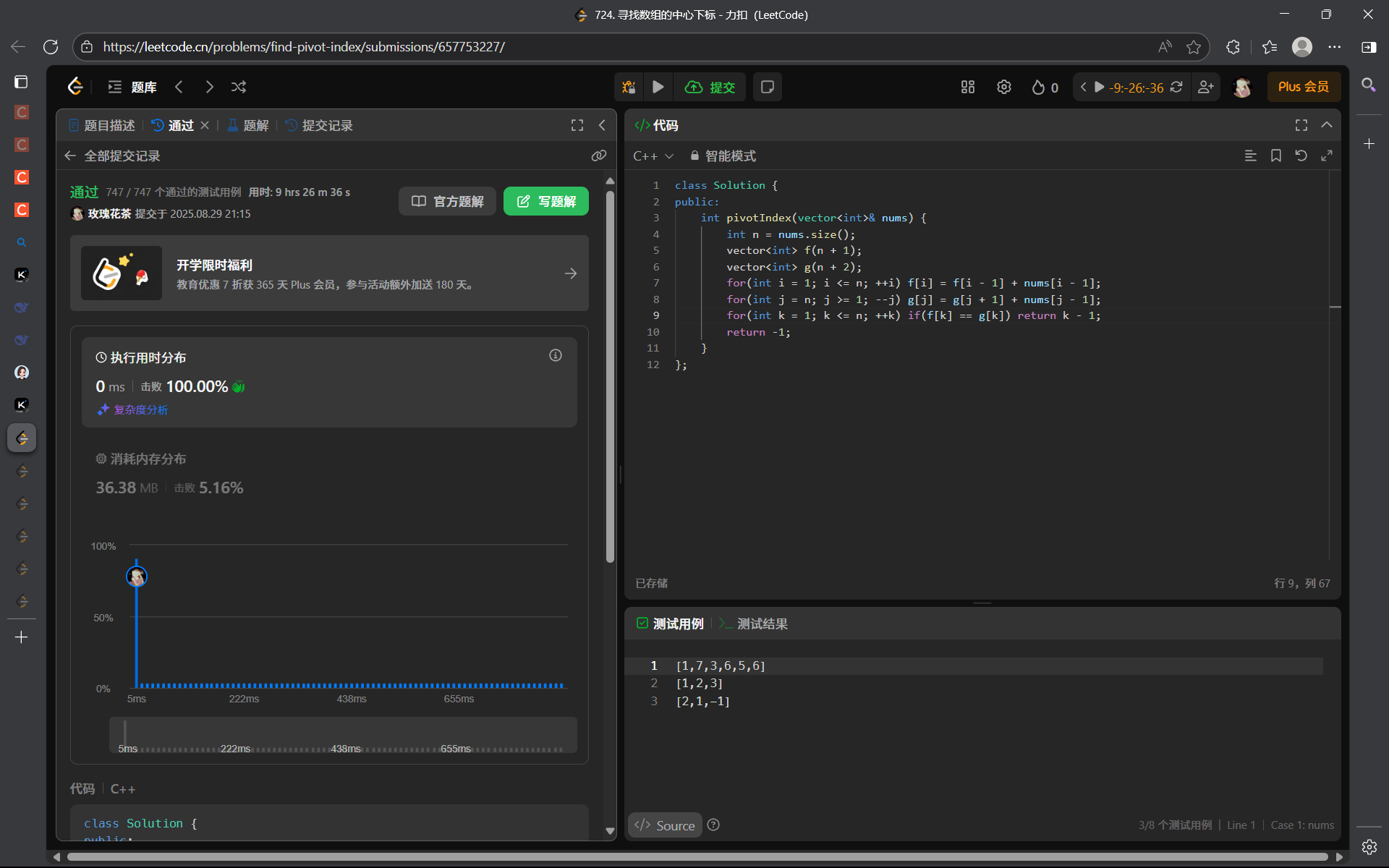
238. 除自身以外数组的乘积 - 力扣（LeetCode）

解法（前缀和数组）：

算法思路：

注意题目的要求，不能使用除法，并且要在 O(N) 的时间复杂度内完成该题。那么我们就不能使用暴力的解法，以及求出整个数组的乘积，然后除以单个元素的方法。

继续分析，根据题意，对于每一个位置的最终结果 ret[i]，它是由两部分组成的：

i. nums[0]×nums[1]×nums[2]×…×nums[i−1]

ii. nums[i+1]×nums[i+2]×…×nums[n−1]

于是，我们可以利用前缀和的思想，使用两个数组 post 和 suf，分别处理出来两个信息：

• post 表示：i 位置之前的所有元素，即 [0, i - 1] 区间内所有元素的前缀乘积；

• suf 表示：i 位置之后的所有元素，即 [i + 1, n - 1] 区间内所有元素的后缀乘积

然后再处理最终结果。

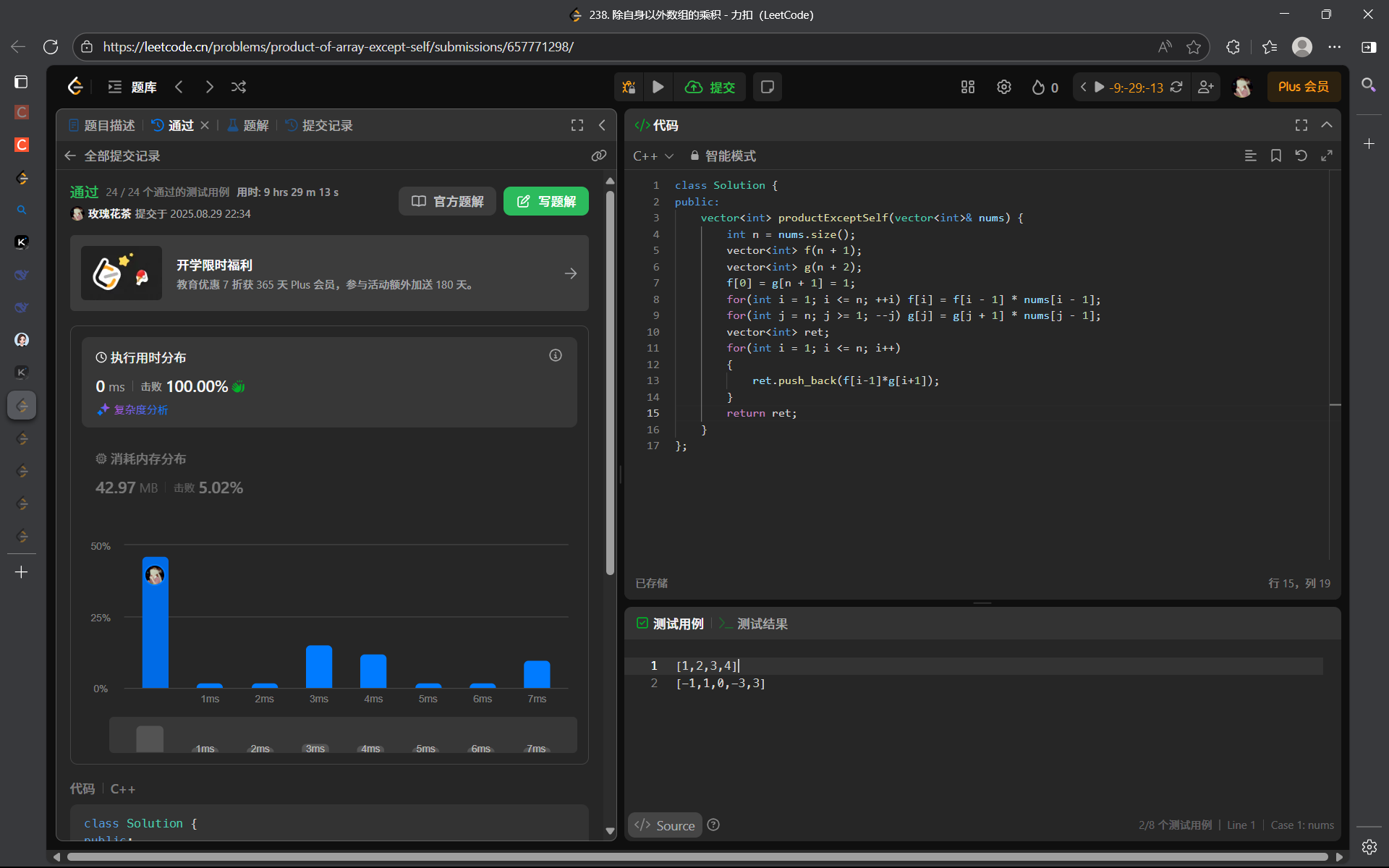
560. 和为 K 的子数组 - 力扣（LeetCode）

解法一（将前缀和存在哈希表中）：

算法思路：

设 i 为数组中的任意位置，用 sum[i] 表示 [0, i] 区间内所有元素的和。

想知道有多少个「以 i 为结尾的和 k 的子数组」，就要找到有多少个起始位置为 x1​,x2​,x3​,… 使得 [x, i] 区间内的所有元素的和为 k。那么 [0, x] 区间内的和是不是就是 sum[i]−k 了。于是问题就变成：

• 找到在 [0, i - 1] 区间内，有多少前缀和等于 sum[i]−k 的即可。

我们不用真的初始化一个前缀和数组，因为我们只关心在 i 位置之前，有多少个前缀和等于 sum[i]−k。因此，我们仅需用一个哈希表，一边求当前位置的前缀和，一边存下之前每一种前缀和出现的次数。

我们此题无法使用双指针是因为有负值，没有满足单调性等规律，无法将结果全部列出来！

974. 和可被 K 整除的子数组 - 力扣（LeetCode）

 解法（前缀和在哈希表中）：

算法思路：

本题需要的前置知识：

• 同余定理
  如果 (a−b)%n==0，那么我们可以得到一个结论：a%n==b%n。用文字叙述就是，如果两个数相减的差能被 n 整除，那么这两个数对 n 取模的结果相同。

例如：(26−2)%12==0，那么 26%12==2%12==2。

• C++ 中负数取模的结果，以及如何修正「负数取模」的结果
  a. C++ 中关于负数的取模运算，结果是「把负数当成正数，取模之后的结果加上一个负号」。
  例如：−1%3=−(1%3)=−1
  b. 因为有负数，为了防止发生「出现负数」的结果，以 (a%n+n)%n 的形式输出保证为正。
  例如：(−1%3)=(−1%3+3)%3=2

算法思路：

思路与 560. 和为 K 的子数组 这道题的思路相似。

设 i 为数组中的任意位置，用 sum[i] 表示 [0, i] 区间内所有元素的和。

• 想知道有多少个「以 i 为结尾的和 k 的子数组」，就要找到有多少个起始位置为 x1​,x2​,x3​,… 使得 [x, i] 区间内的所有元素的和为 k。那么 [0, x] 区间内的和是不是就是 sum[i]−k 了。于是问题就变成：

  • 找到在 [0, i - 1] 区间内，有多少前缀和等于 sum[i]−k 的即可。

我们不用真的初始化一个前缀和数组，因为我们只关心在 i 位置之前，有多少个前缀和等于 sum[i]−k。因此，我们仅需用一个哈希表，一边求当前位置的前缀和，一边存下之前每一种前缀和出现的次数。

525. 连续数组 - 力扣（LeetCode）

解法（前缀和在哈希表中）：

算法思路：

稍微转化一下题目，就会变成我们熟悉的题：

• 本题让我们找出一段连续的区间，0 和 1 出现的次数相同。

• 如果将 0 记为 -1，1 记为 1，问题就变成了找出一段区间，这段区间的和等于 0。

• 于是，就和 560. 和为 K 的子数组 这道题的思路一样。

设 i 为数组中的任意位置，用 sum[i] 表示 [0, i] 区间内所有元素的和。

• 想知道最大的「以 i 为结尾的和为 0 的子数组」，就要找到从左往右第一个 x1​ 使得 [x_1, i] 区间内的所有元素的和为 0。那么 [0, x_1 - 1] 区间内的和是不是就是 sum[i] 了。于是问题变成：

  • 找到在 [0, i - 1] 区间内，第一次出现 sum[i] 的位置即可。

我们不用真的初始化一个前缀和数组，因为我们只关心在 i 位置之前，第一个前缀和等于 sum[i] 的位置。因此，我们仅需用一个哈希表，一边求当前位置的前缀和，一边存下之前每一种前缀和出现的次数。

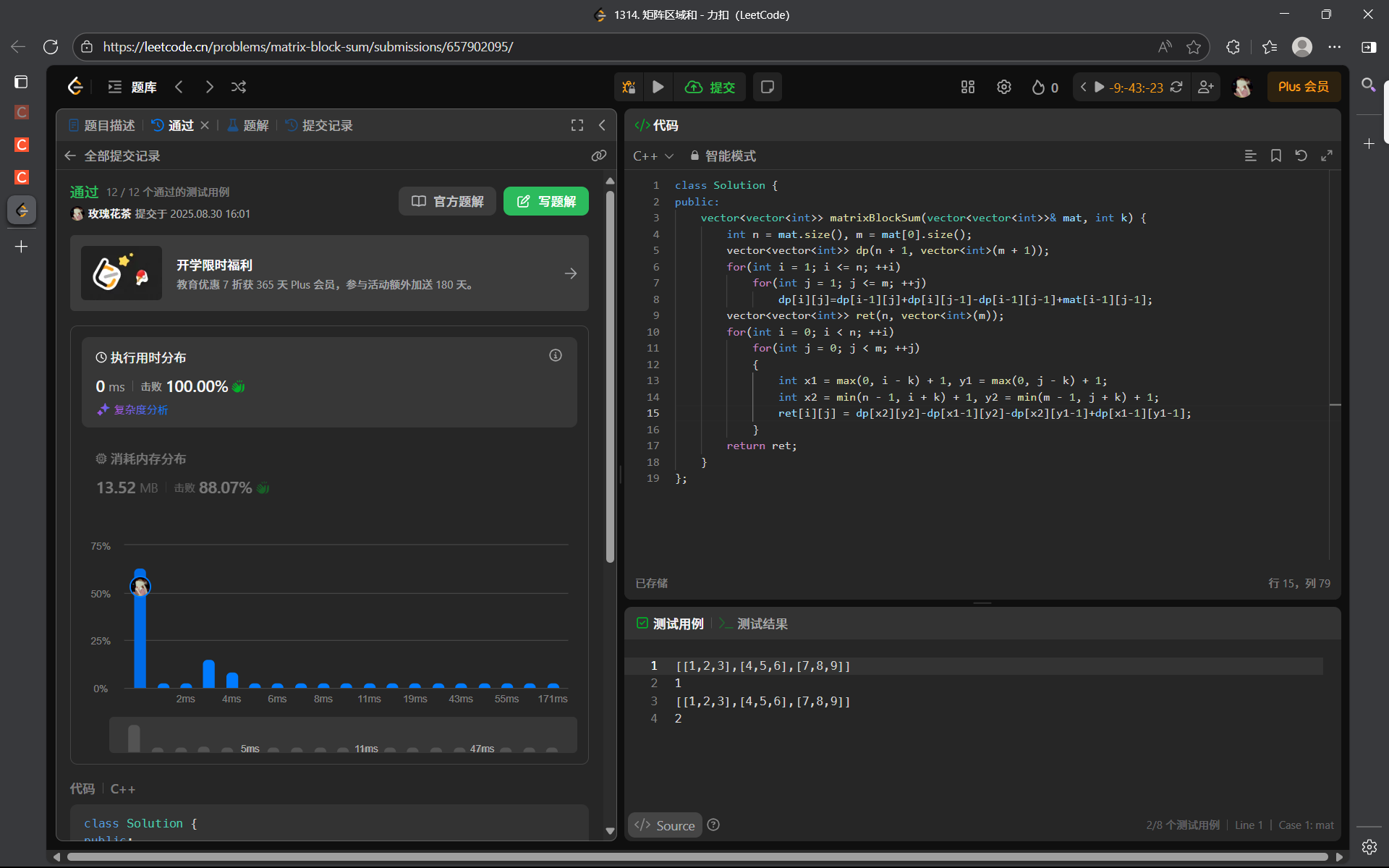
1314. 矩阵区域和 - 力扣（LeetCode）

解法：

算法思路：

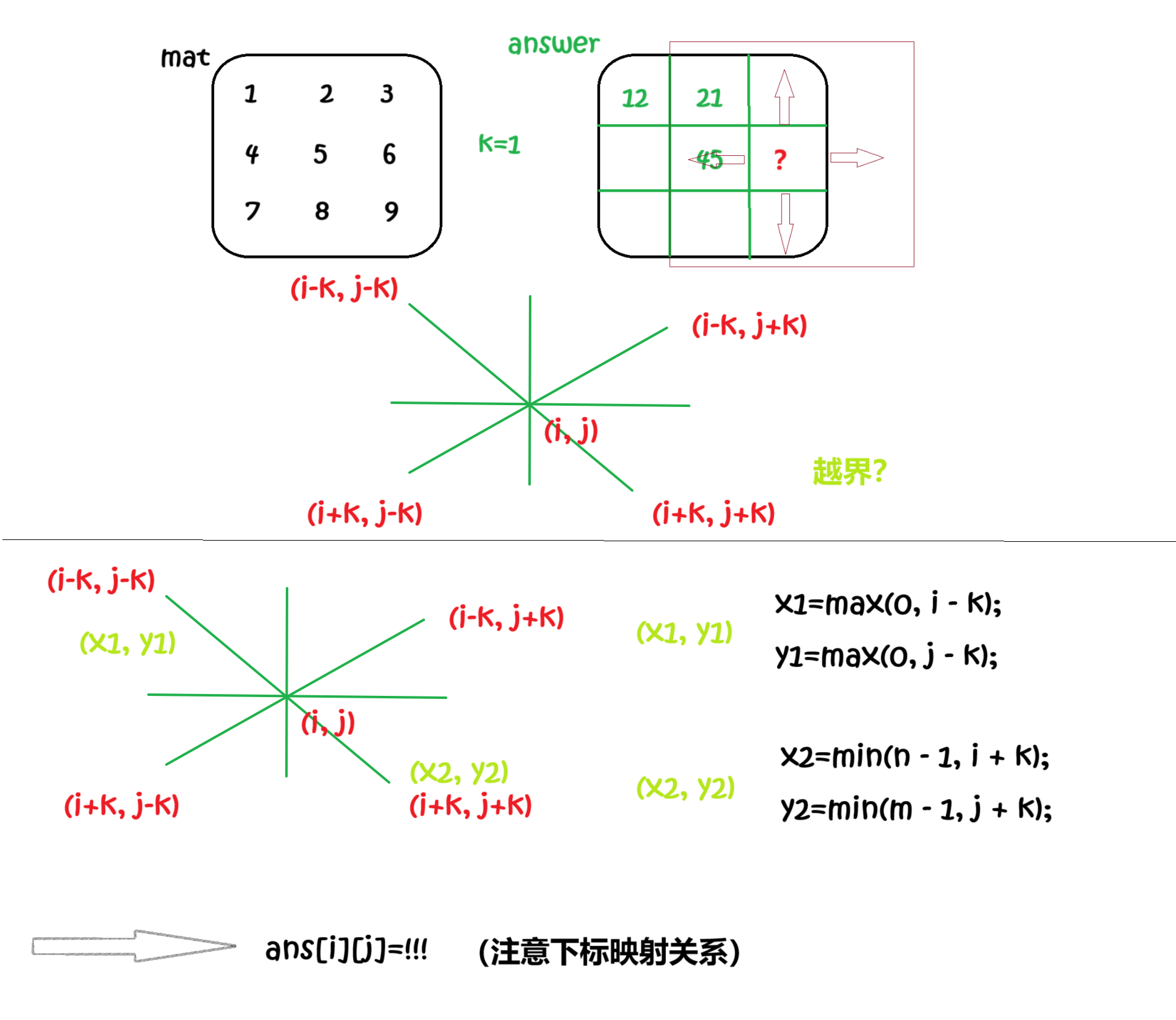
二维前缀和的简单应用题，关键就是我们在填写结果矩阵的时候，要找到原矩阵对应区域的「左上角」以及「右下角」的坐标（推荐大家画图）

• 左上角坐标：x1=i−k,y1=j−k，但是由于会「超过矩阵」的范围，因此需要对 0 取一个 max。因此修正后的坐标为：x1=max(0,i−k),y1=max(0,j−k)；

• 右下角坐标：x1=i+k,y1=j+k，但是由于会「超过矩阵」的范围，因此需要对 m−1，以及 n−1 取一个 min。因此修正后的坐标为：x2=min(m−1,i+k),y2=min(n−1,j+k)。

然后将求出来的坐标代入到「二维前缀和矩阵」的计算公式上即可~（但是要注意下标的映射关系）