[深度学习]全连接神经网络
目录
一、实验目的
二、实验环境
三、实验内容
3.1 完成解压数据集相关操作
3.2分析代码结构并运行代码查看结果
3.3修改超参数(批量大小、学习率、Epoch)并对比分析不同结果
3.4修改网络结构(隐藏层数、神经元个数)并对比分析不同结果
四、实验小结
一、实验目的
- 了解python语法
- 了解全连接神经网络结构
- 调整超参数、修改网络结构并对比分析其结果
二、实验环境
Baidu 飞桨AI Studio
三、实验内容
3.1 完成解压数据集相关操作
输入以下两行命令解压数据集
(1)cd ./data/data230
(2)unzip Minst.zip
运行后结果如图1所示
图 1 解压数据集
3.2分析代码结构并运行代码查看结果
代码结构:
import torchfrom torch import nn, optimfrom torch.autograd import Variablefrom torch.utils.data import DataLoaderfrom torchvision import datasets, transformsbatch_size = 64learning_rate = 0.02class Batch_Net(nn.Module):def __init__(self, in_dim, n_hidden_1, n_hidden_2, out_dim):super(Batch_Net, self).__init__()self.layer1 = nn.Sequential(nn.Linear(in_dim, n_hidden_1), nn.BatchNorm1d(n_hidden_1), nn.ReLU(True))self.layer2 = nn.Sequential(nn.Linear(n_hidden_1, n_hidden_2), nn.BatchNorm1d(n_hidden_2), nn.ReLU(True))self.layer3 = nn.Sequential(nn.Linear(n_hidden_2, out_dim))def forward(self, x):x = self.layer1(x)x = self.layer2(x)x = self.layer3(x)return xdata_tf = transforms.Compose([transforms.ToTensor(),transforms.Normalize([0.5], [0.5])])train_dataset = datasets.MNIST(root='./data/data230', train=True, transform=data_tf, download=True)test_dataset = datasets.MNIST(root='./data/data230', train=False, transform=data_tf)train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)#model = net.simpleNet(28 * 28, 300, 100, 10)# model = Activation_Net(28 * 28, 300, 100, 10)model = Batch_Net(28 * 28, 300, 100, 10)if torch.cuda.is_available():model = model.cuda()criterion = nn.CrossEntropyLoss()optimizer = optim.SGD(model.parameters(), lr=learning_rate)epoch = 0for data in train_loader:img, label = dataimg = img.view(img.size(0), -1)if torch.cuda.is_available():img = img.cuda()label = label.cuda()else:img = Variable(img)label = Variable(label)out = model(img)loss = criterion(out, label)print_loss = loss.data.item()optimizer.zero_grad()loss.backward()optimizer.step()epoch+=1if epoch%100 == 0:print('epoch: {}, loss: {:.4}'.format(epoch, loss.data.item()))model.eval()eval_loss = 0eval_acc = 0for data in test_loader:img, label = dataimg = img.view(img.size(0), -1)if torch.cuda.is_available():img = img.cuda()label = label.cuda()out = model(img)loss = criterion(out, label)eval_loss += loss.data.item()*label.size(0)_, pred = torch.max(out, 1)num_correct = (pred == label).sum()eval_acc += num_correct.item()print('Test Loss: {:.6f}, Acc: {:.6f}'.format(eval_loss / (len(test_dataset)),eval_acc / (len(test_dataset))))代码分析:
代码实现了通过使用批标准化的神经网络模型对MNIST数据集进行分类。
1.首先定义一些模型中会用到的超参数,在实验中设置批量大小(batch_size)为64,学习率(learning_rate)为0.02
2.定义Batch_Net神经网络类继承自torch库的nn.Module。
(1)定义的初始化函数_init_接收输入维度(in_dim)、两个隐藏层神经元数量(n_hidden_1和n_hidden_2)和输出维度(out_dim)作为参数,定义第一层和第二层网络结构,包括线性变换、批标准化和ReLU激活函数,第三层网络结构只包括线性变换。
(2)定义的forward前向传播函数接受输入x,依次经过三层网络结构处理后返回处理结果。
3.将数据进行预处理。包括使用transforms.ToTensor()将图片转换成PyTorch中处理的对象Tensor,并进行标准化操作,通过transforms.Normalize()做归一化(减均值,再除以标准差)操作,通过transforms.Compose()函数组合各种预处理的操作。
4.下载并加载MNIST训练数据(train_dataset)以及测试数据(test_dataset);创建数据加载器,用于批量加载训练数据(train_loader)和测试数据(test_loader)。
5.选择训练的模型,实验中选择Batch_Net模型,判断GPU是否可用,如果GPU可用,则将模型放到GPU上运行。在定义损失函数(criterion)和优化器(optimizer),损失函数使用交叉熵损失,优化器使用随机梯度下降优化器。
6.开始训练模型,遍历训练数据,通过img.view(img.size(0), -1)将图像数据调整为一维张量,以便与模型的输入匹配。计算损失值(loss)并进行反向传播和参数更新,每100个epoch打印一次训练损失,最后评估模型在测试集上的性能,计算并打印总损失(将损失值乘以当前批次的样本数量,累加到eval_loss中)和准确率(eval_acc)。
运行代码后的结果如图所示:

图 2 批量大小=64,学习率=0.02,Epoch次数=100
3.3修改超参数(批量大小、学习率、Epoch)并对比分析不同结果
1.当只修改批量大小batch_size时(学习率=0.02,Epoch次数=100)
(1)batch_size=16,结果如图3所示
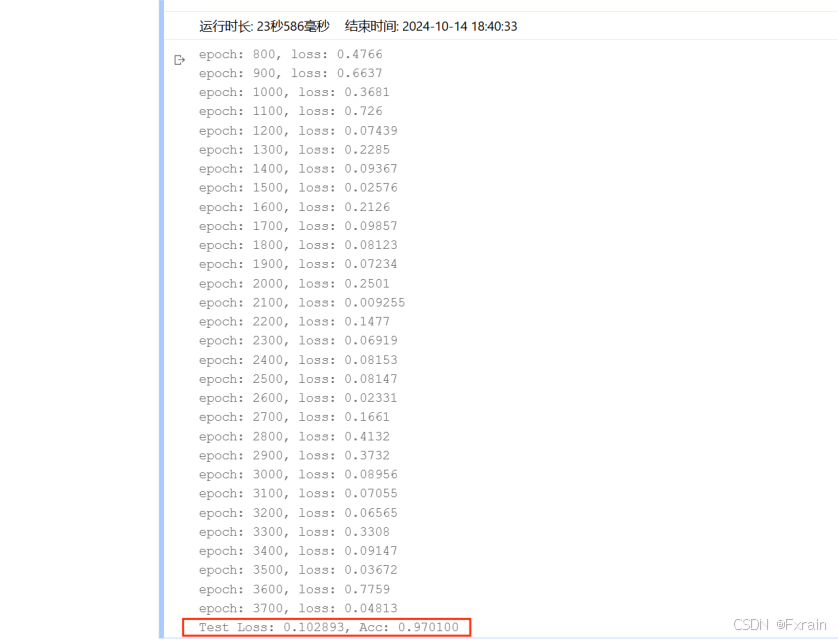
图 3
(2)batch_size=64,结果如图4所示

图 4
(3)batch_size=128,结果如图5所示

图 5
对比总结:增大batch_size后,数据的处理速度加快,运行时间变短,跑完一次 epoch(全数据集)所迭代的次数减少。
2.当只修改学习率learning_rate时(批量大小=64,Epoch次数=100)
(1)learning_rate=0.005,结果如图6所示。

图 6
(2)learning_rate=0.02,结果如图7所示。

图 7
(3)learning_rate=0.1,结果如图8所示。

图 8
(4)learning_rate=0.4,结果如图9所示。

图 9
对比总结:当学习率适当增大时可能会有助于降低损失函数,提高模型的精确度,但是当学习率超出一定范围则会降低模型的精确率。
3.当只修改Epoch次数时(批量大小=64,学习率=0.02)
(1)Epoch=50,结果如图10所示。

图 10
(2)Epoch=100,结果如图11所示。

图 11
(3)Epoch=200,结果如图12所示。

图 12
对比总结:不同Epoch次数导致损失函数不同、模型的准确率有所差别。
3.4修改网络结构(隐藏层数、神经元个数)并对比分析不同结果
1.修改神经网络的隐藏层数
(1)隐藏层数为两层时的结果(n_hidden_1、n_hidden_2),结果如图13所示。

图 13
(2)隐藏层数为三层时的结果(n_hidden_1、n_hidden_2、n_hidden_3),结果如图14所示。
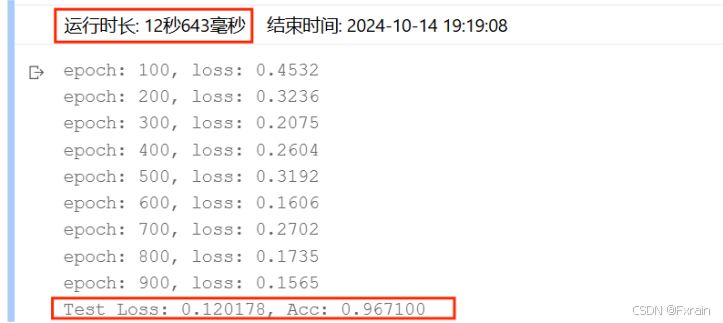
图 14
对比结果:可以看到,增加隐藏层个数后,运行时间增加,损失函数有所降低,三层隐藏层网络结构的模型准确率较高于两层隐藏层模型的准确率。
2.修改神经元个数(这里基于三层隐藏层数进行实验)
(1)神经元个数参数设定为model = Batch_Net(28 * 28, 300, 200,100, 10),结果如图15所示。

图 15
(2)神经元个数参数设定为model = Batch_Net(28 * 28, 400, 300,200, 10),结果如图16所示。

图 16
(3)神经元个数参数设定为model = Batch_Net(28 * 28, 200, 100,50, 10),结果如图17所示。

图 17
四、实验小结
超参数是在训练神经网络之前设置的,而不是通过训练过程中学习得出的。常见的超参数包括学习率、批量大小、隐藏层的数量、神经元的个数等等。在使用深度神经网络时,正确地调整超参数是提高模型性能的关键。
