【质数】埃氏筛法、线性筛法（欧拉筛法）

埃氏筛法

核心思想：对于任意一个大于1的整数，它的 k (k > 1) 倍是一个合数。

根据这个思想，我们可以从2开始遍历到n，遍历到每一个数字 i 时，都枚举它的 k 倍的数字，打上合数的标记。

这里可以做一个小优化，就是在枚举数字 i 的 k 倍数字时，可以从 i * i 开始枚举，因为小于 i * i 的数字都已经被枚举过了。

举个例子🌰：

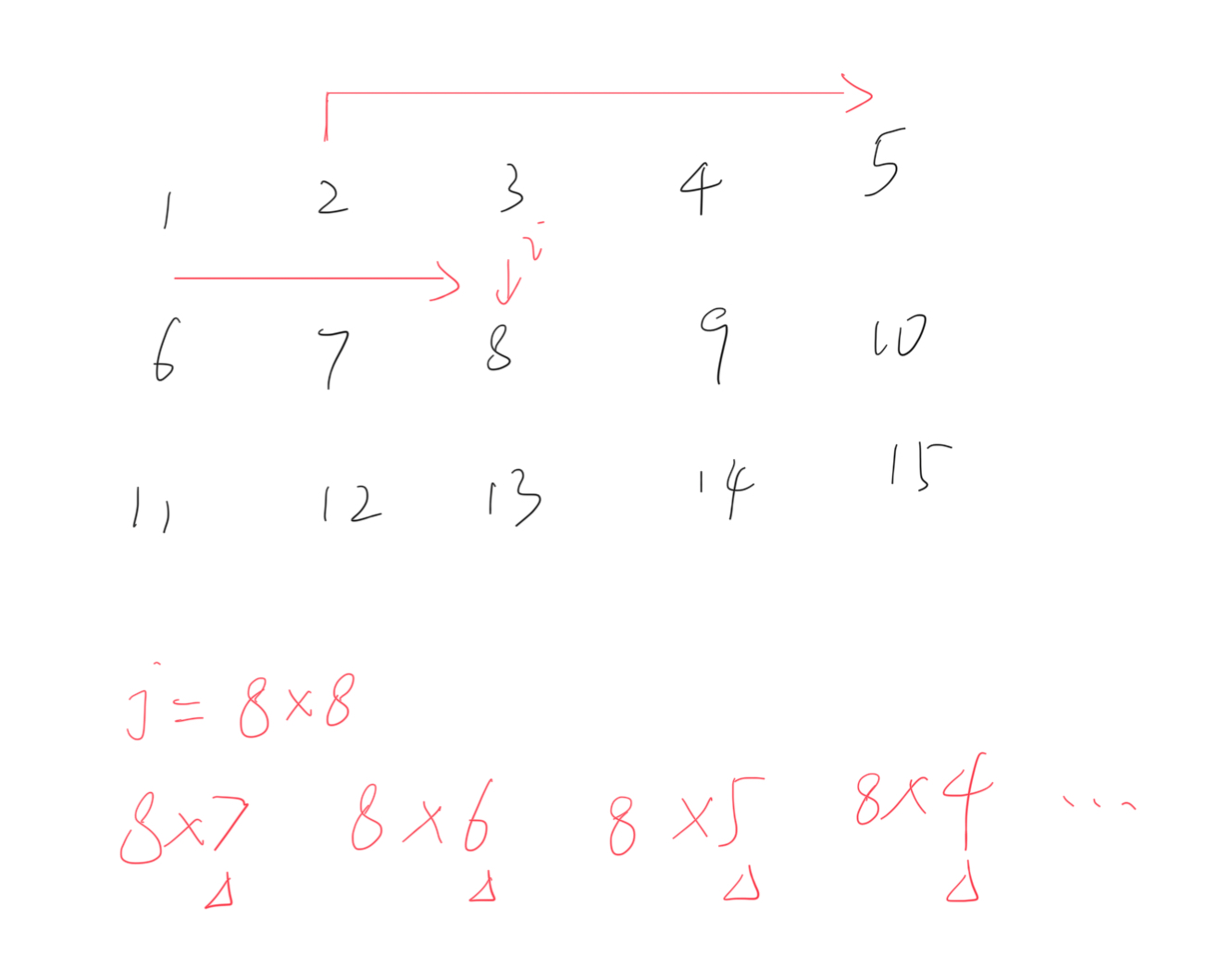
当 i 从 2 枚举到 8 的时候，现在我们要开始筛掉所有 2~n 范围内 8 的倍数，将它们标记为合数。那么现在问题来了：要从 1 * 8、2 * 8、3 * 8 开始一直枚举吗？并不需要。如图所示，我们只需要从 8 * 8 开始枚举，因为小于 8 * 8 的倍数（7 * 8 、6 * 8、5 * 8、4 * 8 …）都已经在 i 到达 8 之前枚举过了。

模板代码：

void get_prime()
{for(LL i=2;i<=n;i++) //开LL防溢出 {if(!st[i]) //是质数 {p[++cnt] = i; //将质数放入p数组for(LL j=i*i;j<=n;j+=i) //开LL 小优化：从i*i开始遍历 {st[j] = true;}}}
}

时间复杂度

O(nloglogn)
loglogn已经近似常数了，算是非常优的算法，但是埃氏筛法在标记合数的时候可能会重复多次访问同一个数字，如果我们能让每一个数字只被访问一次，那么时间复杂度就会降低到O(n)，于是我们在线性筛里要解决这个问题。

线性筛法（欧拉筛法）

核心思想：要让一个合数被它的最小质因数筛掉。

怎么实现这个想法呢？
我们从小到大遍历 2~n 的所有数字，如果遇到没被标记的数字就加入质数数组 p ，然后通过 j 遍历质数数组，将 i 从小到大依次乘上当前找到的所有质数，然后筛掉这个乘积。当 j 遍历到某个质数，i 可以整除这个质数的时候就停止当前的 i 的枚举，进入到下一个 i 的枚举。

总结：
从前往后遍历每一个 i

• 用 i 的质数倍去筛
• 遇到 i 是质数的倍数的时候就要停止

😕为什么遇到某一个质数可以整除 i 的时候就要停止呢？
简单理解就是当你遇到某一个质数，你是它的倍数的时候，这个时候筛掉的合数仍然是可以看作被这个最小质因数筛掉的。但是如果继续筛，你身上就携带了这个可以整除你的质数。

就拿图中的例子来说，遇到 9 * 3 的时候，由于 9 是 3 的倍数，于是我可以将 9 分解成 3 * 3 ，于是 9 * 3 就变成了 3 * 3 * 3(27)，这个 27 就是被它的最小质因数筛掉的，但是如果继续筛 9 * 4 ，那么 36 就是被 4 这个质数筛掉的，但是换个视角看，9 * 4 可以分解为 3 * 3 * 4 ，最小的质数是 3，所以 36 实际上在将来是应该要被它的最小质因数 3 筛掉的，即 12 * 3 的时候筛掉这个 36。这样以来就导致了重复的访问。
模板代码

void get_prime()
{for(LL i=2;i<=n;i++) //LL是防止 i * p[j]的时候溢出 {if(!st[i]) p[++cnt] = i; //没有标记就是质数，加入质数的数组 for(int j=1;i * p[j] <= n;j++) //j是p数组的下标，依次筛去i的质数倍 {st[i * p[j]] = true; //合数打上标记，筛掉 if(i % p[j] == 0) break; //如果i是该质数的倍数就停止 }}
}