人工智能-模型评价与优化(过拟合与欠拟合，数据分离与混淆矩阵，模型优化，实战)

欠拟合与过拟合

模型不合适，导致其无法与数据实现有效预测

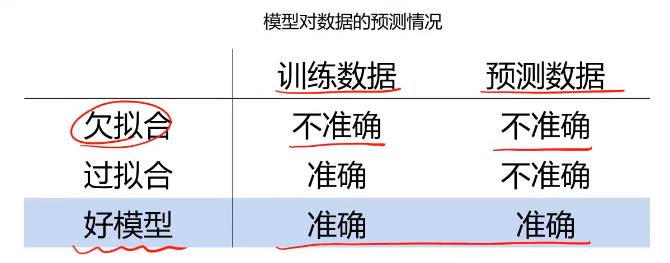
欠拟合可以通过观察训练数据及时发现，通过优化模型结果解决
过拟合的原因：
1、模型结构过于复杂（维度太高）
2、使用了过多属性，模型训练时包含了干扰项信息
过拟合的解决方法：
1、简化模型（使用低阶模型，如线性模型）
2、数据预处理，保留主成分信息（PCA处理）
3、训练时增加正则化项（regularization）



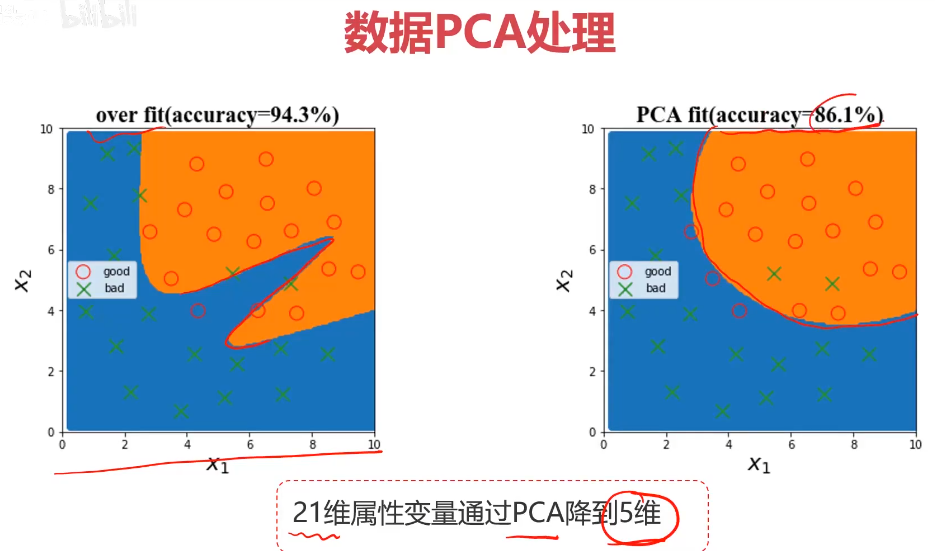
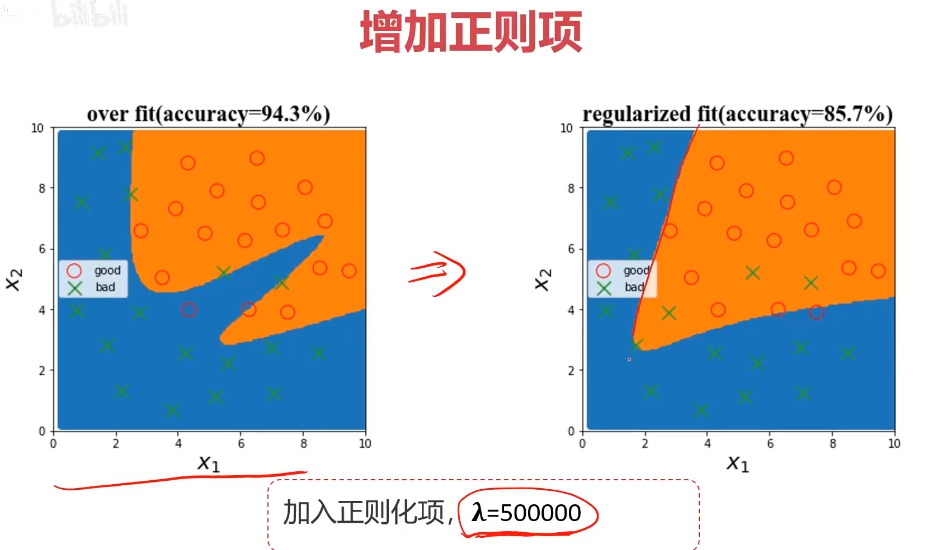
正则项越大，参数的数值就会变小，对应的值，影响就会变小，就更平滑。

数据分离与混淆矩阵

数据分离：

建立模型的意义，不在于对训练数据做出准确预测，而在于对新数据的准确预测
对全数据进行数据分离，部分用于训练，部分用于预测。（训练集，测试集）
混淆矩阵：

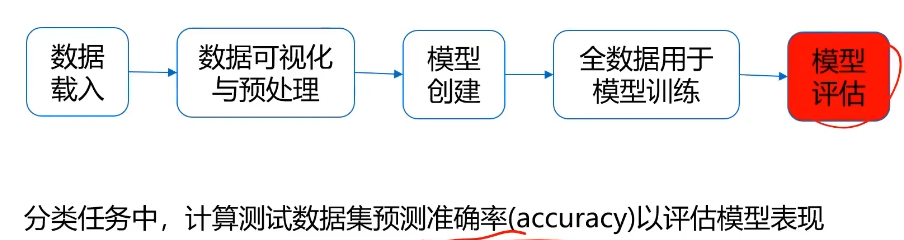
局限性：无法真实反映模型针对各个分类的预测准确度
例子：900个1，100个0的数据集。
模型1：850个1，50个0，准确率90%
模型2：全都是1，准确率90%。（空准确率）
准确率可以方便用于衡量模型的整体预测效果，但无法反应细节信息，具体表现在：
1、没有体现数据预测的实际分布情况
2、没有体现模型错误预测的类型

混淆矩阵

混淆矩阵，又称为误差矩阵，用于衡量分类算法的准确程度


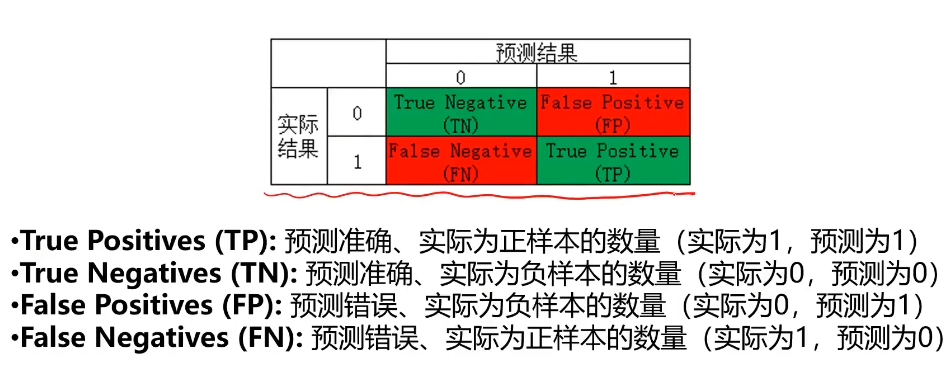
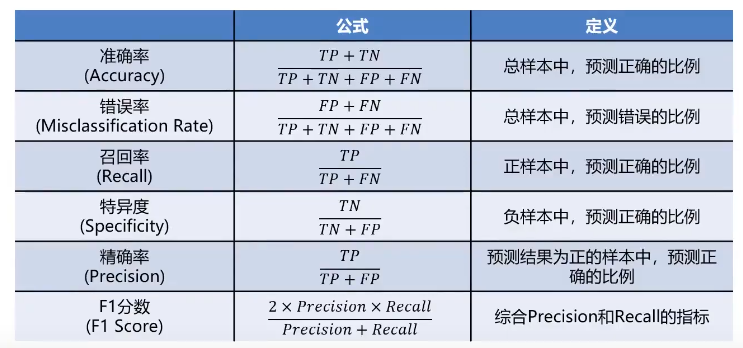
混淆矩阵指标特点：
1、分类任务中，相比单一的预测准确率，混淆矩阵提供了更全面的模型评估信息
2、通过混淆矩阵，我们可以计算出多样的模型表现衡量指标，从而更好地选择模型

哪个衡量指标更关键？
1、衡量指标的选择取决于应用场景
2、垃圾邮件检测，需精确率和召回率（希望垃圾邮箱尽可能多被判断出来）
3、异常交易检测，还需要特异度

模型优化

任务：根据检测数据x1,x2及其标签，判断x1=6,x2=4时所属类别
问题1：用什么算法？
如：逻辑回归，KNN，决策树，神经网络
问题2：具体算法的核心结构或参数如何选择？
如：逻辑回归边界函数用什么？线性、多项式?
KNN的核心参数n_neighbors取多少合适？
问题3：模型表现不佳，怎么办？
如：训练数据准确率太低，测试数据准确率下降明显，召回率/特异度/精确率低

数据的重要性：

数据的质量决定模型表现的上限！

Always check:
1、数据属性的一样，是否为无关数据
2、不同属性数据的数量级差异性如何
3、是否有异常数据
4、采集数据的方法是否合理，采集到的数据是否有代表性
5、对于标签结果，要确保标签判定规则的一致性（统一标准）

Always try:
1、删除不必要的属性
2、数据预处理：归一化、标准化
3、确定是否保留或过滤掉异常数据
4、尝试不同的模型，对比模型表现

Benefits：
1、减少过拟合，节约运算时间
2、平衡数据影响，加快训练收敛
3、提高鲁棒性
4、帮助确定更合适的模型

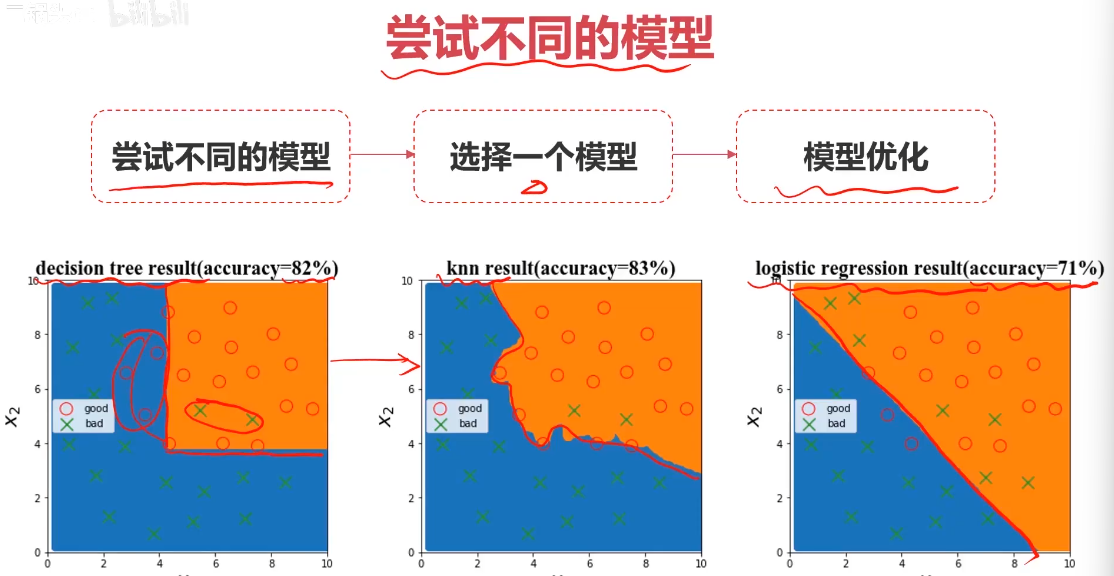
模型优化的目的：
在确定模型后，如何让模型表现更好
三方面：数据，模型核心参数，正则化
尝试以下方法：
1、遍历核心参数组合，评估对应模型表现（比如回归边界函数考虑多项式、KNN尝试不同的n_neighbors值）
2、扩大数据样本
3、增加或减少数据属性
4、对数据进行降维处理
5、对模型进行正则化处理，调整正则项 $入$ 的数值
模型关键参数选择：
选择使用KNN模型，尝试不同n_neighbors值对结果的影响

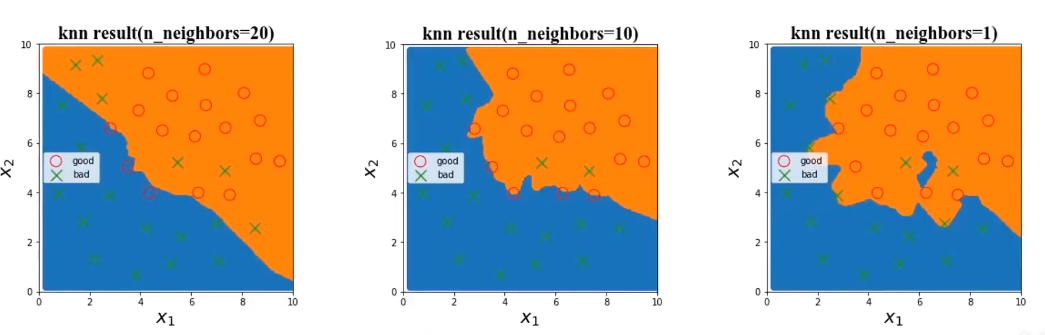
1、KNN模型中，模型复杂度由n_neighbors值决定
2、n_neighbors值越小，模型复杂度越高

训练数据集准确率随着模型复杂而提高
测试数据集准确率在模型过于简单或过于复杂的情况时下降

实战

实战（1)：酶活性预测：

生成新数据并用于预测：

X_range = np.linspace(40,90,300).reshape(-1,1)
y_range_predict = lr1.predict(X_range)

linspace 函数的作用：
生成40~90的300个数据
reshape 函数的作用：
-1：表示让 NumPy 自动计算该维度的大小。在这种情况下，-1 表示让 NumPy 自动确定行数，以确保总元素数量保持不变。
1：表示将数组的列数设置为 1。
生成多项式（二次）数据：

from sklearn.preprocessing import
PolynomialFeatures
poly2 = PolynomialFeatures(degree=2)
X_2_train = poly2.fit_transform(X_train)
X_2_test = poly2.transform(X_test)

PolynomialFeatures(degree=2)生成最高项为2的多项式

实战（2）：质量好坏预测

数据分离：

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=4,test_size=0.4)

test_size=0.4:划分训练集和测试集的比例，训练6，测试4.

生成决策区域数据：

xx, yy = np.meshgrid(np.arange(0,10,0.05),np.arange(0,10,0.05))
x_range = np.c_[xx.ravel(),yy.ravel()]
y_range_predict = knn.predict(x_range)

np.c_ 的作用:
np.c_ 是 NumPy 中的一个工具，用于按列连接数组。
np.c_[xx.ravel(), yy.ravel()] 的结果是一个二维数组，其中每行是一个坐标点 (x,y)。

可视化决策区域：

bad_knn = plt.scatter(x_range[:,0][y_range_predict==0],x_range[:,1][y_range_predict==0])
good_knn = plt.scatter(x_range[:,0][y_range_predict==1],x_range[:,1][y_range_predict==1])

计算混淆矩阵：

from sklearn.metrics import confusion matrix
cm = confusion_matrix(y_test,y_test_predict)
TP = cm[1,1]
TN = cm[0,0]
FP = cm[0,1]
FN = cm[1,0]

计算召回率、特异度、精确率、F1分数：
recall = TP/(TP+FN)
specificity = TN/(TN+FP)
precision = TP/(TP+FP)
f1 = 2 * precision * recall / (precision+recall)

实战（1）：酶活性预测

1. 基于T-R-train.csv数据，建立线性回归模型，计算其在T-R-test.csv数据上的r2分数，可视化模型预测结果
2. 加入多项式特征（2次，5次），建立回归模型
3. 计算多项式回归模型对测试数据进行预测的r2分数，判断哪个模型预测更准确
4. 可视化多项式回归模型数据预测结果，判断哪个模型预测更准确

#load the data
import pandas as pd
import numpy as np
data_train = pd.read('T-R-train.csv)

#define X_train and y_train
X_train = data_train.loc[:,'T']
y_train = data_train.loc[:,'rate']

#visual the data
%matplotlib inline
from matplotlib import pyplot as plt
fig1 = plt.figure(figsize=(10,10))
plt.scatter(X_train, y_train)
plt.title('raw data')
plt.xlabel('temperatrue')
plt.ylabel('rate')
plt.show()

X_train = np.array(X_train).reshape(-1,1)

#linear regression model prediction
from sklearn.linear_model import LinearRegression
lr1 = LinearRegression()
lr1.fit(X_train, y_train)

#load the test data
data_test = pd.read_csv('T-R-test.csv')
X_test = data_test.loc[:,'T']
y_test = data_test.loc[:,'rate']

X_test = np.array(X_test).reshape(-1,1)

#make prediction on the training and testing data
y_train_predict = lr1.predict(X_train)
y_test_predict = lr1.predict(X_test)
from sklearn.metrics import r2_score
r2_train = r2_score(y_train, y_train_predict)
r2_test = r2_score(y_test, y_test_predict)
print('training r2:', r2_train)
print('test r2:', r2_test)

#generate new data
X_range = np.linspace(40, 90, 300).reshape(-1,1)
y_range_predict = lr1.predict(X_range)

#visual the data 
fig2 = plt.figure(figsize=(10,10))
plt.plot(X_range , y_range_predict )
plt.scatter(X_train, y_train)
plt.title('predoction data')
plt.xlabel('temperatrue')
plt.ylabel('rate')
plt.show()

#多项式模型
#generate new features
from sklearn.preprocessing import PolynomialFeatures
poly2 = PolynomialFeatures(degree=2)
X_2_train = poly2.fit_transform(X_train)
X_2_test = poly2.transform(X_test)
print(X_2_train)

lr2 = LinearRegression()
lr2.fit(X_2_train, y_train)
y_2_train_predict = lr2.predict(X_2_train)
y_2_test_predict = lr2.predict(X_2_test) 
r2_2_train = r2_score(y_train, y_2_train_predict)
r2_2_test = r2_score(y_test, y_2_test_predict)
print('training r2_2:', r2_train)
print('test r2_2:', r2_test)

#generate new data
X_2_range = np.linspace(40, 90, 300).reshape(-1,1)
X_2_range = poly2.transform(X_2_range)
y_2_range_predict = lr2	.predict(X_2_range)

#visual the data 
fig3 = plt.figure(figsize=(10,10))
plt.plot(X_range , y_2_range_predict )
plt.scatter(X_train, y_train)
plt.scatter(X_test, y_test)
plt.title('polynomial prediction result(2)')
plt.xlabel('temperatrue')
plt.ylabel('rate')
plt.show()

实战（2）：质量好坏预测

1、基于data_class_raw.csv数据，根据高斯分布概率密度函数，寻找异常点并剔除
2、基于data_class_processed.csv数据，进行PCA处理，确定重要数据维度及成分
3、完成数据分离，数据分离参数：random_state=4,test_size=0.4
4、建立KNN模型完成分类，n_neighbors取10，计算分类准确率，可视化分类边界
5、计算测试数据集对应的混淆矩阵，计算准确率、召回率、特异度、精确率、F1分数
6、尝试不同的n_neighbors(1-20),计算其在训练数据集、测试数据集上的准确率并作图

#load the data
import pandas as pd
import numpy as np
data = pd.read_csv('data_class_raw.csv')
#data.head()

#define X and y
X = data.drop(['y'],axis=1)
y = data.loc[:,'y']

#visual the data
%matplotlib inline
from matplotlib import pyplot as plt
fig1 = plt.figure(figsize=(5,5))
bad = plt.scatter(X.loc[:,'x1'][y==0], X.loc[:,'x2'][y==0])
good = plt.scatter(X.loc[:,'x1'][y==1], X.loc[:,'x2'][y==1])
plt.legend((good, bad),('good', 'bad'))
plt.title('raw data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()

#anomay detection
from sklearn.covariance import EllipticEnvelope
ad_model = EllipticEnvelope(contamination=0.02)
ad_model.fit(X[y==0])
y_predict_bad = ad_model.predict(X[y==0])
print(y_predict_bad)

fig2 = plt.figure(figsize=(5,5))
bad = plt.scatter(X.loc[:,'x1'][y==0], X.loc[:,'x2'][y==0])
good = plt.scatter(X.loc[:,'x1'][y==1], X.loc[:,'x2'][y==1])
plt.scatter(X.loc[:,'x1'][y==0][y_predict_bad ==-1], X.loc[:,'x2'][y==0][y_predict_bad==-1],marker='x',s=150)
plt.legend((good, bad),('good', 'bad'))
plt.title('raw data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()

#load the data
data = pd.read_csv('data_class_processed.csv')
data.head()
#define X and y
X = data.drop(['y'],axis=1)
y = data.loc[:,'y']
#pca
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
X_norm = StandardScaler().fit_transform(X)
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X_norm)
var_ratio = pca.explained_variance_ratio_
print(var_ratio)
fig4 = plt.figure(figsize=(5,5))
plt.bar([1,2],var_ratio)
plt.show()

#train and test split: random_state=4, test_size=0.4
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=4,test_size=0.4)
print(X_train.shape,X_test.shape,X.shape)

#knn model
from sklearn.neighbors import KNeighborsClassifier
knn_10 = KNeighborsClassifier(n_neighbors=10)
knn_10.fit(X_train,y_train)
y_train_predict = knn_10.predict(X_train)
y_test_predict = knn_10.predict(X_test)
#calculate the accuracy
from sklearn.metrics import accuracy_score
accuracy_train = accuracy_score(y_train, y_train_predict)
accuracy_test = accuracy_score(y_test, y_test_predict)
print("training accuracy:", accuracy_train)
print("testing accuracy:", accuracy_test)
#visualize the knn result and baundary
xx, yy = np.meshgrid(np.arrange(0,10,0.05),np.arrange(0,10,0.05))
x_range = np.c_[xx.ravel(),yy.ravel()]
#print(x_range.shape)
y_range_predict = knn_10.predict(x_range)
fig4 = plt.figure(figsize=(10,10))
knn_bad = plt.scatter(x_range.loc[:,0][y_range_predict ==0], x_range.loc[:,1][y_range_predict ==0])
knn_good = plt.scatter(x_range.loc[:,0][y_range_predict ==1], x_range.loc[:,1][y_range_predict ==1])
bad = plt.scatter(X.loc[:,'x1'][y==0], X.loc[:,'x2'][y==0])
good = plt.scatter(X.loc[:,'x1'][y==1], X.loc[:,'x2'][y==1])
plt.legend((good, bad),('good', 'bad'))
plt.title('raw data')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_test_predict)
#print(cm)
TP = cm[1,1]
TN = cm[0,0]
FP = cm[0,1]
FN = cm[1,0]
#print(TP,TN,FP,FN) 
accuracy = (TP+TN)/(TP+TN+FP+FN)
recall = TP/(TP+FN)
specificity = TN/(TN+FP)
precision = TP/(TP+FP)
f1 = 2*precision*recall/(precision+recall)

#try different k and calculate the accuracy for each
n = [i for i in range(1,21)]
accuracy_train = []
accuracy_test = []
for i in n:knn = KNeighborsClassifier(n_neighbors=i)knn.fit(X_train,y_train)y_train_predict = knn.predict(X_train)y_test_predict = knn.predict(X_test)accuracy_train_i = accuracy_score(y_train,y_train_predict)accuracy_test_i = accuracy_score(y_test,y_test_predict)accuracy_train.append(accuracy_train_i)accuracy_test.appedn(accuracy_test_i)
print(accuracy_train,accuracy_test)
#visual
fig5 = plt.figure(figsize=(12,5))
plt.subplot(121)
plt.plot(n, accuracy_train,marker='0')
plt.title('training accuracy vs n_neighbors')
plt.xlabel('n_neighbors')
plt.tlabel('accuracy')
plt.subplot(122)
plt.plot(n, accuracy_test,marker='0')
plt.title('testing accuracy vs n_neighbors')
plt.xlabel('n_neighbors')
plt.tlabel('accuracy')
plt.show()