八数码难题的多种解法
蔡自兴老师的《人工智能及其应用》这本书的第3章里面讲解了很多种搜索方法,因为看的不是很懂,所以网上就找了资源来帮助理解。
为了帮助各位更好的理解,在此,仅以八数码难题为实例来解释说明。
#首先描述下八数码难题

一、宽度优先搜索
1. 宽度优先搜索
它是从根节点(起始节点)开始,按层进行搜索,也就是按层来扩展节点。所谓按层扩展,就是前一层的节点扩展完毕后才进行下一层节点的扩展,直到得到目标节点为止。这种搜索方式的优点是,只要存在有任何解答的话,它能保证最终找到由起始节点到目标节点的最短路径的解,但它的缺点是往往搜索过程很长。
 宽度优先搜索的性质
宽度优先搜索的性质
- 当问题有解时,一定能找到解
- 当问题为单位耗散值,且问题有解时,一定能找到最优解
- 方法与问题无关,具有通用性
- 效率较低
- 属于图搜索方法
二、深度优先搜索
它是从根节点开始,首先扩展最新产生的节点,即沿着搜索树的深度发展下去,一直到没有后继结点处时再返回,换一条路径走下去。就是在搜索树的每一层始终先只扩展一个子节点,不断地向纵深前进直到不能再前进(到达叶子节点或受到深度限制)时,才从当前节点返回到上一级节点,沿另一方向又继续前进。这种方法的搜索树是从树根开始一枝一枝逐渐形成的。
由于一个有解的问题树可能含有无穷分枝,深度优先搜索如果误入无穷分枝(即深度无限),则不可能找到目标节点。为了避免这种情况的出现,在实施这一方法时,定出一个深度界限,在搜索达到这一深度界限而且尚未找到目标时,即返回重找,所以,深度优先搜索策略是不完备的。另外,应用此策略得到的解不一定是最佳解(最短路径)。

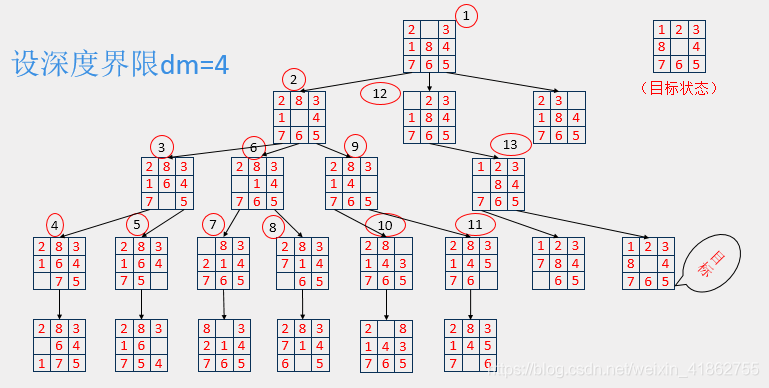
深度优先搜索的性质
- 一般不能保证找到最优解
- 当深度限制不合理时,可能找不到解,可以将算法改为可变深度限制
- 最坏情况时,搜索空间等同于穷举
- 与回溯法的差别:图搜索
- 是一个通用的与问题无关的方法
**
三 启发式搜索
**
1 有序搜索(A算法)
评价函数:f(n) = g(n) + h(n) (其中n是被评价的节点)
g*(n) :表示从初始节点s到节点n 的最短路径的耗散值。
h*(n):表示从节点n到目标节点g的最短路径的耗散值。
f*(n) =g*(n)+h*(n):表示从初始节点s经过节点n到目标节点g的最短路径的耗散值。
而f(n)、g(n)和h(n)则分别表示是对f*(n)、g*(n)和h*(n)三个函数值的估计值,是一种预测。
A算法就是利用这种预测,来达到有效搜索的目的。它每次按照f(n)值的大小对 OPEN表中的元素进行排序,f值小的节点放在前面,而f值的大的节点则被放在OPEN表的后面,这样每次扩展节点时,总是选择当前f值最小的节点来优先扩展。
有序搜索算法框图

 2 A*搜索算法
2 A*搜索算法
在图搜索过程中,如果第8步的重排OPEN表是依据f(n)=g(n)+h(n)进行的,则称该过程为A算法。在A算法中,如果对所有的n存在h(n)≤h*(n),则称h(n)为h*(n)的下界,它表示某种偏于保守的估计。采用h*(n)的下界h(n)为启发函数的A算法,称为A算法。当h=0时,A算法就变为有序搜索算法。
在A算法中,如果满足条件:
(1): g(n)是对g*(n)的估计,且g(n)>0;
(2) :h(n)是h*(n)的下界,即对任意节点n均有0≤h(n)≤h*(n),则A算法称为A*算法。
A*算法框图


注:
在八数码难题中, 令估价函数 f(n)=d(n)+p(n) ,启发函数h(n)=p(n),p(n)为不在位的棋子与其目标位置的距离之和,则有p(n)≤h*(n),满足A算法的限制条件。
w(n)表示不在位的棋子数,不够贴切,错误选用节点加以扩展。 更接近于h(n)的h(n),其值是节点n与目标状态节点相比较,每个错位棋子在假设不受阻拦的情况下,移动到目标状态相应位置所需走步的总和。(n)比w(n)更接近于h*(n),因为p(n)不仅考虑了错位因素,还考虑了错位的距离(移动次数)。 说明h值越大,启发功能越强, 搜索效率越高.特别地:
(1)h(n)=h*(n) 搜索仅沿最佳路径进行, 效率最高.
(2)h(n)=0 无启发信息, 盲目搜索, 效率低.
(3)h(n)>h*(n)
在此特别感谢 https://wenku.baidu.com/view/4e2c68ea64ce0508763231126edb6f1aff0071e3.html
