5.Transformer模型详解
Transformer模型
这里本人学习了清华大学马少平老师的课程,分享的是本人学习过程中所做的笔记以及感悟形成这篇博客。
马老师课程链接:https://space.bilibili.com/1000083494/upload/video
第一讲 来源背景
序列到序列问题(编码器-解码器模型)
输入中文 --> 翻译系统 --> 输出英文 (输入中文序列,输出英文单词序列)
文本描述 --> 生成视频 (描述是文字序列,视频是帧序列)
序列到序列问题可以表达出 编码器解码器模型
编码器将输入编码成中间表示,解码器将中间表示解码成输出 
RNN是编码器-解码器模型

循环神经网络存在的问题
-
词的语义由上下文中与其相关的词决定,但rnn可能把两个“苹果”当成一个意思

-
长距离依赖问题

-
rnn中词向量是固定的,静态的。比如“苹果”的词向量是固定的。但针对前面两个苹果,我们需要动态表示词向量。
Transformer模型
为了解决RNN存在的问题而提出的,本质仍然是 编码器-解码器模型

第二讲 注意力机制
注意力机制
来源于认知心理学中选择性注意现象。比如下图,我们第一时间看到的大概率是这只熊,而这里面有什么树,树的种类有哪些这是被我们忽略的。

下图
第一句话中,“苹果”需注意 “美味”,“吃了”,“非常”。
第二句话中,“苹果”需注意“用”,“联系”。


例子:中年人的平均收入

注意力机制描述


总结注意力机制计算过程


注意上述softmax右边乘的是V而不是V的转置(让softmax行向量中每个元素,乘对于的v向量)。最终结果就是依照注意力机制,对q的一个查询结果。
前面是一个查询,若查询有n个。

一个计算的例子



自注意力机制
引入注意力机制作用:为了计算一个词在一句话中它的含义,那么哪个是查询,哪个是键,哪个是值呢?实际上处理一句话中,每个词即是查询也是键也是值,自己跟自己来进行查询,这样就得到了词向量的动态表示,这种称为自注意力机制。

xi 表示一句话中第i个词的词向量,假定有n个词,词向量d维,则输入序列用n行d列矩阵X来表示。自注意力矩阵也为n行d列,第i行代表第i个词动态表示的词向量。

第三讲 多头注意力机制
多头注意力机制,一个头提取了某种语句特征,多头从不同角度提取不同的特征。

多头注意力机制基本思想
不同子空间就像,从侧面看,正面看,上面看。怎么变化到不同子空间呢?答: 设三个矩阵Wq, Wk, Wv,在让Q右乘这三个矩阵(向量右乘矩阵 表示把这个向量变化到了一个新的空间,如果维度有变化到化,就成为一个子空间)

一组变换中的一组指Wq, Wk, Wv称为一组


一次注意力机制的结果Ui为n行dh列。如何拼接,看下面例子:

- d为词向量的维度,为4 (U1,2,3 矩阵中的一行,对应一个单词的词向量)
- n为序列长度,为5
- h为几个头,为3
- dh为每个头的输出维度,为2
将Ui(i = 1,2…h)拼接成大矩阵U(n行,h乘dh列)之后呢,我们希望给U变换到n行d列。n行本身就是n行没问题(一行对于一个单词的词向量)。将U右乘Wo (h * dh行,d列)然后得到多头注意力矩阵(n行d列)

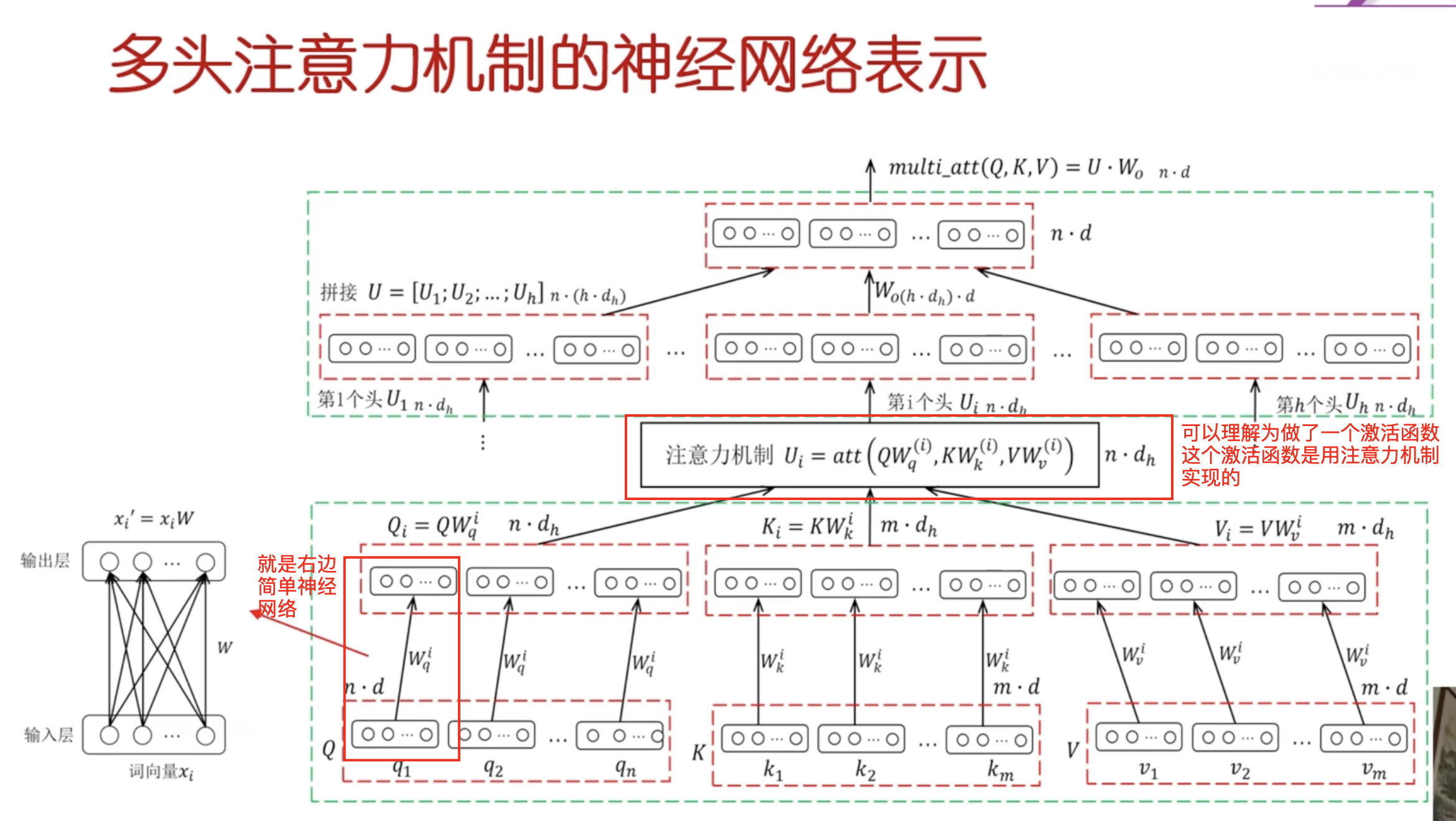
多头注意力机制的神经网络表示
多头注意力机制可以用神经网络来表示,或者是它就是一个神经网络只不过稍微有点复杂。跟神经网络的原理完全一样。
里面涉及的参数也就是那些矩阵 可以按照BP算法来训练,即当作一个神经网络来训练。
重要的概念:多头注意力机制中要先右乘一个矩阵进行空间变换(行向量右乘矩阵就是表达只有一个输入一个输出的神经网络)
第四讲 残差连接与层归一化
残差网络
残差网络图示如下,恒等映射(残差连接)是残差网络的最重要思想,注意核心计算层并不一定要用卷积也可以用别的。

残差连接的一般形式如下图

Transformer中两种残差连接
全连接神经网络的残差连接
即用全连接神经网络代替残差网络中卷积神经网络部分。
x1,x2,x3…xn中每个可以看作是一个单词的向量表示。

多头自注意力机制残差连接
即用多头自注意力机制代替残差网络中卷积神经网络部分。
x1,x2,x3…xn中每个可以看作是一个单词的向量表示。
先进行一次多头自注意力机制计算,然后每个再进行残差连接,最后得到z1,…,zn结果。

层归一化
在每个编码层,每个层对它的向量进行层归一化处理。
用来解决内部协变量偏移问题(ICS),在神经网络中当层多了后普遍存在的问题。
如何解决该问题?归一化处理,使得数据分布具有相同的均值和均方差。针对不同问题从不同角度构成了不同的归一化方法。
下图中的1向量,与zi同维,每个元素都为1。
hi分母加个很小的量防止分母为0。
这样处理后,我们可以得到hi均值为0,均方差为1,这就叫层归一化。

层归一化存在的问题与解决
绝大部分数据落入线形区域,对神经网络性能有影响

解决方法1:增加平移和缩放,平移和缩放这两个参数当作学习的参数通过训练来学习。
解决方法2: 均方根层归一化方法,是解决方法1中均值和平移量均为0时的特例。经过试验,非常有效。

第五讲 Transformer的编码器
结构示意如下图

编码器的输入层
输入层中引入了位置信息即位置向量,将位置用向量来表示

将词向量与位置向量相加得到含有位置信息的词向量

输入层矩阵表示
X是输入序列,其每一行是一个词向量,若X有n行则说明输入序列由n个单词组成

编码器的编码层
编码层的输出是对该编码层输入的编码表示

编码层具体如何来编码的呢?
step1 对编码层的输入进行多头自注意力机制计算,然后进行残差连接将编码层的输入与自注意力机制计算的结果求和。并对结果进行层归一化。
step2 对step1结果进行全连接神经网络计算,然后进行残差连接求和,最后对结果进行层归一化得到编码层的输出结果。

每个编码层结构完全一样,只不过输入输出不一样。编码层从浅到深,从对语法编码到对语义编码。最后语法信息语义信息都表示在中间表示序列了,以向量来表示。

解码层后续会接着更新,欢迎追更。。。。
