RL 基础 (待补充)
注:本文仅用于自学习笔记备忘,不做任何分享和商业用途。
主要参考资料:
- 蘑菇书EasyRL
- A (Long) Peek into Reinforcement Learning | Lil'Log
第1章 强化学习基础
RL算法分类:
- Model-based: Rely on the model of the environment; either the model is known or the algorithm learns it explicitly.
- Model-free: No dependency on the model during learning.
- On-policy: Use the deterministic outcomes or samples from the target policy to train the algorithm.
- Off-policy: Training on a distribution of transitions or episodes produced by a different behavior policy rather than that produced by the target policy.
第2章 马尔可夫决策过程
强化学习(reinforcement learning,RL)讨论的问题是智能体(agent)怎么在复杂、不确定的环境(environment)中最大化它能获得的奖励。

智能体得到环境的状态后,它会采取动作,并把这个采取的动作返还给环境。环境得到智能体的动作后,它会进入下一个状态,把下一个状态传给智能体。在强化学习中,智能体与环境就是这样进行交互的,这个交互过程可以通过马尔可夫决策过程来表示,所以马尔可夫决策过程是强化学习的基本框架。
2.1 马尔可夫过程
2.1.1 马尔可夫性质
如果某一个过程满足马尔可夫性质,那么未来的转移与过去的是独立的,它只取决于现在。马尔可夫性质是所有马尔可夫过程的基础。

马尔可夫过程:

2.1.2 马尔可夫链


我们可以用状态转移矩阵(state transition matrix)P 来描述状态转移

状态转移矩阵类似于条件概率(conditional probability),它表示当我们知道当前我们在状态 st时,到达下面所有状态的概率。所以它的每一行描述的是从一个节点到达所有其他节点的概率。
2.2 马尔可夫奖励过程
马尔可夫奖励过程(Markov reward process, MRP)是马尔可夫链加上奖励函数。在马尔可夫奖励过程中,状态转移矩阵和状态都与马尔可夫链一样,只是多了奖励函数(reward function)。奖励函数 R 是一个期望,表示当我们到达某一个状态的时候,可以获得多大的奖励。这里另外定义了折扣因子 γ 。如果状态数是有限的,那么 R 可以是一个向量。
2.2.1 回报与价值函数

其中,T是最终时刻,γ 是折扣因子,越往后得到的奖励,折扣越多。这说明我们更希望得到现有的奖励,对未来的奖励要打折扣。当我们有了回报之后,就可以定义状态的价值了,就是状态价值函数(state-value function)。对于马尔可夫奖励过程,状态价值函数被定义成回报的期望,即

其中,Gt 是之前定义的折扣回报(discounted return)。我们对Gt取了一个期望,期望就是从这个状态开始,我们可能获得多大的价值。所以期望也可以看成未来可能获得奖励的当前价值的表现,就是当我们进入某一个状态后,我们现在有多大的价值。
我们使用折扣因子的原因如下。第一,有些马尔可夫过程是带环的,它并不会终结,我们想避免无穷的奖励。第二,我们并不能建立完美的模拟环境的模型,我们对未来的评估不一定是准确的,我们不一定完全信任模型,因为这种不确定性,所以我们对未来的评估增加一个折扣。我们想把这个不确定性表示出来,希望尽可能快地得到奖励,而不是在未来某一个点得到奖励。第三,如果奖励是有实际价值的,我们可能更希望立刻就得到奖励,而不是后面再得到奖励(现在的钱比以后的钱更有价值)。最后,我们也更想得到即时奖励。有些时候可以把折扣因子设为 0(γ=0),我们就只关注当前的奖励。我们也可以把折扣因子设为 1(γ=1),对未来的奖励并没有打折扣,未来获得的奖励与当前获得的奖励是一样的。折扣因子可以作为强化学习智能体的一个超参数(hyperparameter)来进行调整,通过调整折扣因子,我们可以得到不同动作的智能体。
在马尔可夫奖励过程里面,我们如何计算价值呢?如图 2.4 所示,马尔可夫奖励过程依旧是状态转移,其奖励函数可以定义为:智能体进入第一个状态 s1 的时候会得到 5 的奖励,进入第七个状态 s7 的时候会得到 10 的奖励,进入其他状态都没有奖励。我们可以用向量来表示奖励函数,即
![]()

我们对 4 步的回合(episode)(γ=0.5)来采样回报 G:

后面会介绍MC方法,以及其他方法。
2.2.2 贝尔曼方程
贝尔曼方程的推导过程如下:

贝尔曼方程就是当前状态与未来状态的迭代关系,表示当前状态的价值函数可以通过下个状态的价值函数来计算。贝尔曼方程因其提出者、动态规划创始人理查德 ⋅⋅ 贝尔曼(Richard Bellman)而得名 ,也叫作“动态规划方程”。
贝尔曼方程定义了状态之间的迭代关系,即

假设有一个马尔可夫链如图 2.5a 所示,贝尔曼方程描述的就是当前状态到未来状态的一个转移。如图 2.5b 所示,假设我们当前在 s1, 那么它只可能去到3个未来的状态:有 0.1 的概率留在它当前位置,有 0.2 的概率去到 s2 状态,有 0.7 的概率去到 s4 状态。所以我们把状态转移概率乘它未来的状态的价值,再加上它的即时奖励(immediate reward),就会得到它当前状态的价值。贝尔曼方程定义的就是当前状态与未来状态的迭代关系。

我们可以把贝尔曼方程写成矩阵的形式:
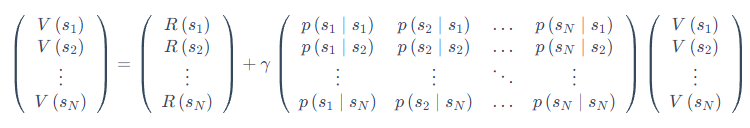

我们可以直接得到解析解(analytic solution):


