Java详解LeetCode 热题 100(20):LeetCode 48. 旋转图像(Rotate Image)详解
文章目录
- 1. 题目描述
- 2. 理解题目
- 3. 解法一:转置 + 翻转
- 3.1 思路
- 3.2 Java代码实现
- 3.3 代码详解
- 3.4 复杂度分析
- 3.5 适用场景
- 4. 解法二:四点旋转法
- 4.1 思路
- 4.2 Java代码实现
- 4.3 代码详解
- 4.4 复杂度分析
- 4.5 适用场景
- 5. 详细步骤分析与示例跟踪
- 5.1 解法一:3×3矩阵示例
- 5.2 解法二:3×3矩阵示例
- 5.3 4×4矩阵示例
- 5.4 特殊情况:奇数大小的矩阵
- 5.5 动态示意图
- 6. 常见错误与优化
- 6.1 常见错误
- 6.2 性能优化
- 7. 扩展题目与应用
- 7.1 相关矩阵变换问题
- 7.2 旋转相关的其他题目
- 8. 实际应用场景
- 9. 完整的 Java 解决方案
- 10. 总结与技巧
- 10.1 解题要点
- 10.2 学习收获
- 10.3 面试技巧
- 10.4 考察重点
- 11. 旋转矩阵的数学原理
- 11.1 线性代数视角
- 11.2 四点旋转的数学关系
- 11.3 转置和翻转的组合等价性
1. 题目描述
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
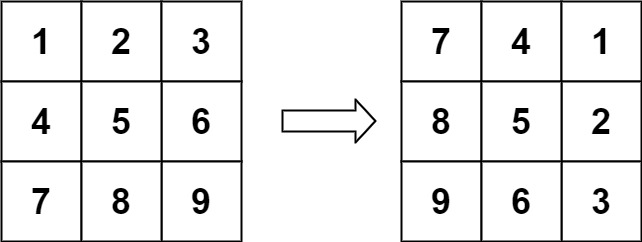
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
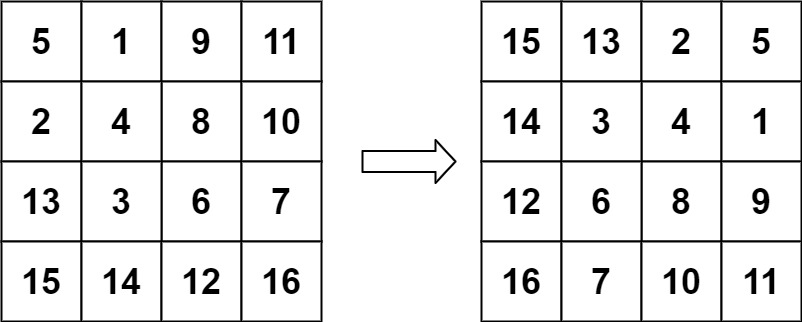
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
- n == matrix.length == matrix[i].length
- 1 <= n <= 20
- -1000 <= matrix[i][j] <= 1000
2. 理解题目
这道题要求我们将一个 n×n 的矩阵顺时针旋转 90 度,并且必须在原地修改,不能使用额外的矩阵。理解这个问题的关键在于:
- 矩阵是正方形的:这一点很重要,因为只有正方形矩阵才能原地旋转 90 度。
- 顺时针旋转 90 度:图像顺时针旋转 90 度后,原矩阵中的元素位置会发生变化。具体来说:
- 第一行元素会变成最后一列(从上到下)
- 第二行元素会变成倒数第二列(从上到下)
- 依此类推…
- 原地修改:我们不能使用额外的矩阵来存储旋转后的结果,必须直接修改输入矩阵。
如果用坐标来表示,对于一个位于 (row, col) 的元素,旋转 90 度后,它的新位置应该是 (col, n-1-row)。这种变换会形成一个循环:
(row, col) → (col, n-1-row) → (n-1-row, n-1-col) → (n-1-col, row) → (row, col)
这一循环关系是解决这个问题的关键。我们需要在不使用额外空间的情况下,利用这个关系完成矩阵的旋转。
3. 解法一:转置 + 翻转
3.1 思路
将矩阵顺时针旋转 90 度可以分解为两个简单的操作:
- 先沿对角线转置矩阵(即交换 matrix[i][j] 和 matrix[j][i])
- 再将每一行左右翻转(即交换 matrix[i][j] 和 matrix[i][n-1-j])
这种解法的优势在于操作简单,易于理解和实现。
示意图:
原始矩阵: 转置后: 左右翻转后:
1 2 3 1 4 7 7 4 1
4 5 6 -> 2 5 8 -> 8 5 2
7 8 9 3 6 9 9 6 3
3.2 Java代码实现
class Solution {public void rotate(int[][] matrix) {int n = matrix.length;// 沿对角线转置矩阵for (int i = 0; i < n; i++) {for (int j = i; j < n; j++) {// 交换matrix[i][j]和matrix[j][i]int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;}}// 左右翻转每一行for (int i = 0; i < n; i++) {for (int j = 0; j < n / 2; j++) {// 交换matrix[i][j]和matrix[i][n-1-j]int temp = matrix[i][j];matrix[i][j] = matrix[i][n - 1 - j];matrix[i][n - 1 - j] = temp;}}}
}
3.3 代码详解
让我们详细解释这个解法的每个部分:
int n = matrix.length;
- 获取矩阵的大小,由于是正方形矩阵,所以行数和列数相等,都是n。
// 沿对角线转置矩阵
for (int i = 0; i < n; i++) {for (int j = i; j < n; j++) {// 交换matrix[i][j]和matrix[j][i]int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;}
}
- 这段代码实现了矩阵的转置操作,将矩阵沿着主对角线(从左上到右下)进行翻转。
- 外层循环
i遍历每一行,内层循环j从i开始遍历,这样只处理对角线上和对角线右上方的元素。 - 通过交换
matrix[i][j]和matrix[j][i],我们实现了转置操作。 - 注意内层循环
j是从i开始的,这样可以避免重复交换。例如,当我们交换了matrix[1][2]和matrix[2][1]后,就不需要再交换matrix[2][1]和matrix[1][2]了。
// 左右翻转每一行
for (int i = 0; i < n; i++) {for (int j = 0; j < n / 2; j++) {// 交换matrix[i][j]和matrix[i][n-1-j]int temp = matrix[i][j];matrix[i][j] = matrix[i][n - 1 - j];matrix[i][n - 1 - j] = temp;}
}
- 这段代码实现了将每一行左右翻转的操作。
- 外层循环
i遍历每一行,内层循环j只需要遍历到每行的一半位置。 - 通过交换
matrix[i][j]和matrix[i][n-1-j],我们实现了左右翻转。 - 内层循环只到
n/2是因为,当我们交换了左半部分和右半部分后,整行就已经完成了翻转,无需重复交换。
通过这两步操作,我们实现了矩阵的顺时针旋转 90 度,并且是在原矩阵上直接修改的,符合题目要求。
3.4 复杂度分析
- 时间复杂度: O(n²),其中 n 是矩阵的边长。我们需要访问矩阵中的每个元素至少一次。
- 空间复杂度: O(1),我们只使用了常数额外空间。
3.5 适用场景
这种解法简单直观,易于理解和实现,适用于所有的正方形矩阵旋转情况。特别是当你需要解释矩阵旋转的原理时,这种分解为转置和翻转的方法非常有教学价值。
4. 解法二:四点旋转法
4.1 思路
另一种思路是直接模拟旋转过程,每次旋转矩阵中的4个点。我们可以从外层开始,一层一层向内处理。对于每个位置(i,j),可以找到旋转后对应的其他三个位置,然后一次性完成这四个位置的旋转。
具体来说,对于位置(i,j),旋转90度后的新位置是(j,n-1-i)。我们可以找出四个互相旋转的位置:
- (i,j) -> (j,n-1-i) -> (n-1-i,n-1-j) -> (n-1-j,i) -> (i,j)
然后,我们只需要一个临时变量就可以完成这四个位置的值旋转。
示意图:
(0,0) -> (0,2) -> (2,2) -> (2,0) -> (0,0)
(0,1) -> (1,2) -> (2,1) -> (1,0) -> (0,1)
4.2 Java代码实现
class Solution {public void rotate(int[][] matrix) {int n = matrix.length;// 从外层向内层处理,一共有 n/2 层for (int layer = 0; layer < n / 2; layer++) {// 每层需要处理的元素个数int first = layer;int last = n - 1 - layer;// 对当前层的每个元素进行旋转for (int i = first; i < last; i++) {// 存储上边的元素int temp = matrix[first][i];// 左边 -> 上边matrix[first][i] = matrix[n - 1 - i][first];// 下边 -> 左边matrix[n - 1 - i][first] = matrix[last][n - 1 - i];// 右边 -> 下边matrix[last][n - 1 - i] = matrix[i][last];// 上边(temp) -> 右边matrix[i][last] = temp;}}}
}
4.3 代码详解
让我们详细解释这个解法的每个部分:
// 从外层向内层处理,一共有 n/2 层
for (int layer = 0; layer < n / 2; layer++) {// 每层需要处理的元素个数int first = layer;int last = n - 1 - layer;// 对当前层的每个元素进行旋转for (int i = first; i < last; i++) {// 存储上边的元素int temp = matrix[first][i];// 左边 -> 上边matrix[first][i] = matrix[n - 1 - i][first];// 下边 -> 左边matrix[n - 1 - i][first] = matrix[last][n - 1 - i];// 右边 -> 下边matrix[last][n - 1 - i] = matrix[i][last];// 上边(temp) -> 右边matrix[i][last] = temp;}
}
- 外层循环控制处理的层数,从最外层(layer=0)开始,一直到最内层。
- 对于一个n×n的矩阵,总共有n/2层(如果n是奇数,最中心的元素不需要旋转)。
first表示当前层的起始位置,last表示当前层的结束位置。
// 对当前层的每个元素进行旋转
for (int i = first; i < last; i++) {// ...
}
- 内层循环处理当前层的每个元素。
- 对于每个位置(first,i),我们找出旋转后对应的其他三个位置,然后一次性完成旋转。
// 存储上边的元素
int temp = matrix[first][i];// 左边 -> 上边
matrix[first][i] = matrix[n - 1 - i][first];// 下边 -> 左边
matrix[n - 1 - i][first] = matrix[last][n - 1 - i];// 右边 -> 下边
matrix[last][n - 1 - i] = matrix[i][last];// 上边(temp) -> 右边
matrix[i][last] = temp;
- 这四行代码完成了四个位置的旋转。
- 首先,我们保存上边的元素到
temp。 - 然后,将左边的元素移动到上边,下边的元素移动到左边,右边的元素移动到下边。
- 最后,将保存在
temp中的原上边元素移动到右边。
通过这种方式,我们实现了矩阵的顺时针旋转90度,并且是在原矩阵上直接修改的。
4.4 复杂度分析
- 时间复杂度: O(n²),其中 n 是矩阵的边长。虽然我们使用了两层循环,但并没有访问矩阵中的所有元素,只访问了大约四分之一的元素。然而,在渐近意义上,这仍然是O(n²)。
- 空间复杂度: O(1),我们只使用了常数额外空间(一个临时变量)。
4.5 适用场景
四点旋转法更符合矩阵旋转的直接定义,不需要理解转置和翻转的组合。这种方法适用于需要直接模拟旋转过程的场景,例如:
- 在图像处理中,当需要理解或可视化旋转过程时
- 当问题要求追踪每个元素在旋转过程中的确切路径时
- 在教学中解释矩阵旋转的具体流程时
5. 详细步骤分析与示例跟踪
让我们通过具体的例子详细跟踪每种解法的执行过程,以深入理解算法的工作原理。
5.1 解法一:3×3矩阵示例
以示例1中的3×3矩阵为例:
1 2 3
4 5 6
7 8 9
第一步:转置矩阵
-
初始状态:
1 2 3 4 5 6 7 8 9 -
转置矩阵意味着交换对角线上方的元素,即交换(i,j)和(j,i):
- 交换(0,1)和(1,0):将2和4交换
1 4 3 2 5 6 7 8 9- 交换(0,2)和(2,0):将3和7交换
1 4 7 2 5 6 3 8 9- 交换(1,2)和(2,1):将6和8交换
1 4 7 2 5 8 3 6 9 -
转置完成后的矩阵:
1 4 7 2 5 8 3 6 9
第二步:左右翻转每一行
-
初始状态(转置后的矩阵):
1 4 7 2 5 8 3 6 9 -
对每一行进行左右翻转:
- 第一行:交换1和7
7 4 1 2 5 8 3 6 9- 第二行:交换2和8
7 4 1 8 5 2 3 6 9- 第三行:交换3和9
7 4 1 8 5 2 9 6 3 -
最终结果:
7 4 1 8 5 2 9 6 3
这就是顺时针旋转90度后的矩阵。
5.2 解法二:3×3矩阵示例
以同样的3×3矩阵为例:
1 2 3
4 5 6
7 8 9
使用四点旋转法:
-
初始状态:
1 2 3 4 5 6 7 8 9 -
分析层数:
- 3×3矩阵只有1层(最外层)
- first = 0, last = 2
-
对第0层的每个元素进行旋转(从first到last-1):
-
处理元素(0,0):
- 保存temp = matrix[0][0] = 1
- 左边到上边:matrix[0][0] = matrix[2][0] = 7
- 下边到左边:matrix[2][0] = matrix[2][2] = 9
- 右边到下边:matrix[2][2] = matrix[0][2] = 3
- 上边到右边:matrix[0][2] = temp = 1
7 2 1 4 5 6 9 8 3 -
处理元素(0,1):
- 保存temp = matrix[0][1] = 2
- 左边到上边:matrix[0][1] = matrix[1][0] = 4
- 下边到左边:matrix[1][0] = matrix[2][1] = 8
- 右边到下边:matrix[2][1] = matrix[1][2] = 6
- 上边到右边:matrix[1][2] = temp = 2
7 4 1 8 5 2 9 6 3
-
-
最终结果:
7 4 1 8 5 2 9 6 3
5.3 4×4矩阵示例
以示例2中的4×4矩阵为例:
5 1 9 112 4 8 10
13 3 6 7
15 14 12 16
使用解法一(转置+翻转):
-
转置矩阵后:
5 2 13 151 4 3 149 8 6 12 11 10 7 16 -
左右翻转每一行后:
15 13 2 5 14 3 4 1 12 6 8 9 16 7 10 11
使用解法二(四点旋转法):
对于4×4矩阵,我们需要处理2层:最外层和次外层。
-
处理最外层(layer=0):
- first = 0, last = 3
- 依次旋转(0,0), (0,1), (0,2)对应的四个点
- 旋转后变为:
15 13 2 5 14 4 8 1 12 3 6 9 16 10 7 11 -
处理次外层(layer=1):
- first = 1, last = 2
- 旋转(1,1)对应的四个点
- 旋转后变为:
15 13 2 5 14 3 4 1 12 6 8 9 16 7 10 11
5.4 特殊情况:奇数大小的矩阵
对于奇数大小的矩阵(例如5×5),中心点不需要旋转。
例如5×5矩阵:
1 2 3 4 56 7 8 9 10
11 12 13 14 15
16 17 18 19 20
21 22 23 24 25
- 解法一(转置+翻转)不受影响,照常操作即可。
- 解法二(四点旋转法)需要处理2层(最外层和次外层),中心点(2,2)不需要处理。
5.5 动态示意图
下面是旋转过程的动态示意图:
解法一:转置+翻转
原始矩阵: -> 转置后: -> 左右翻转后:
1 2 3 1 4 7 7 4 1
4 5 6 -> 2 5 8 -> 8 5 2
7 8 9 3 6 9 9 6 3
解法二:四点旋转
旋转(0,0)位置的四个点: 旋转(0,1)位置的四个点:
1 2 3 7 2 1
4 5 6 -> 4 5 6 ->
7 8 9 9 8 3最终结果:
7 4 1
8 5 2
9 6 3
6. 常见错误与优化
6.1 常见错误
-
转置矩阵时的索引错误:
在解法一中,转置矩阵时常见的错误是内层循环的起始点选择。// 错误写法:会导致重复交换 for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) { // 错误:应为j = iint temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;} }// 正确写法:避免重复交换 for (int i = 0; i < n; i++) {for (int j = i; j < n; j++) { // 从i开始,避免重复交换int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;} } -
左右翻转时的范围错误:
翻转每行时,只需要遍历到行的一半位置。// 错误写法:会导致重复交换,使结果不变 for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) { // 错误:应为j < n/2int temp = matrix[i][j];matrix[i][j] = matrix[i][n - 1 - j];matrix[i][n - 1 - j] = temp;} }// 正确写法:只遍历到一半 for (int i = 0; i < n; i++) {for (int j = 0; j < n / 2; j++) { // 只需交换一半int temp = matrix[i][j];matrix[i][j] = matrix[i][n - 1 - j];matrix[i][n - 1 - j] = temp;} } -
四点旋转法的下标计算错误:
在解法二中,容易在计算旋转后的四个点位置时出错。// 错误写法:下标计算错误 int temp = matrix[first][i]; matrix[first][i] = matrix[i][first]; // 错误:应为matrix[n-1-i][first] matrix[i][first] = matrix[last][i]; // 错误 matrix[last][i] = matrix[i][last]; // 错误 matrix[i][last] = temp;// 正确写法:正确计算旋转后的位置 int temp = matrix[first][i]; matrix[first][i] = matrix[n - 1 - i][first]; matrix[n - 1 - i][first] = matrix[last][n - 1 - i]; matrix[last][n - 1 - i] = matrix[i][last]; matrix[i][last] = temp; -
忽略特殊情况:
对于n=1的情况(单个元素的矩阵),旋转不会改变矩阵。需要检查这种特殊情况,避免不必要的操作。// 添加边界检查 if (matrix == null || matrix.length <= 1) {return; // 单个元素或空矩阵不需旋转 }
6.2 性能优化
-
减少交换次数:
在解法一中,转置矩阵时只需要交换对角线上方的元素,而不是整个矩阵。这已经在正确实现中体现。 -
原地操作优化:
两种解法都已经是原地操作,空间复杂度为O(1),已经是最优的。 -
循环优化:
在解法二中,可以考虑将四个点的旋转合并为一个表达式,减少临时变量的使用,但可能会降低代码的可读性。// 优化:直接四点交换 for (int layer = 0; layer < n / 2; layer++) {int first = layer;int last = n - 1 - layer;for (int i = first; i < last; i++) {int offset = i - first;int top = matrix[first][i];// 四点直接交换matrix[first][i] = matrix[last - offset][first];matrix[last - offset][first] = matrix[last][last - offset];matrix[last][last - offset] = matrix[i][last];matrix[i][last] = top;} } -
利用矩阵特性:
对于某些特殊矩阵(如对角矩阵、对称矩阵等),可以根据其特性简化旋转过程,但在通用解法中不适用。
7. 扩展题目与应用
7.1 相关矩阵变换问题
-
LeetCode 867. 转置矩阵:
给你一个二维整数数组 matrix,返回 matrix 的转置矩阵。矩阵的转置是指将矩阵的主对角线翻转,交换矩阵的行索引与列索引。这与我们解法一的第一步相似。 -
LeetCode 832. 翻转图像:
给你一个二维整数数组 A,每一个子数组中的元素代表一个像素点。将每一个子数组水平翻转,并将每个元素取反。这与解法一的第二步有相似之处。 -
LeetCode 73. 矩阵置零:
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。这也是一个要求原地修改矩阵的问题。
7.2 旋转相关的其他题目
-
LeetCode 189. 轮转数组:
给你一个数组,将数组中的元素向右轮转 k 个位置。这与矩阵旋转有相似的思想。 -
LeetCode 54. 螺旋矩阵:
按照顺时针螺旋顺序,返回矩阵中的所有元素。这与矩阵的旋转有一定的关联。 -
LeetCode 59. 螺旋矩阵 II:
生成一个按照顺时针螺旋填充的n×n矩阵。
8. 实际应用场景
矩阵旋转在实际应用中有许多用途,特别是在图像处理和计算机图形学领域:
-
图像处理:
- 数字图像可以表示为像素值矩阵,旋转图像就是旋转这个矩阵
- 在图像编辑软件(如Photoshop)中,图像旋转是基本功能
- 在OCR(光学字符识别)技术中,需要对倾斜的文档图像进行旋转校正
-
计算机图形学:
- 3D渲染中,物体的旋转可以通过旋转矩阵实现
- 游戏开发中,角色动画和场景变换常需要矩阵旋转
-
机器人技术:
- 机器人运动控制中,物体的旋转和移动需要矩阵变换
- 在路径规划算法中,需要考虑物体的旋转状态
-
科学可视化:
- 在数据可视化中,旋转视图可以从不同角度展示数据
- 医学影像(如CT、MRI)处理中,需要对三维图像进行重构和旋转
-
人工智能:
- 在计算机视觉中,图像旋转是数据增强的常用方法
- 在模式识别中,旋转不变性是重要的特性
-
地理信息系统:
- 在GIS中,地图的旋转和投影需要矩阵变换
- 卫星图像处理中需要考虑地球自转带来的旋转
-
游戏开发:
- 棋盘游戏(如俄罗斯方块、连连看等)中,图形元素的旋转
- 物理引擎中,碰撞检测和物体旋转的计算
这个旋转图像的算法提供了一种高效、原地的方法来执行90度旋转,适用于各种需要矩阵旋转的实际应用场景。
9. 完整的 Java 解决方案
以下是结合了各种优化和最佳实践的完整解决方案:
class Solution {/*** 旋转图像 - 转置+翻转法* 时间复杂度: O(n²)* 空间复杂度: O(1)*/public void rotate(int[][] matrix) {// 处理边界情况if (matrix == null || matrix.length <= 1) {return;}int n = matrix.length;// 沿对角线转置矩阵for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {// 交换matrix[i][j]和matrix[j][i]int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;}}// 左右翻转每一行for (int i = 0; i < n; i++) {for (int j = 0; j < n / 2; j++) {// 交换matrix[i][j]和matrix[i][n-1-j]int temp = matrix[i][j];matrix[i][j] = matrix[i][n - 1 - j];matrix[i][n - 1 - j] = temp;}}}/*** 备选方案 - 四点旋转法* 时间复杂度: O(n²)* 空间复杂度: O(1)*/public void rotateAlternative(int[][] matrix) {// 处理边界情况if (matrix == null || matrix.length <= 1) {return;}int n = matrix.length;// 从外层向内层处理,一共有 n/2 层for (int layer = 0; layer < n / 2; layer++) {int first = layer;int last = n - 1 - layer;// 对当前层的每个元素进行旋转for (int i = first; i < last; i++) {int offset = i - first;// 存储上边的元素int temp = matrix[first][i];// 左边 -> 上边matrix[first][i] = matrix[n - 1 - i][first];// 下边 -> 左边matrix[n - 1 - i][first] = matrix[last][n - 1 - i];// 右边 -> 下边matrix[last][n - 1 - i] = matrix[i][last];// 上边 -> 右边matrix[i][last] = temp;}}}
}
这个完整的解决方案提供了两种实现方法:
rotate方法实现了转置+翻转的解法,代码简洁明了rotateAlternative方法实现了四点旋转法,更直观地模拟了旋转过程
两种方法都处理了边界情况,并使用了最优的实现方式。在实际应用中,可以根据需要选择任意一种方法。
10. 总结与技巧
10.1 解题要点
-
理解矩阵旋转的几何意义:
- 顺时针旋转90度使第一行变成最后一列,第二行变成倒数第二列,依此类推
- 了解点(i,j)旋转后的新位置是(j,n-1-i)
-
寻找数学规律:
- 转置+翻转的组合等同于90度旋转
- 四个点之间存在循环旋转关系
-
原地操作技巧:
- 利用临时变量完成元素交换
- 避免重复操作,如在转置矩阵时只处理对角线上方的元素
-
分层处理思想:
- 在四点旋转法中,从外到内一层一层处理矩阵
- 对于每一层,按照相同的模式旋转四个对应点
-
边界条件处理:
- 注意空矩阵和单元素矩阵的特殊情况
- 对于奇数大小的矩阵,中心点不需要旋转
10.2 学习收获
通过学习旋转图像问题,你可以掌握:
- 矩阵操作的基本技巧
- 空间几何变换的数学关系
- 原地算法的设计思想
- 分解复杂问题为简单操作的能力
10.3 面试技巧
如果在面试中遇到此类问题:
- 先分析问题,理解旋转的定义和要求
- 从最直接的解法开始,如四点旋转法,这样易于展示思考过程
- 可以提出转置+翻转的优化方法,展示数学思维能力
- 讨论边界情况和可能的优化
- 提及该问题在实际应用中的意义,如图像处理
特别注意,这个问题容易出错的地方是索引计算,因此在面试中实现时要格外小心。
10.4 考察重点
这道题主要考察:
- 矩阵操作能力
- 空间想象力
- 原地算法设计
- 边界条件处理
- 代码实现的细节把控
11. 旋转矩阵的数学原理
为了更深入地理解矩阵旋转,我们可以从数学角度分析旋转变换的原理。
11.1 线性代数视角
在线性代数中,二维平面上的旋转可以通过旋转矩阵表示。顺时针旋转90度的旋转矩阵为:
R = [ 0 1][-1 0]
对于点(x,y),旋转后的新坐标(x’,y’)可以通过矩阵乘法计算:
[x'] [ 0 1] [x]
[y'] = [-1 0] [y]
展开得:
x' = y
y' = -x
将这个公式应用到矩阵索引上,假设点(i,j)在旋转后变为(i’,j’):
i' = j
j' = n-1-i
这正是解法一中的转置(i’=j, j’=i)和左右翻转(j’=n-1-j’)所实现的效果。
11.2 四点旋转的数学关系
在解法二中,我们旋转了四个位置的点。这四个位置形成了一个循环:
(i,j) -> (j,n-1-i) -> (n-1-i,n-1-j) -> (n-1-j,i) -> (i,j)
这种循环关系可以通过连续应用旋转变换得到:
- 点(i,j)旋转90度后变为(j,n-1-i)
- 再旋转90度变为(n-1-i,n-1-j)
- 再旋转90度变为(n-1-j,i)
- 再旋转90度回到原点(i,j)
这个循环恰好是360度的完整旋转,因此四个点形成了一个封闭的变换循环。
11.3 转置和翻转的组合等价性
我们可以证明转置和翻转的组合等价于旋转:
- 转置操作:(i,j) -> (j,i)
- 左右翻转操作:(j,i) -> (j,n-1-i)
- 组合结果:(i,j) -> (j,n-1-i)
这正是顺时针旋转90度的结果。
