算法题（153）：哈夫曼编码

1.前置知识讲解

1.树的带权路径长度：

从树的根到树的其中一个叶子结点的路径长度与该叶子结点权值的乘积为该叶子结点的带权路径长度。

一棵树的所有叶子结点的带权路径长度之和就是树的带权路径长度

eg：

对于权值为1的叶子结点来说：他的带权路径长度就是根节点到他的距离（2）X自己的权值(1),得到结果为2

对于整棵树来说：带权路径长度就是所有的叶子结点的带权路径长度之和
2.哈夫曼树：

在含有n个带权叶子结点的二叉树中，树的带权路径长度最小的二叉树就是哈夫曼树，也叫最优二叉树

3.哈夫曼算法：用来构建哈夫曼树的算法

第一步：初始化

我们将所有的带权叶子结点分别当成一颗颗树，那么所有叶子结点就组成了一片森林

第二步：树的合并

我们将权值最小的叶子结点从森林取出，当成一颗新树的左右子节点，然后合成一颗新树，这颗新树的根节点的值为左右子节点权值相加，然后我们把这颗新树的根节点当成森林中的一颗新树

第三步：重复第二步直到森林中只有一棵树为止

如此我们就得到了一颗哈夫曼树

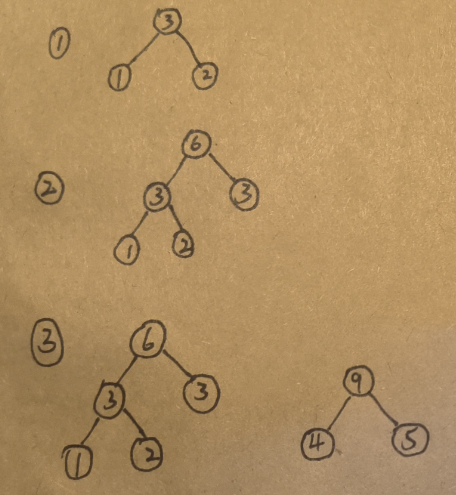
eg：假设我们的带权叶子结点有（1,2,3,4,5,6）

第一步：将最小的带权节点1,2合并为一颗树。合并后将新的树的根节点3放入森林

森林：3,3,4,5,6

第二步：将3,3合并为一棵树，将6放入森林

森林：4.5.6.6

第三步：将4,5合并为一棵树，将9放入森林

森林：6.6.9

第四步：将6.6合并为新树，将12放入森林

森林：9.12

第五步：将9.12合并为新树，将21放入森林

森林：21

此时只有一颗树了，哈夫曼树构建完成

整棵树的带权路径和求法：

直接在构建的同时将所有子节点的权值累加起来即可

eg：

其实带权路径也可以用另一种方式理解，那就是我们其实是将权值赋予给了路径，比如权值为2的叶子结点，他的单位路径值就从1赋值为了2。我们看左图，权值为1的带权路径就是1，权值为2的带权路径位2。

那么我们再看看右图：

按照传统求法我们得到树的带权路径和为9，用构建哈夫曼树时所有子节点累加也可以得到结果9

疑问：为什么可以这样计算树的带权路径和？
对于1,2的根节点3其实我们加上他的值的时候，本质上是加上1,2的 新一段路径长度的值

4.哈夫曼编码：一种用于压缩的编码方式

比如说我们有一个字符串“aabbccdd”，正常来说我们需要给每个字符8bit位置存储，但是经过编码后我们甚至可以只用2bit表示一个字符

编码流程：

1.统计字符的出现次数

2.将次数作为对应字符叶子结点权值构建哈夫曼树

3.构建完成后给所有相对于其根节点的左路径标为0，给右路径标为1，根据路径得出最终编码

eg：

2.算法题讲解

 

审题：

本题需要我们找到编码后字符串的最短长度

思路：
方法一：哈夫曼编码

字符串最短长度其实就是题目中说的哈夫曼编码长度乘字符出现次数，而哈夫曼编码长度等于字符路径长度，字符出现次数等于叶子结点权值。

所以题目其实就是要我们求经过哈夫曼树构建后的树带权路径和

解题：
 

#include<iostream>
#include<vector>
#include<queue>
using namespace std;
typedef long long ll;
int n;
priority_queue<ll, vector<ll>, greater<ll>> p;
int main()
{//数据录入cin >> n;for (int i = 1; i <= n; i++){ll a;cin >> a;p.push(a);}//哈夫曼编码ll answer = 0;while (p.size() != 1){ll a = p.top(); p.pop();ll b = p.top(); p.pop();answer += a + b;p.push(a + b);}cout << answer << endl;return 0;
}

1.我们需要快速获得最小的两个权值，所以我们使用小堆结构，而priority_queue默认是大堆，所以我们要传greater仿函数来控制排序逻辑为小堆

2.我们计算树的带权路径和的方法是累加构造哈夫曼树过程中的所有子节点的权值

哈夫曼编码