计算机图形学Games101笔记--光线追踪。RTX ON!!!(＜--删除线）

前排提醒，如果你没有听过Games101建议取听一下：Games 101。
本博文仅作为复习笔记或者快速浏览。不适用于从零开始了解光线追踪

第三部分 光线追踪

为什么需要光线追踪？

1. 软阴影
2. Glossy reflection & indirct illumination 光线在场景中反射很多次才传播到人的眼睛
3. 光栅化是一个很快的近似的渲染方法，一般用于实时应用。

光线追踪的三个ideas

1. 光是绝对的直线
2. 光线相交不会冲突
3. 光线从光源传到眼睛（第三个idea利用了光的可逆性，）
   ![外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传](https://img-home.csdnimg.cn/images/20230724024159.png?origin_url=assets%2Fimage-20250516135551273.png&pos_id=img-tfNaYNQj025051613555127

光线追踪认为光线完美的反射

光线投射

只考虑光线的一次折射。眼睛传过每个像素，找到与第一个物体的交点。然后从改点与光源进行连线。得到眼睛到光源的路径，我们认为光沿这个路径传播。找到交点的法线后执行shading计算。

阴影

核心思想：点不在阴影中当且仅当能被光源看到也能被摄像机看到。

shadow mapping只能处理点光源，有明显的边界。

操作：

1. 记录光源位置虚拟相机下的深度图

2. 把眼睛位置真实相机能看到的点投影回光源位置虚拟相机的平面上，并且获得一个深度。如果该深度和光源位置虚拟相机记录的深度相同。则表示该点是可见的。否则该点不可见。

   

个人理解：

1. 在光源位置记录一个深度图
2. 从眼睛位置看，把能看到的所有点都投影回光源处，投影的时候会有一个深度，判断这个深度和记录的深度图上的深度是否一致，如果不一致，则该点在阴影里。

限制：

1. 只能做硬阴影（只支持点光源）

   现实世界中光源并非是点光源，阴影分为硬阴影和软阴影。

   

2. 是否相等判断很困难（计算机存储的浮点数精度问题）。引入一个bias，并且用大于替代等于。

3. shadow mapping分辨率大小问题。同纹理分辨率的问题。

Whitted-Style Ray Tracing

主要思想

光线经过物体后会发生反射和折射，我们从眼睛到每个像素画一条射线，如果射线与物体相交则会发生反色和折射，反射和折射的光线基于传播和打到其他物体上（递归）。之后我们判断光源是否可以直接照射这些交点，如果可以则会形成一个传播路径。

光线打到透明物体，发生镜面反射和折射，光线达到漫反射物体则不会进一步传播（停止）

光线和简单物体【隐式】的交点

**光线定义：**我们把光源定义为点光源（O)，光线的方向为d。光线定义为$r(t)=o+td$

**球的定义：**我们用隐式表示的方法定义球面。

**【隐式表面】光线和球的交点：**光线与球面的交点应该满足光线和球的隐式表达式。即光线t时刻的点带入球的表达式解出t。

**【隐式表面】【推广】光线和一般物体的交点：**将光线t时刻的点带入一般物体的隐式表达式，求解t.

---

光线与三角形【显式】的交点

我们对每个三角形判断光线是否与该三角形有交点（一个一个三角形判断显然可以，但是很慢，后面介绍加速方法）。下面我们介绍如何计算光线和三角形的交点。

1. 首先计算光线和三角形所在平面的交点。我们用法线和平面上的p点来表示平面。任意一点和p点的连线应该与法线垂直。因此，光线与平面的交点和p点的连线也应该和平面法线垂直（平面法线就是三角形的法线）。因此我们可以通过解下面的方程来得到光线与三角形所在平面的交点
   

2. 判断光线与三角形所在平面的交点是否在三角形内。通过向量叉乘的方式。

==Moller Trumbore（MT）算法，基于三角形重心坐标计算光线是否与三角形相交（faster）==如果光线和三角形有交点，那么交点一定可以用三角形的重心坐标给出。因此我们可以写出下面的线性方程，该方程左侧是用光线的定义得到的交点，右侧是三角形的重心坐标得到的交点。该方程有三个未知量，t,b1,b2。有三个等式（三个坐标，对每个坐标都满足，因此有三个等式）。接这个线性方程判断t是否大于零，b1,b2是否大于零并且小于1。如果满足则光线与三角形有交点，交点就是o+td。

---

快速计算光线与场景的交点

光线与包围盒的交点

**包围盒：**三个对面的交集（长方体包围盒）。光线进入所有对面的最晚时间光线进入了盒子，光线离开任何一个对面，则光线离开了这个盒子。如果光线进入时间小于离开时间则光线传过盒子。

包围盒一般用轴对齐的包围盒（Axis-Aligned Bounding Box,AABB），因为我们可以很容易计算光线与某个与坐标轴垂直平面的交点。

**光线与垂直于x/y/z轴的平面的交点：**t==（交点的x轴分量（就是px)-光源x轴分量）/单位光线在x轴上的投影长度

1. 先计算物体与包围盒是否有交点。计算光线进入包围盒的时间和离开包围盒的时间。

   如果离开时间小于0，则光线和盒子不相交（盒子在光线背面）

   如果离开时间大于0，进入时间小于0，则光线起点就在盒子里，一定与盒子相交。

   如果离开时间大于0，进入时间大于0，且进入时间小于离开时间，则光线一定穿过包围盒

   如果离开时间大于0，进入时间大于0，且进入时间大于离开时间【见下图的解释】，则光线在包围盒旁边。

==总结：当且仅当进入时间小于离开时间，离开时间非负，光线与盒子才有有交点。==

使用包围盒加速-空间划分

直接划分：

我们把整个场景划分为等大的包围盒，然后标记包围盒是否包含物体。对于任意一个光线，我们沿着光线传播方向计算光线是否穿过包围盒（如果光线穿过包围盒，并且向右方传播，那么光线仅可能穿过该包围盒上，右，右上三个包围盒）。

有一些启发式的算法表明，在3D空间下包围盒应该划分成27*obj_num个。

这种简单划分包围盒的方法不太适用（然而实际中也会使用该方法）于某些空间物体密集，某些空间物体稀疏的情况。

空间划分：

光线追踪之前先做好空间划分。

oct-tree和维度相关，每个维度都切一下。【和维度有关】

KdTree只在某个轴上划分，划分的轴按照xyz的循环顺序。

BSP-Tree，每一次选一个方向和KdTree的区别每次选的方向不是横平竖直的。【维度高的时候会越来越不好计算】

KdTree：

非叶结点存储：

1. 划分轴，x，y或z
2. 分割位置，分割平面沿着分割周的坐标
3. 左右孩子的结点
4. 有没有物体存在于该内部结点

叶节点存储：

1. 物体的列表

使用KdTree进行光线追踪

中序遍历，从根节点开始，如果光线穿过某个结点，且该节点不是叶节点，则继续判断光线是否穿过孩子结点。如果光线穿过某个节点且该结点是叶节点，则判断光线是否穿过叶节点内的物体。

三角形和包围盒是否有交集很难实现（有具体的算法，但是需要考虑各种特殊情况）。一个物体可能存在多个包围盒里）

使用包围盒加速-物体划分(BVH)

把物体分为左右两部分，并计算包围盒（递归）。然后在任意一个包围盒中继续划分。两个包围盒可能存在重叠，但是包围盒中的物体不会出现在其他包围盒中。

1. 物体划分左右两部分的时候可以按照xyz轴的顺序划分。

2. heuristic #1 还可以总是选择最长的轴划分（切分包围盒最长的轴）

3. heuristic #2 再中间物体的位置划分结点。

4. 1 & 2 确定轴，找到三角形的重心，找到三角形重心的中位数（有一个快速的算法找到无序序列中的中位数），划分包围盒。

5. termination criteria。每个结点包含至少5个结点。

使用划分后的包围盒求光线和三角形交点

辐射量学 Basic radiometry

Motivation

在Blinn-Phong模型中，光线强度是I，I可能是10，我们把它简化为一个数，那么这个数是什么？

Whitted style的光线追踪并不是Correct结果！因为我们假设全反射，假设折射系数等等。

而辐射度量学就是一个精准的描述光的一系列物理量的方法，我们可以把光精确定义出来；可以把物体表面如何与光进行相互作用精确的描述出来；可以把光源、材质和光线的传播方法精确的做出来。

Radiant Energy 辐射能 and Flux 辐射通量（power）

辐射能Radiant Energy：辐射能是电磁辐射的能量。它的单位是焦耳，用符号表示

辐射通量（功率）power：是单位时间内发射、反射、发射或接收的能量。

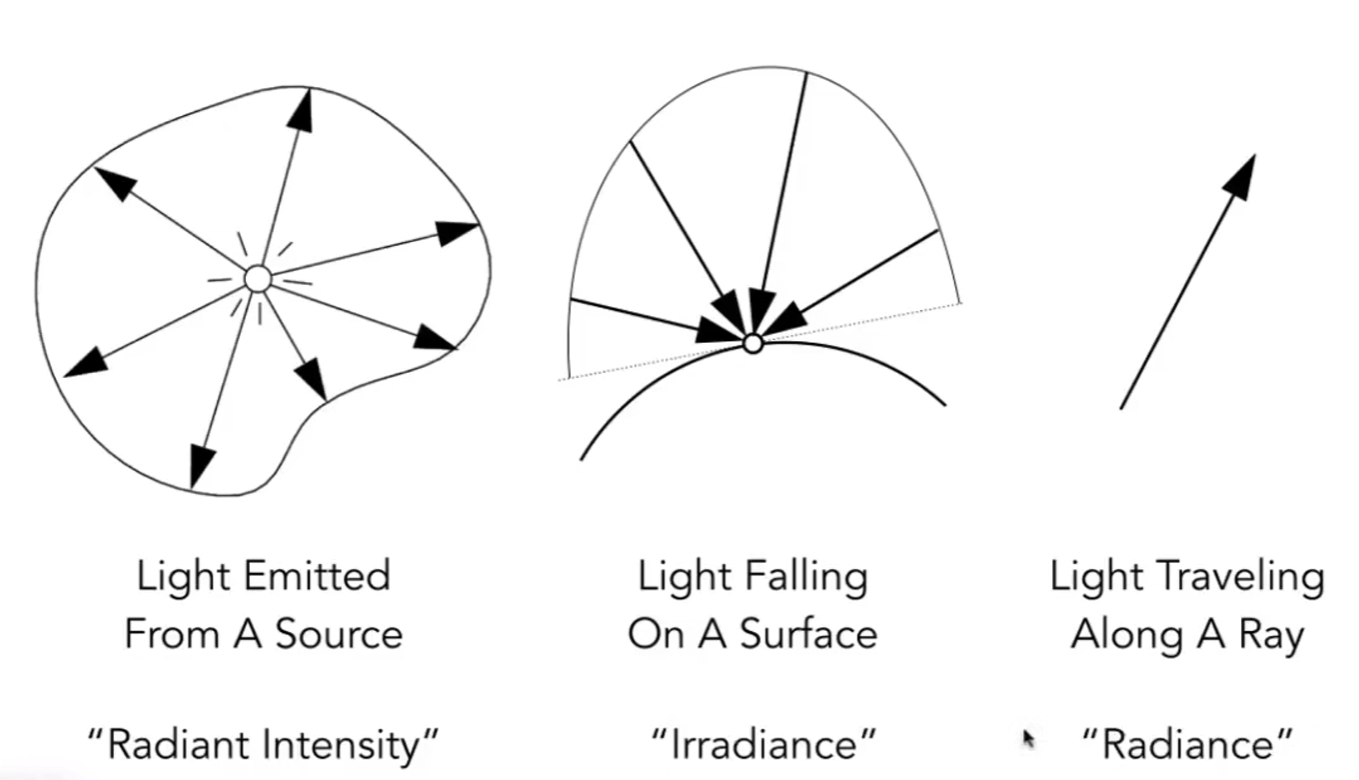
Radiant Intensity，Irradiance，Radiance的关系图

辐射强度：描述单位立体角内辐射源的辐射功率（可以看作辐射通量在单位立体角内的分量）

radiance：光线沿着某个方向传播

irradiance：所有落在物体某个点上的光线

辐射强度 Radiant Intensity (I)

立体角，我们从平面触发，圆上的角可以用对应的弧长和半径的比值决定。扩展到三维空间，球上的一个立体角可以用球面上的面积和半径平方的比值描述。

单位立体角：对于从球心触发的任意一个射线，我们可以得到改射线偏离z轴的角度θ和偏离x轴的角度o。单位立体角对应的面积可以看作是一个长方形，长宽分别为平面上θ和o对应的单位弧长。对于θ角对应的弧长，我们可以直接用rdθ表示（平面上的弧长计算公式），而对于o对应的弧长,rdo表示的o角对应的最大弧长，因此还需要乘以sinθ。综上，单位立体角计算如下：

对单位立体角求积分得到的是球的面积。

辐射通量等于辐射强度对于球表面的积分。对于均匀辐射的点光源。辐射强度等于辐射通量/4Π

Irradiance E(x)

单位面积内的power（辐射通量）。注意这里的面积需要和光线垂直。

理解为什么远离光源的物体接受的光少：

Radiance（luminance）

每单位立体角，单位投影面积的power

Irradiance和radiance之间的关系（性质）

BRDF反射方程

Bidirectional Reflectance Distribution Function(BRDF)，双向反射分布函数

我们这么理解反射，光线沿着i角打到物体上，被物体吸收后，物体向r方向发射光线。BRDF则定义了i角度的光有多少被物体吸收然会发射到r方向。

反射方程：从下面方程我们可以看出，反射radiance依赖于入射radiance。这个入射radiance又会依赖其他反射radiance（光在场景下多次反射）

如何求解渲染方程？

我们可以把渲染方程写成如下的形式，其中I代求。

进一步，我们还可以把他写成简单的矩阵等式的形式（这一点是可以做的到，实际推到过程很复杂）

这样我们就可以求出L（极数）

全局光照：直接光照+简介光照

渲染方程（Rendering Equation）

我们在反射方程基础上增加一个自发光项，得到最终的渲染方程。

路径追踪

蒙特卡洛积分

我们在积分域上随机采样一个点，然后用这个点的f值除以概率密度值。

**直观理解：**如果我们均匀采样，则p(Xi)是b-a，Fn就是很多个以b-a为长，f(x)为高的矩形面积的平均值。

Problem of Whitted-Style Ray Tracing

• 总是执行镜面反射和折射，不适用于右图场景

  

• 遇到漫反射停止

  

利用蒙克拉洛积分解半球积分

从零开始-直接光照

我们假设光线从渲染点触发往外发射（和Bing-Phong模型假设一致）。我们对半球面均匀采样。$p(w_i)=1/2\pi$

伪代码如下：我们随机采样N个立体角，然后对于每个立体角，立体角判断是否到达光源，如果到达光源，则计算Radiance。

考虑全局光照

在直接光照基础上增加递归调用，如果到达光源直接计算，如果到达的是物体，则递归调用求该物体的Radiance

加速计算

上述算法存在计算爆炸的问题，假如一次采样100个立体角，则如果仅考虑两次简介光照（3次弹射，两次递归调用），则最后的光线变为了1000000个。

解决办法就是只采样一次！，很简单但是有效。我们把N次采样放在像素中，对于一条光线我们只采样一次。

!

增加递归调用的退出条件

到底应该考虑几次间接光照？在实际物理世界，光线会反射无数次，直到能量消耗完。

在渲染中，我们引入了俄罗斯赌盘（RR)来设置递归退出。

1. 我们以P的概率射出一条光线，如果P小于阈值，则渲染
2. 返回/P后的渲染结果$L_o/P$
3. 如果P大于阈值，则返回0

上述的步骤2，保证了期望是L0（保证了正确性）。增加RR后的算法如下：

从光源采样

对于每个像素，如果我们的采样次数太低，则会出现严重的噪声，如果采样次数太高，性能要求很高。此外如果光源面积很大，采样很少次数就可以，如果光源很小，需要采样很多次才可能碰到光源。

如果进行高效的采样？一种方法就是从光源采样。下面给出场景描述。

为了从光源采样计算蒙特卡洛定积分，我们还需要建立单位立体角和光源面积之间的联系。我们把光源正对p点，然后把光源面积投影回到单位立体角上。 （下图的球是单位球）

在光源面积上做积分的渲染方程

在渲染过程中，我们把采样分为两部分，从光源采样，和从立体角采样。从光源采样不需要RR，从立体角采样需要RR

算法如下：（个人观点，如果RR判定成功，需要一直采样到光线打到非光源处。在图形学中这些细枝末节的东西对实际效果基本没有影响，如果我们RR判定成功且碰到光源直接返回0，只需要略微提高P的阈值即可）

略微修改下采样光线的算法，考虑物体和光源之间是否有障碍物

限制

• 路径追踪点光源不好做，可以用面积非常小的面光源

⭐【扩展】

1. 非均匀采样半球（sampling研究方向）
2. 概率密度函数的选择（importance sampling）
3. 随机的质量对结果有影响？是的，更好的随机质量（分布均匀的随机）可以得到较好的结果。
4. 结合采样半球和采样光源（multiple imp. sampling）
5. 像素的radiance是所有通过它的radiance的平均？我们可以加权，比如像素中心点的radiance权重高（pixel reconstruction filter）
6. radiance是否就是像素的颜色？不是，还需要考虑gamma 修正，曲线，色彩空间。