【计量地理学】实验五 试验变异函数计算
一、实验目的
- 探索三种土壤属性的统计特征:通过对三种土壤属性进行描述性统计、异常值分析和正态分布统计,深入了解数据的分布特征、集中程度、偏度和丰度等信息;
- 研究三种土壤属性的空间分布特征:通过绘制三种土壤属性的空间分布图,了解其在空间上的分布趋势,为进一步研究土壤属性与地理位置之间的关系提供参考;
- 计算和分析试验变异函数值:通过计算各滞后距下的试验变异函数值,研究三种土壤属性的空间变异特征;
- 提高数据分析与可视化能力:通过本次实验的过程,提高了对数据的分析和可视化能力,包括书统计分析、绘制图表以及分析结果的解释。
二、实验内容
- 异常值分析
- 描述性统计
- 正态分布统计
- 空间分布统计
- 变异函数散点图
三、实验过程
(一)对三种土壤属性做基本统计分析,并描述其统计特征
1.异常值分析
在对三种土壤属性数据进行基本统计分析前,我们首先通过计算四分位间距,以此来确定异常值的上下限来检测数据中的异常值,在MATLAB中编写代码如下所示(pH),得到结果为:pH数据中无异常值,而有机质与全氮数据中则分别有一定量的异常值:

有机质结果:

全氮结果:
2.描述性统计
虽然我们在上述步骤中我们得到了有机质与全氮数据中的部分异常值,但出于对实验数据完整的考虑等原因,我们在后续实验过程中没有剔除这些异常值,首先我们进行描述性统计,具体包括:最值、均值、方差、标准差、变异系数、偏度、丰度,并绘制了频率直方图、箱线图与误差棒图,在MATLAB中编写代码如下所示:
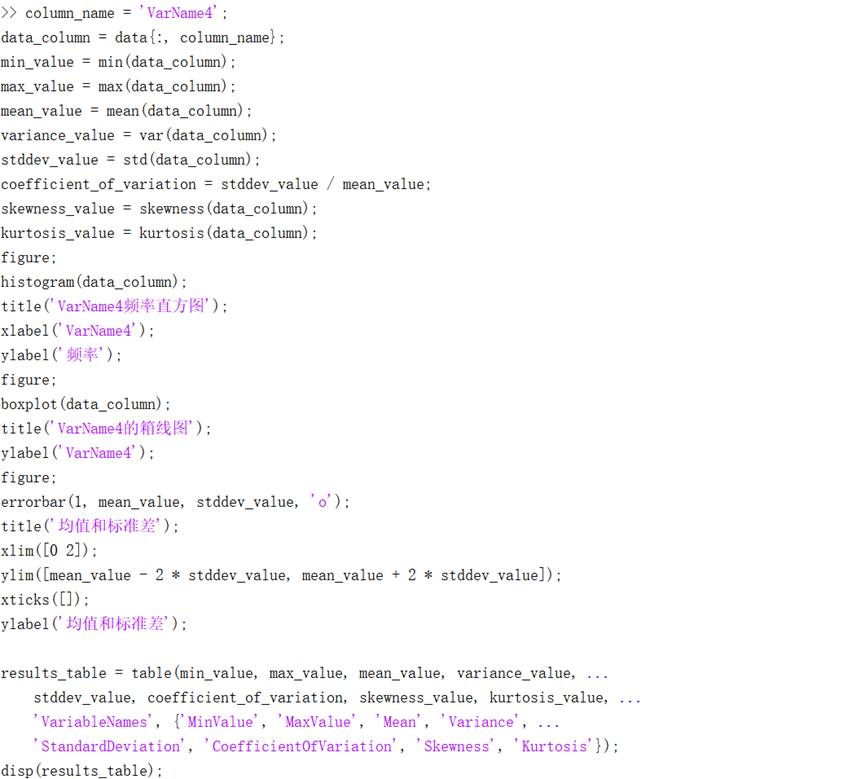
得到结果如下所示:
| 最小值 | 最大值 | 均值 | 方差 | 标准差 | 变异系数 | 偏度 | 丰度 | |
| pH | 5.1 | 8.1 | 6.616 | 0.4362 | 0.66045 | 0.099827 | 0.76257 | 2.8517 |
| 有机质 | 4.89 | 40.54 | 23.179 | 28.651 | 5.3526 | 0.23093 | -0.6475 | 3.1515 |
| 全氮 | 0.13 | 2.35 | 1.4466 | 0.0997 | 0.31582 | 0.21832 | -0.462 | 3.4301 |
| pH | 有机质 | 全氮 | |
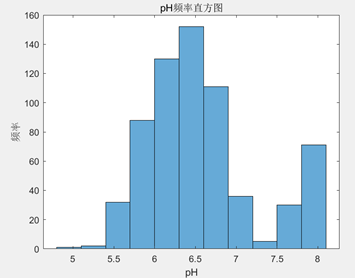
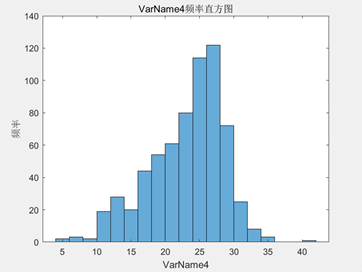
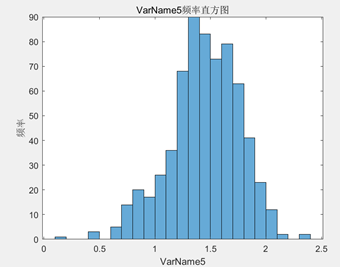
| 频 率 直 方 图 |
|
|
|
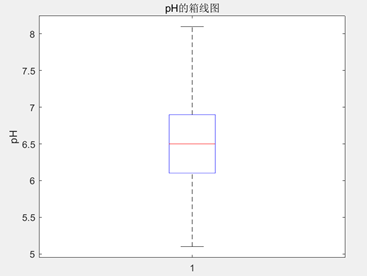
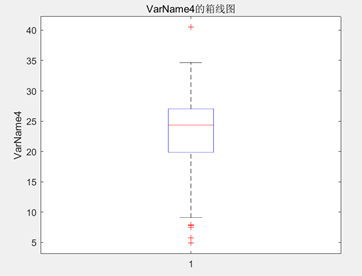
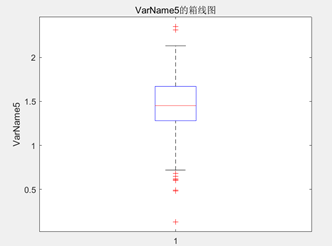
| 箱 线 图 |
|
|
|
| 误 差 棒 图 |
|
|
|
分析:
- pH:pH 值的范围为(5.1,8.1),pH值的范围较为广泛,但均值为 6.616,表明大部分数据集中在接近中性pH的范围,而方差和标准差较小,分别为 0.4362 和 0.66045,说明pH值相对集中,波动较小,变异系数为 0.099827,表示数据的变异程度相对较小同样佐证了这一点,偏度为0.76257,意味着pH值稍微向右偏,丰度为 2.8517,则表明数据峰值较高;
- 有机质:有机质含量的范围为(4.89,40.54),有机质的范围较为广泛,但均值为23.179,表明大部分数据集中在较高有机质含量的范围,而方差和标准差较高,分别为28.651和5.3526,说明有机质含量波动较大,变异系数为0.23093,表示数据的变异程度较小同样佐证了这一点,偏度为-0.6475,意味着有机质含量稍微向左偏,丰度为3.1515,则表明数据峰值较高;
- 全氮:全氮含量的范围为(0.13,2.35),全氮的范围较为广泛,但均值为1.4466,表明大部分数据集中在较高全氮含量的范围,而方差和标准差较小,分别为0.0997和0.31582,说明全氮含量波动较小,变异系数为0.21832,表示数据的变异程度相对较小同样佐证了这一点,偏度为-0.462,意味着全氮含量稍微偏向左偏,丰度为3.4301,则表明数据峰值较高。
3.正态分布统计
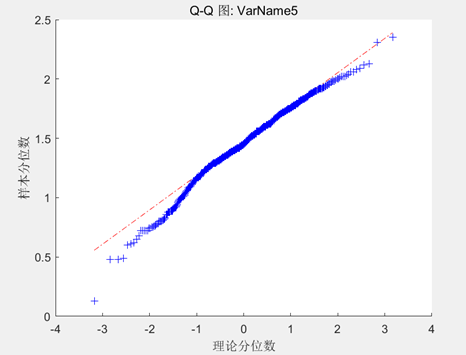
接下来我们对数据进行正态分布统计,通过观察数据与正态分布的偏离程度,来评估数据的正态性,以此作为数据分析和建模的基础,利用GIS空间分析课程的知识,我们选择在MATLAB中绘制Q-Q图,直观地展示数据与正态分布之间的匹配程度,以帮助我们更好地识别数据中的异常值和偏离点,代码如下所示:

得到结果如下表格所示:
| Q-Q图 | 分析 | |
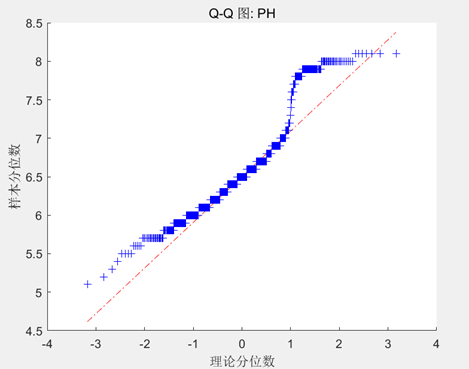
| pH |
| 如果样本数据与理论分布相符,数据点将沿着对角线分布,但如果数据点主要位于对角线的一侧或另一侧,则说明数据分布有偏态现象,由此我们可以判断出pH数据具有较强的正偏,不太符合正态分布。 |
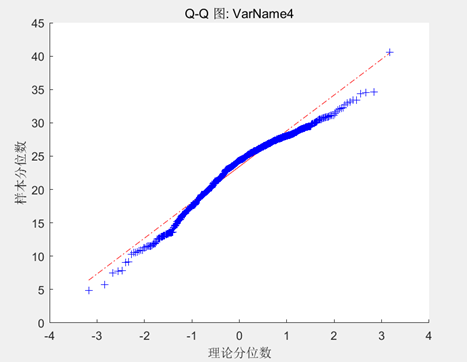
| 有机质 |
| 与pH值的数据相比,有机质的数据大部分都靠近对角线,说明数据基本符合正态分布,但两端远离对角线,则说明数据中存在一定的异常值。 |
| 全氮 |
| 与上述的有机质数据与pH值数据相比,全氮数据最为接近对角线,由此具有最强的正态分布性,但在数据下端依然存在一定的偏离(即异常值)。 |
4.空间分布统计
利用MATLAB软件我们绘制得到三种土壤属性的空间分布如下所示:
| 空间分布图 | 分析 | |
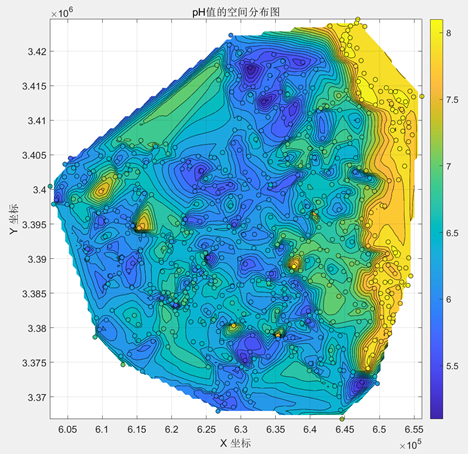
| pH |
| pH值的分布主要呈东北高,西南低的趋势,即研究区域内的东部具有较强的碱性,而研究区域内的西部具有较强的酸性。 |
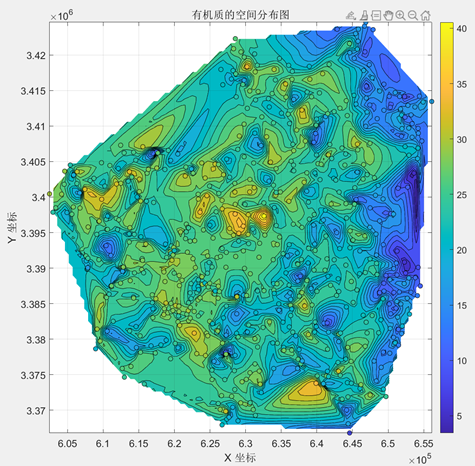
| 有机质 |
| 与pH值的数据相比,有机质的数据则与其呈反比关系,东部有机质含量较低,而西部有机质含量较高。 |
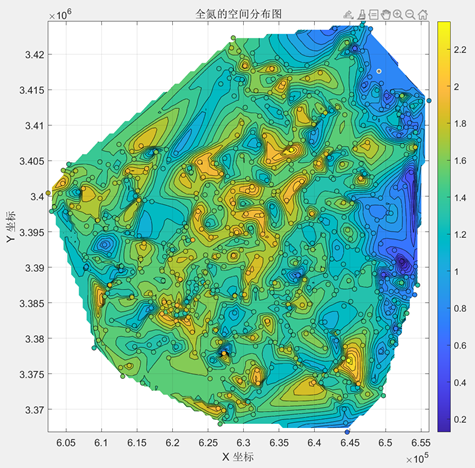
| 全氮 |
| 与上述的有机质数据与pH值数据相比,全氮数据的分布与有机质的分布相近,即东部全氮含量较低,而西部全氮含量较高。 |
(二)计算各滞后距下的试验变异函数值,并绘制试验变异函数散点图
在对三种土壤属性进行了基本的统计分析后,我们开始尝试计算各滞后距下的试验变异函数值,编写代码如下所示,该代码将计算和输出给定数据点的变异函数值,并将其保存在特定的.txt文件中,其核心思路为:通过遍历数据点列表,在指定的滞后距离范围内寻找符合条件的数据点对,计算其差异平方和累积半方差,即可得到各滞后距下的试验变异函数值:
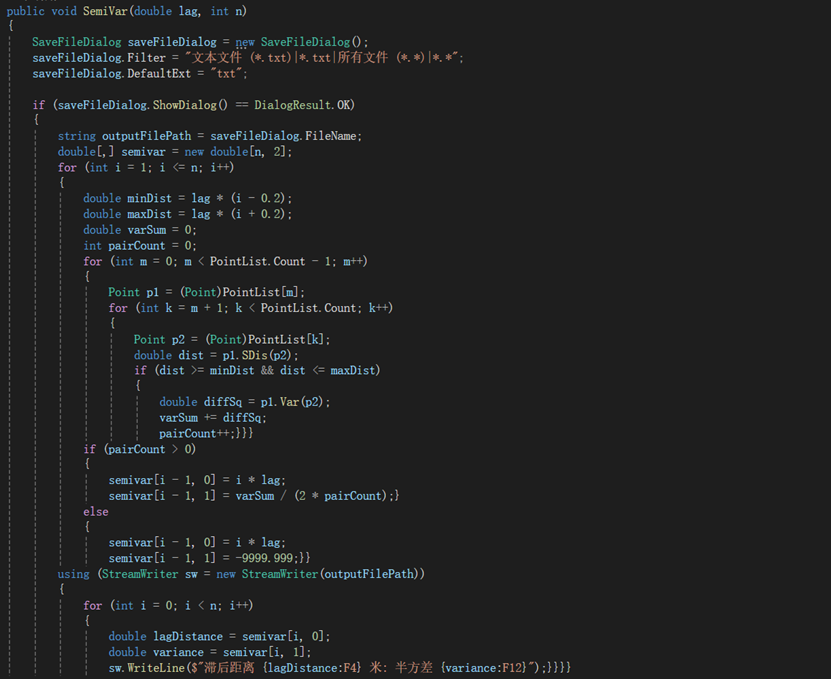
得到结果汇总如下所示:
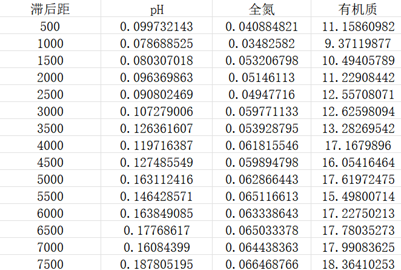
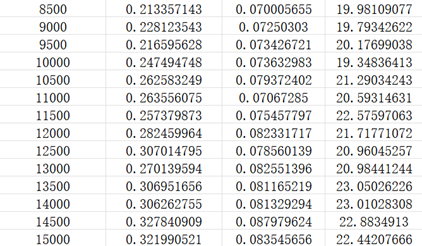
结果分析:
为深入研究三种土壤属性试验变异函数值的特征与机理,我们利用Excel软件与MATLAB中的绘图工具,尝试绘制试验变异函数散点图并拟合趋势线,得到结果如下所示:
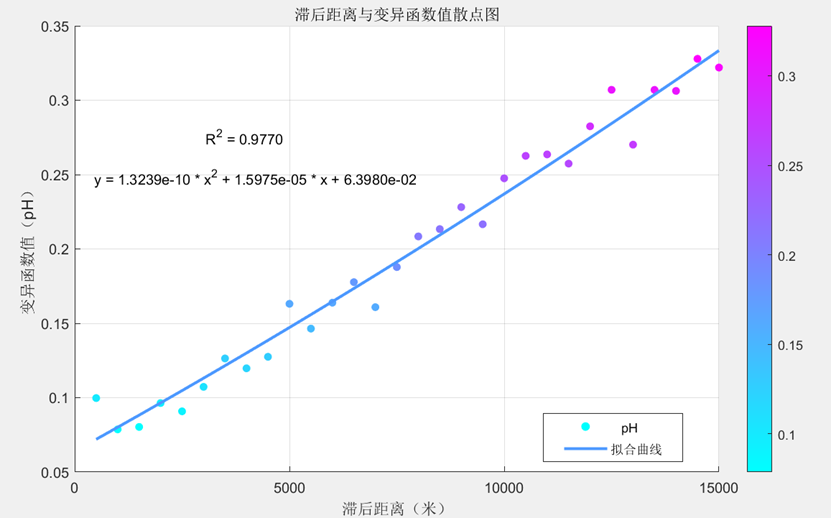
pH:
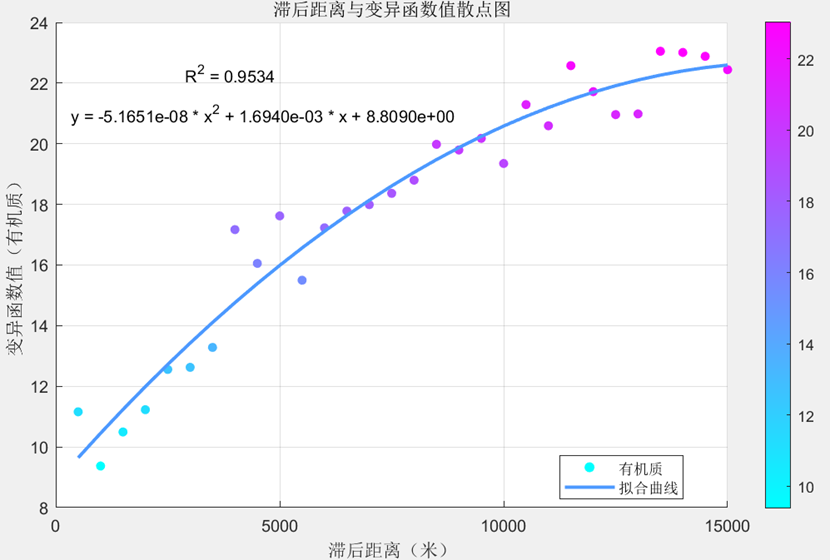
有机质:
全氮:
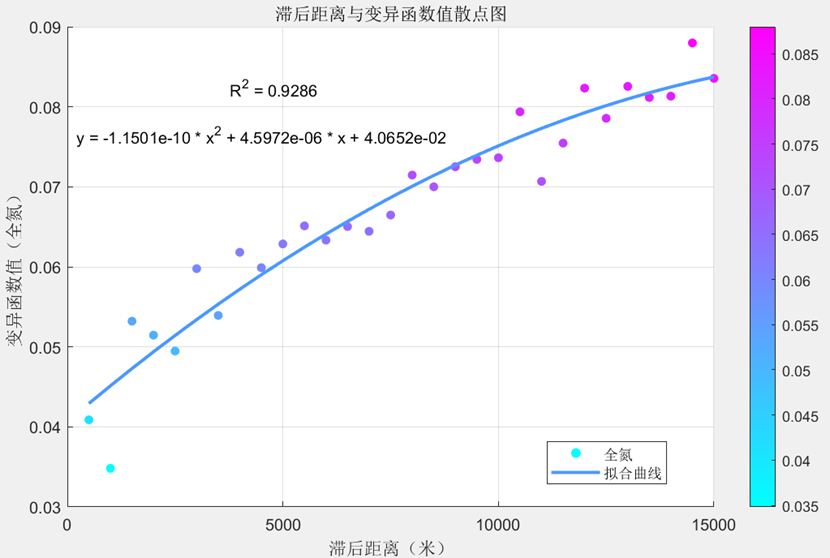
在对上述的三个变异函数值进行趋势线拟合时我们发现,绘制线性趋势线与多项式趋势线的差别并不大(尤其是pH值得变异函数值),但依然是二次的多项式R方要高于线性,三者的R方均高达0.9以上,因此我们可以认为拟合效果较好,且随着滞后距离增加,变异函数值不断增高,其起伏变化符合我们变异函数的基本定义,即随距离的增大而增大。
其中有机质与全氮得变异函数值已初步表现出了随着滞后距离增加趋于平稳的趋势,但由于滞后距离最值的限制,我们未能充分观察到拟合曲线的基台值、块金值与变程等详细的变异函数结构特征,有待后续的学习与补充。
四、实验心得
本次实验内容中首先回顾运用到了第一次实验课内容中的数据基本统计方法,并且系统分步的从异常值分析、描述性统计、正态分布统计与空间分布统计等四个方面进行开展,巩固了以往的学习内容。除此之外的一个重要内容为变异函数的计算与结构分析,本次实验中的代码编写并不困难,我认为收获最大之处在于对数据可视化处理的熟练程度提高与美化能力的提升,但遗憾未能绘制计算得到基台值等变异函数的显著特征,有待后续的实验学习。