数据结构初阶:二叉树(三)
概述:本篇博客主要介绍堆的应用等问题

1.堆的应用
1.1 堆排序
版本一:基于已有数组建堆,取堆顶元素完成排序版本
// 1、需要堆的数据结构
// 2、空间复杂度 O(N)
void HeapSort(int* a, int n)
{HP hp;for(int i = 0; i < n; i++){HPPush(&hp,a[i]);}int i = 0;while (!HPEmpty(&hp)){a[i++] = HPTop(&hp);HPPop(&hp);}HPDestroy(&hp);
}
https://blog.csdn.net/2401_87194328/article/details/147310043?spm=1001.2014.3001.5501
该链接是已有数组建的堆结构。
该版本有一个前提,必须提供现成的数据结构堆。
版本二:数组建堆,首尾交换,交换后的堆尾数据从堆中删掉,将堆顶数据向下调整选出次大的数据。
// 升序,建⼤堆
// 降序,建⼩堆
// O(N*logN)
void HeapSort(int* a, int n)
{// a数组直接建堆 O(N)for (int i = (n-1-1)/2; i >= 0; --i){AdjustDown(a, n, i);}// O(N*logN)int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}
1.2 堆排序时间复杂度计算
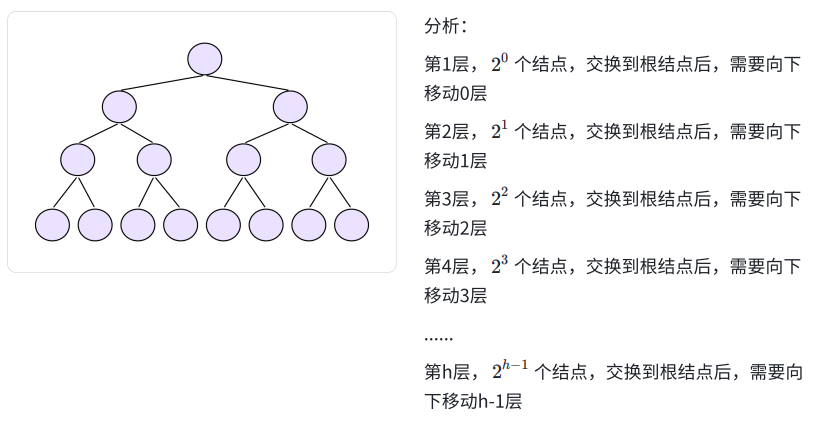
1.2.1 向下调整法:

1.2.2 向上调整法
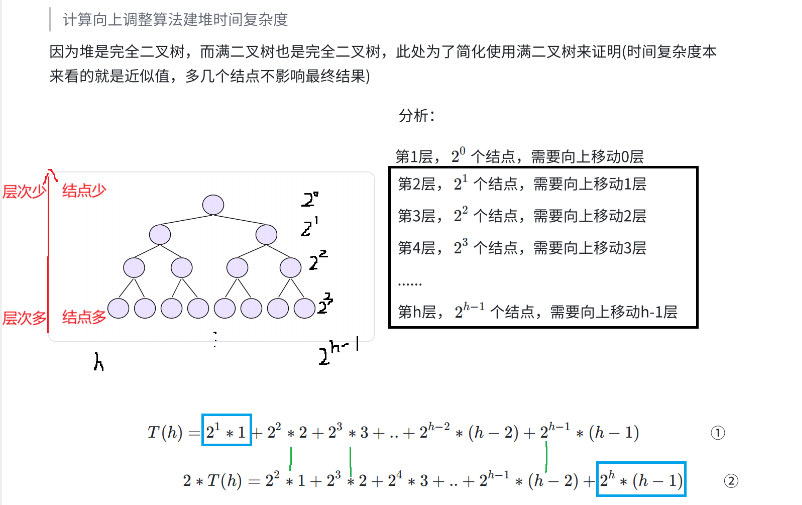
2式 - 1式 错位相减法可得:
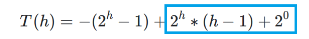
由二叉树的性质:
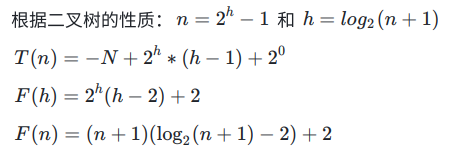
由此可得 :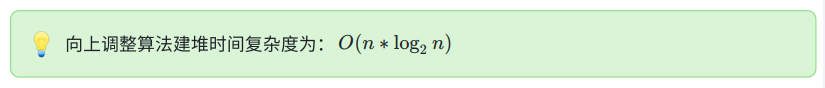
1.3 TOP-K 问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名,世界500强,富豪榜,游戏中前100的活跃玩家等等。
对于TOP-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全都加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1)用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆 前k个最小的元素,则建大堆

2)用剩余N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素
//TOPK
void CreateNDate()
{// 造数据int n = 100000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = (rand() + i) % 1000000;fprintf(fin, "%d\n", x);}fclose(fin);
}void Topk()
{int k = 0;printf("请输入K:");scanf("%d", &k);const char* file = "data.txt";FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen error");exit(1);}//找最大的前K个数据,建小堆int* minHeap = (int*)malloc(sizeof(int) * k);if (minHeap == NULL){perror("malloc fail!");exit(2);}for (int i = 0; i < k; i++){fscanf(fout, "%d", &minHeap[i]);}//建堆--向下调整建堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(minHeap, i, k);}//遍历剩下的n-k个数,跟堆顶进行比较,谁大谁入堆//调整堆int x = 0;while (fscanf(fout,"%d",&x) != EOF){if (x > minHeap[0]){minHeap[0] = x;AdjustDown(minHeap, 0, k);}}for (int i = 0; i < k; i++){printf("%d ", minHeap[i]);}fclose(fout);
}int main()
{//CreateNDate();Topk();return 0;
}
时间复杂度:
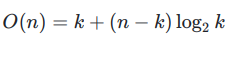
2.小结
以上便是本篇博客的所有内容,堆的使用当然更加广泛,TOP-K问题只是其中更为典型的的一种,博主只是展现堆的应用的冰山一角。如果本篇博客给大家带来知识,还请大家点点赞,支持支持。

