【漫话机器学习系列】252.零损失(0-1 Loss)
零一损失函数(0-1 Loss)详解及应用
在机器学习和统计建模中,损失函数用于衡量模型预测值与真实值之间的差距。今天,我们详细介绍一种最简单、直观但又很重要的损失函数——零一损失函数(0-1 Loss)。
本文将结合公式推导、图示解释,并给出实际应用场景,帮助大家系统掌握 0-1 损失的概念与意义。
1. 什么是零一损失函数?
零一损失函数,顾名思义,其取值只有两种:
-
当模型预测正确时,损失为 0;
-
当模型预测错误时,损失为 1。
直观上,它就是对预测结果的对错打分。
公式定义如下:
其中:
-
:样本 i 的真实类别。
-
:样本 i 的预测类别。
-
:指示函数,如果括号内条件成立,返回 1,否则返回 0。
简单来说:
-
如果
,即预测正确,
。
-
如果
,即预测错误,
。
2. 图解理解
来看一张示意图(来源:Chris Albon,中文标注版):
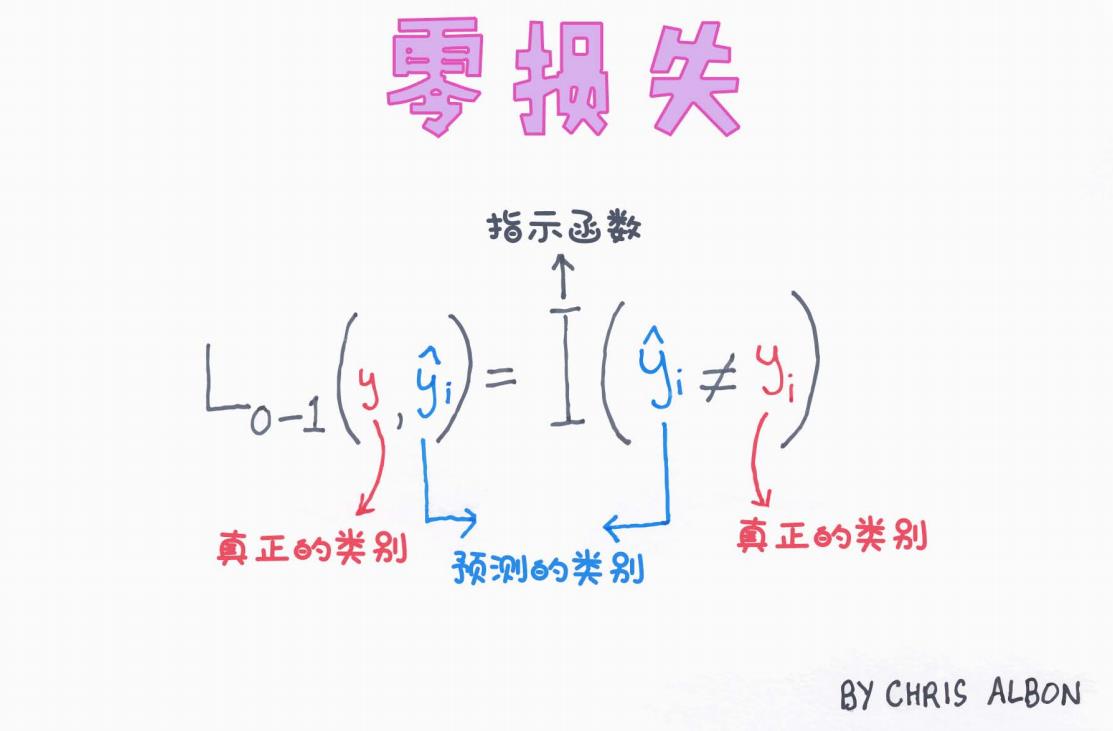
图中可以看到:
-
:真正的类别(红色标注)
-
:预测的类别(蓝色标注)
-
:当预测类别和真正类别不一致时,指示函数返回 1(即发生错误)。
通过这个简单的公式,我们能快速知道一个样本是否被分类器正确预测。
3. 零一损失在实际中的应用
虽然 0-1 损失函数非常直观,但在实际模型训练中,它通常不会直接作为优化目标,原因如下:
-
不可导性:由于 0-1 损失是离散的(只取 0 或 1),无法通过常规的梯度下降方法进行优化。
-
优化困难:在高维空间中直接最小化 0-1 损失是 NP-Hard 问题,非常难以计算。
因此,在训练模型时,通常采用替代性可导损失函数,比如:
-
逻辑回归使用的交叉熵损失(Cross Entropy Loss)
-
支持向量机(SVM)使用的铰链损失(Hinge Loss)
-
神经网络中也常用交叉熵或均方误差(MSE)
但在评估模型性能时,准确率(Accuracy)恰恰就是基于 0-1 损失计算的!
准确率公式:
也就是说,虽然训练过程中不用 0-1 损失,但它在测试和评估阶段非常重要!
小结
| 阶段 | 是否用 0-1 损失 |
|---|---|
| 模型训练 | ❌(通常不用) |
| 模型评估 | ✅(常用) |
4. 一个简单示例
假设我们有 5 个样本,真实类别和预测类别如下:
| 样本编号 | 真实类别 | 预测类别 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 0 | 1 |
| 3 | 1 | 1 |
| 4 | 0 | 0 |
| 5 | 1 | 0 |
对应的 0-1 损失:
-
样本 1:预测正确 → 损失 0
-
样本 2:预测错误 → 损失 1
-
样本 3:预测正确 → 损失 0
-
样本 4:预测正确 → 损失 0
-
样本 5:预测错误 → 损失 1
总损失:0 + 1 + 0 + 0 + 1 = 2
准确率:
即模型预测正确率为 60%。
5. 总结
-
零一损失函数用于判断预测是否正确。
-
训练过程中,通常不会直接优化 0-1 损失,但在评估时非常常用。
-
它为理解模型性能(特别是分类问题)提供了最基础、最直观的衡量标准。
掌握了零一损失,不仅能更好理解机器学习模型的性能评估,也为后续深入理解各种复杂损失函数(如交叉熵、KL散度等)打下坚实基础。
如果你觉得这篇文章对你有帮助,欢迎点赞、收藏、评论支持!
