当前位置：首页 > news >正文

leetcode - 双指针问题

news 2025/5/10 9:01:58

文章目录

前言

题1 移动零：

思路：

参考代码：

题2 复写零：

思考：

参考代码：

题3 快乐数：

思考：

参考代码：

题4 盛最多水的容器：

思考：

参考代码：

题5 有效三角形的个数：

思考：

参考代码：

题6 查找总价格为目标值的两个商品：

思考：

参考代码：

题7 三数之和：

思考：

参考代码：

题8 四数之和：

总结

前言

路漫漫其修远兮，吾将上下而求索；

题1 移动零：

283. 移动零 - 力扣（LeetCode）

提取题干意思：

思路：

数组划分类题型（数组分块）：给了我们一个数组，并且制定了一个规则，让我们在这个规则下将该数值划分为若干个区间

本题：

利用双指针，指针cur 从左往右遍历扫描数组，指针dest指向已处理区域非零元素最后一个位置，图解如下：

相当于指针cur、dest 将数据划分为了三段：[0,dest] 为非0的数据区域、[dest+1 , cur-1] 为0的数据区域，[cur,n-1] 为待扫描的数据区域（其中n表示数据个数）；

流程：eg. nums = [0,1,0,3,12]

思路总结：

注：双指针思想是快排中最核心的思想；虽可以解决快排问题，但是当数据量特别大的时候（例如相同的数据很多时），该方法的时间复杂度就接近N^2，因此快排不能解决比较恶心的数据（重复的数据多）；

参考代码：

    void moveZeroes(vector<int>& nums) {int n = nums.size();int cur = 0, dest = -1;while(cur<n){if(nums[cur]){++dest;swap(nums[dest] , nums[cur]);}cur++;}}

优化 - cur 的遍历可以使用范围for，代码如下：

    void moveZeroes(vector<int>& nums) {int cur = 0;for(auto& e:nums){if(e) {swap(e , nums[cur]);cur++;}}}

题2 复写零：

1089. 复写零 - 力扣（LeetCode）

提取题干意思：

思考：

我们先思考一下，异地操作（借助于其他空间）如何实现：

需要一个指针cur在旧数组上遍历，一个指针dest在新数组上遍历，当cur 遇到了0 就让dest 写两个0，cur 遇到非0，就让dest 写这个数据；图解如下：

Q1：是否可以从左往右直接使用双指针？

本题不行，因为遇见0要在原数组上写两个0，会覆盖掉后面的数据；但是如果是删除值为val 的题，就可以这么做；

Q2：既然从左往右不可行，那么从右往左是否可行呢？

从右往左的话，就需要找到cur 最后一个所要“复写”的位置，如何找？

这与整个数组中0的个数有关系，可以先利用双指针（cur,dest）从左往右遍历（cur遇到0,dest走两步，非0dest走一步;当cur 走到最后一个数据或者dest 走到最后一个的时候，cur 指向的位置就是最后一个所要“复写”的位置），找到最后一个所要复写的位置，然后此时cur 、dest 的位置就是从右往左复写数据时的位置，思路图如下：

注：dest 指向有效数据的结尾，初始化为-1；cur 初始化为0；

但是，如果当cur 指向0，而dest 往后走两步可能就会越界，如果dest 越界了；而此时cur 、dest 的位置会作为从右往左复写数据时的位置，但是dest 已经越界了，故而这是有问题的；

解决方法：在找位置结束后判断dest 是否合法（dest小于等于n-1就是合法的范围，但是dest 如果越界是一定等于n）;如果合法什么都不做，如果不合法，dest = n-1 ，cur--;arr[n-1] = 0，如下图：

即，在找最后一个所要复写的位置的时候，有三种情况回导致循环结束：

参考代码：

    void duplicateZeros(vector<int>& arr){int n = arr.size();int cur = 0, dest = -1;//先从左往右遍历，找到cur 指向的最后一个数据while(cur<n){if(arr[cur]==0) dest+=2;else ++dest;//在此过程中dest 可能会越界//在cur 自增前判断dest 是否越界if(dest >= n-1) break;//因为n-1 是最后一个有效位置 cur++;}//边界情况处理，dest 越界了一定是为nif(dest==n){arr[n-1] = 0;dest-=2;--cur;}//从先有的cur dest 的位置进行复写操作while(cur>=0){if(arr[cur]==0){arr[dest--] = 0;arr[dest--] = 0;}else{arr[dest--] = arr[cur];}cur--;}}

题3 快乐数：

202. 快乐数 - 力扣（LeetCode）

提取题干意思：

思考：

根据例子，画图思考：eg. 19 、2

对于19，最后得到是1在循环，故而返回的是true;对于2，最后得到的不是1的循环，所以返回false;

要么最后是1，陷入1的循环；要么不是1但是最后陷入一个循环之中

图解是否感觉有点熟悉？是不是有一点像链表，如果转换成链表，就是判断这链表环中的值即可（因为一旦有1，就一定是1为一个单独的循环);而在链表 - 判断链表是否有环，是用快慢双指针来解决；

可以将本题抽象成链表，一个数变化成一个数可以抽象成这些数串联了起来；并且在本题中不用判断是否有环，只需要判断环中的值便可；

需要注意的是，slow 初始化为第一个数据的位置，fast 初始化为slow 的下一个位置；

只需要判断这两个值相遇的值是不是1即可，是1就返回true ,不是1则返回false;

在这个过程中是一定成环的；

注：

1、在带环的链表中，快慢双指针一定会相遇，并且一定会在环中相遇；

2、本题中虽然不像链表中是一个一个结点，只是一个一个的数，我们也可以让数来充当“指针”；不要被指针这个词限制了思维，此处所讲的指针并不是真正的指针，而是在数组中使用双指针的时候可以用数组下标来充当指针，因此“双指针”只是一种思想；

本题题干中：，所以就一定回成环，但是如果题干如果没有给这个提示呢？

那么分析地时候，就会分析出第三种情况：变下去不会成环；存在不成环的情况吗？如果题干没有这个提示，我们又该如何解决？

证明：为什么在变化的过程中一定会有环？

我们先来了解一个原理：鸽巢原理（抽屉原理）

注：我们的证明会用到鸽巢原理

取 9999999999 是因为它是 2.1*10^9 同样位数中的最大的数，可以靠它看一下范围；

对于 9999999999 来说，经过“操作”它每一位的和为 9^2*10 = 810，也就是9999999999经过“操作”之后所能变成的最大的数，即对于 9999999999 来说有810 个巢，而 2.1*10^9 小于9999999999，那么 2.1*10^9 经过操作之后的结果一定小于等于9999999999 经过“操作”之后的结果810，即2.1*10^9 的巢得个数一定小于等于810并且大于等于1；

2.1*10^9 的巢得个数：[1，810]

那么一个数如果进行了“操作”大于810 次（操作次数是无限的），必定就会循环，即该数一定成环；（即将大于810 的鸽子放到810 个巢里面，必定有一个巢中的鸽子数量大于1）就可以证明没有第三种情况：变下去不会成环；

经过上述证明，数据在变化的过程中一定会成环；

参考代码：

    //获取一个数的每一个位置上的平方和int getbit(int n){int tmp = n, sum  = 0;while(tmp){int t  = tmp%10;//每一位sum += t*t;//平方和tmp/=10;//迭代}return sum;}bool isHappy(int n) {//通过鸽巢原理可以证明一定成环，所以可以利用快慢双指针来解决这个问题//注意slow 与 fast 的初始化！int slow = n , fast = getbit(n);//当slow 与 fast 相遇的时候，一定在环中相遇，此时只需要判断相遇的值便可while(slow!=fast){//slow 一次走一步//fast 一次走两部slow = getbit(slow);fast = getbit(fast);fast = getbit(fast);}if(slow == 1) return true;else return false;}

可以优化一下上面的参考代码，优化代码如下：

    //获取一个数的每一个位置上的平方和int getbit(int n){int tmp = n, sum  = 0;while(tmp){int t  = tmp%10;//每一位sum += t*t;//平方和tmp/=10;//迭代}return sum;}bool isHappy(int n) {//通过鸽巢原理可以证明一定成环，所以可以利用快慢双指针来解决这个问题//注意slow 与 fast 的初始化！int slow = n , fast = getbit(n);//当slow 与 fast 相遇的时候，一定在环中相遇，此时只需要判断相遇的值便可while(slow!=fast){//slow 一次走一步//fast 一次走两部slow = getbit(slow);fast = getbit(getbit(fast));}return slow==1;}

题4 盛最多水的容器：

11. 盛最多水的容器 - 力扣（LeetCode）

数据范围：

例子：

思考：

解法一：暴力解法

将所有两两组合的情况均列举出来，找到其中的最大值即可；此处的数据量约有 10万，使用暴力解法的时间复杂度为 O(N^2) ,一定会超时的，不过此处我们还是尝试一下用暴力解法是否能过：

测试用例能通过，但是提交之后：

解法二：利用单调性使用双指针

为什么会想到用单调性？

如果想要找到两数相乘再乘以其底面积的最大值，一定是从左边区域中找一个最大的乘以右边区域中最大的数；使用双指针一个从左边开始，一个从右边开始，谁小谁就往自己所在的方向移动；而如果有一个木桶，它的板高度不一样，它所能所能存多少水是由最短的板决定的，所以我们该用短板才会有效果，而桶底也是变化的，所以还需要一个变量来记录体积；

例子：

思路总结：定义两个指针left right ,根据这两个指针指向的数据，记录计算出来的体积，谁小谁移动，循环下去更新得到的最大值；循环条件：left<right;

参考代码：

    int maxArea(vector<int>& height) {//体积由短板决定int left = 0 , right = height.size()-1 ,ret = INT_MIN;while(left<right){//体积 = 短板长度*底面积int v = (height[left]<height[right]?height[left] : height[right]) * (right-left);ret = max(ret , v);//谁小谁移动if(height[left]>height[right]) right--;else left++;}return ret;}

题5 有效三角形的个数：

611. 有效三角形的个数 - 力扣（LeetCode）

题干：

数据范围：

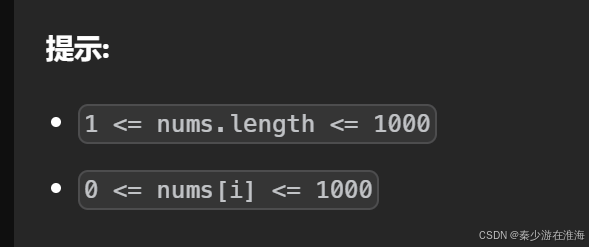
例子：

思考：

本题无非就是枚举出所有的三个数，然后判断这三个数能否组成三角形；

Q：如何判断三个数能否构成三角形？

首先会想到的是“两边之和大于第三边”，让三个数两两组合然后与第三个数比较，看是否符合就行，但是这种判断方式需要判断三次，效率上有点低，有没有高效点的判断方法？

第二种判断方法：让较小两边相加与最长边比较，如果是大于则就可以构成三角形；

因为最长边一定是大于较小边的（另外两个情况），所以只要保证让较小两边相加大于最长边便可，图解如下：

而对于枚举，首先我们一定会想到的是暴力解法，利用循环枚举出所有的情况，然后判断，这种方法的时间复杂度为O(N^3)，先试一下暴力解法能否通过：

使用暴力解法，测试用例可以通过，但是提交：

不能使用暴力解法解决，还能怎么做？

我们前面曾说，判断两个数能够构成三角形，如果得到了这三个数的大小关系，可以拿较小的两个数与最大的那一个数进行比较，不可能每次拿到三个数就先比较大小吧？暴力枚举依然是个痛处，既然在比较的时候就要知道数据的大小关系，那么我们可以先对数据进行排序，利用数据的单调性以及三指针；

当 b + c > a 时（即 b 和 c 指向的数据之和大于 a 指向的数据），这三个数必定可以构成三角形。此时，区间 [b+1, c-1] 内的数据均大于 b，且与 c 相加后仍满足大于 a 的条件，那么就有（c-1-b+1）个数符合要求，利用变量记录；然后 c 减 1，继续在下一个区间进行判断
当 b + c < a 时（即 b 和 c 指向的数据之和小于 a 指向的数据），这三个数无法构成三角形。此时，区间 [b+1, c-1] 内的数据均小于 c 指向的数据，不符合要求，无需记录，直接让 b 加 1，继续在下一个区间中寻找符合条件的组合。

最大的数a 从右往左遍历，b初始化为0，c初始化为a-1;

这就是解法二：利用单调性，使用双指针方法来解决问题，稍微总结一下：

1、先固定最大的数
2、在最大的数的左区间中，使用双指针算法，快速统计出符合要求的三元组的个数；

举个例子：

参考代码：

    int triangleNumber(vector<int>& nums) {//先对数据进行排序处理sort(nums.begin() , nums.end());int n = nums.size();int a = n-1 , ret = 0;//指向最大的指针for( ; a>=2;a--){int b = 0, c = a-1;//让较小的两个while(b<c){if(nums[b]+nums[c]>nums[a]) //b->[b,c-1] 区间中的数据均合理 {ret+=(c-1-b+1);c--;//去下一个区间}else //不符合要求，那么c->[b+1,c] 中的均不符合{b++;}}}return ret;}

题6 查找总价格为目标值的两个商品：

LCR 179. 查找总价格为目标值的两个商品 - 力扣（LeetCode）

题目：

数据范围：

例子：

思考：

方法一：暴力解法

将所有的两个数的组合列举出来然后进行比较

伪代码：

可以试一下用暴力解法能否通过算法：

提交：

暴力解法不行；

方法二：题干中说过price 数组中的数据为升序，我们可以利用好单调性；最先想到的可能是二分算法，但是此处不推荐使用二分，我们可以利用单调性+双指针来解决；

设置两个指针：left 与right , 让left 指向最左的数据，让right 指向最大的数据，如果left + right 的结果大于 target ，那么right--;如果left + right 的结果小于target 那么left++;图解如下：

总结算法逻辑：

参考代码：

    vector<int> twoSum(vector<int>& price, int target){//利用数据的单调性+双指针int n = price.size();int left = 0, right = n-1;while(left < right){if(price[left]+price[right] > target) right--;else if(price[left]+price[right] < target) left++;else return {price[left] , price[right]};}//没有找到，返回空return{};}

题7 三数之和：

15. 三数之和 - 力扣（LeetCode）

题干如下：

数据范围：

例子：

思考：

即在数组中找到三个不重复的数据让其相加为0；

根据前面做过的题的经验，我们可以先将数据进行排序处理；

Q：如何让找到的三个数据不重复呢？

可以首先将nums 中的数据进行去重处理，利用set就可以了;

解法一：暴力解法：排序 + 暴力枚举 + 利用set 进行去重

此处就不验证暴力解法是否能通过了，数据量有10万，时间复杂度为O(N^3) 的算法一定会超时；

解法二：排序 + 固定一个数a ，利用双指针找到何为-a 的两个值

这样的话，”利用双指针找到何为-a 的两个值“ 的思路就与题6中的思路非常像；

Q：那么去重呢？

笔试中可以利用容器set进行去重，但是在面试中不推荐这么做；本题，我们开始就对数据进行了排序处理，那么相同的数据就已经放在了一起；当我们找到了一个结果的时候left 和 right 该如何移动？left 和 right 要跳过与当前所指数相同的重复的数据，继续缩小空间继续查找，同样的，我们固定的数a 也需要进行去重处理，当使用完一轮双指针算法之后，a 也需要跳过重复的数据；

要做到不重不漏；

参考代码：

    vector<vector<int>> threeSum(vector<int>& nums) {//首先先对数组进行排序sort(nums.begin(), nums.end());int n = nums.size();vector<vector<int>> ret;for(int i = 0 ;i< n; ){int left = i+1, right = n-1;while(left < right){int target = -nums[i];int sum = nums[left] + nums[right];if(sum > target) right--;else if(sum < target) left++;else{ret.push_back({nums[i], nums[left] , nums[right]});left ++ ,right--;//去重while( left < right && nums[left] == nums[left-1]) left++;while( left < right && nums[right] == nums[right+1]) right--;}}//一轮双指针结束之后，还要对固定的数进行去重处理++i;while(i<n && nums[i] == nums[i-1]) ++i;}return ret;}

题8 四数之和：

18. 四数之和 - 力扣（LeetCode）

题干：

数据范围：

例子：

思考：

本题的解题思路非常浅显：找到4个数 + 判断是否相加为target

找数就有讲究了，要么暴力枚举，要么使用比较巧妙的方法，同样的，本题要求不包含重复的数据，我们可以考虑使用set 去重；

通过数据范围就知道，我们要使用long long ；

解法一：排序 + 暴力解法 + 利用set去重

本题的数据量很大，并且要暴力枚举出4个数，实践复杂度非常高，一定会超时，此处就不演示了；

解法二：排序 + 双指针

可以参考上题三数之和的思路；

首先是将数据进行排序，利用数据有序的特点可以提高效率；然后是固定一个数，再固定一个数，剩下两个数利用双指针；可以理解为，我们先固定一个数a，那么题目就变成在除了固定的的这个数中找和为（target-a）的三个数：

最后需要做到“不重不漏”，本题会设置三个循环，两个循环用来固定两个数，一个循环适用于双指针，这三个循环都需要关注去重处理（如果不用set 去重的话）；而关于不漏，在双指针查找的过程中，我们要在left 和 right 中找到和为目标值时，不能直接结束当前的双指针查找循环，而是要left++,right-- 且left<right ，继续查找下去；

初次尝试：；

计算目标值的时候，记得用long long!

参考代码：

    vector<vector<int>> fourSum(vector<int>& nums, int target) {//首先对数据进行排序sort(nums.begin() , nums.end());int n = nums.size();vector<vector<int>> ret;//固定数afor(int i = 0; i<n; ){//固定数bfor(int j = i+1;j<n; ){long long t = ( long long)target - nums[i] -nums[j];//双指针查找int left = j+1,right = n-1;while(left < right){int sum = nums[left] + nums[right];if(sum > t) right--;else if(sum < t) left++;else{//将数据放入数组中ret.push_back({nums[i] , nums[j] , nums[left] , nums[right]});//去重left++,right--;while(left < right && nums[left] == nums[left-1]) left++;while(left < right && nums[right] == nums[right+1]) right--;}}//固定的第二个数的去重++j;while(j<n && nums[j] == nums[j-1])j++;}//固定的第一个数的去重++i;while(i<n && nums[i] == nums[i-1])i++;}return ret;}