一文详解极大似然估计,从极大似然估计的角度理解线性回归
1. 极大似然估计的概念
1.1 似然与概率
似然估计与我们熟知的概率问题是一个相反过程,概率是指当我们知道一些条件或者参数,来预测某件事情发生的概率,例如,当我们知道了天气,温度等来预测晾衣服的概率。
再例如抛硬币,我们已知的条件是硬币材质均匀,大小均匀,因此可以预测正面朝上的概率是0.5,反面朝上的概率是0.5
而似然是一个相反的过程,还是抛硬币的例子,现在我们假设抛10000次硬币,其中8000次人像朝上,2000次数字朝上,基于这个结果,我们推断,硬币可能构造特殊。进而推测硬币的参数,人像概率是0.8,数字概率是0.2。这种根据结果来判断事物本身性质的过程就是似然。

我们假设是环境对应的参数,x表示事件发生的结果,那么概率可以表示为
,即环境参数为
的条件下,事件x发生的概率。
而似然是即在已知事件结果x的前提下,去推断
。
其中p是关于x的函数,L是关于的函数
 1.2 极大似然估计
1.2 极大似然估计
极大似然估计也叫最大似然估计,即根据已知的结果来推测最具可能让这个结果发生的参数设置,这是一个已知观测数据来推断模型参数的过程。
依然是抛硬币的例子,如下图所示:

此时抛硬币事件的似然函数为,求使得该函数取得最大值的
,就是在求极大似然估计了。当
等于0.7的时候似然函数取得最大值。


2. 从极大似然估计的角度理解线性回归
2.1 线性回归问题
在线性回归中一般假设特征x和目标值y的关系是线性的
比如对于一维的数据分布,可以利用线性回归来描述这组数据,直接建立函数,,其中
是偏置项,一般将其缩并在
中,一起组成参数向量。完成建模后有无数种参数可以选择,有无穷多的参数都可以穿过数据点,看起来都还不错,但是哪一组是最好的呢?

这也是机器学习最核心的问题,此时我们应该找一个损失函数,这个损失函数描述了最好的参数值应该满足什么条件,从常识来看数据与函数对应点的欧氏距离可以作为有效指标,因为距离越近,误差越小,说明预测的越准,所以只需要计算对应点之间距离的平方,然后把他们全部加起来,同时还是连续光滑的就可以作为一个损失函数。

呢么我们要找什么参数呢?

这就是最小二乘估计
2.2 高斯分布
高斯分布又叫正态分布对所有形如的分布,同城为高斯分布,也叫正态分布,
当均值为0,方差为1时叫做标准正态分布
当均值变化时,分布会在坐标轴上平移,方差控制分布的峰度,当方差变大时峰值会降低,分布相对来讲比较平缓,当方差变小时,峰值会变高,分布比较集中。
我们可以从高斯分布中采样数据,这些数据都是独立同分布的,高斯分布的定义域是负无穷到正无穷,每一个采样到的数据在任何一个其他的高斯分布中都可以采样到,但是如果现在有一组采样的数据,我们怎么判断他最应该是哪个高斯分布中采样出来的呢?

其实每一个数据被采样的概率都可以写成一个条件概率的形式,表示从参数和
的高斯分布中被采样的可能性大小,由于他们是同分布的所以每一个条件概率中的参数
和
是一样的,又由于他们是独立的,因此他们同时出现的的概率也就是联合概率,体现为概率的连乘。那么我们的任务就很明确了:找到一个高斯分布,让这组数据出现的可能性最大,也就是使得联合概率最大


由于多个小于1的数字连乘会变得非常小,以至于最后体现在模型中可能会引起梯度消失,因此我们一般引入log将其转变为加法操作:

以上就是极大似然估计的基本思想
2.3 从极大似然估计理解线性回归问题
还是之前那个线性回归的图,只不过我们这次不把x, y一起来看,而是拆开来看,将y理解为一个从正态分布中采样到的值,wxi相当于是前置条件,合起来就是在的前提下,采样到y的概率,我们的目的是要让所有的点的概率乘积最大。图中所示是y在他自己的标准正态分布中采样的示意图

关于这部分的详细理解见下图:
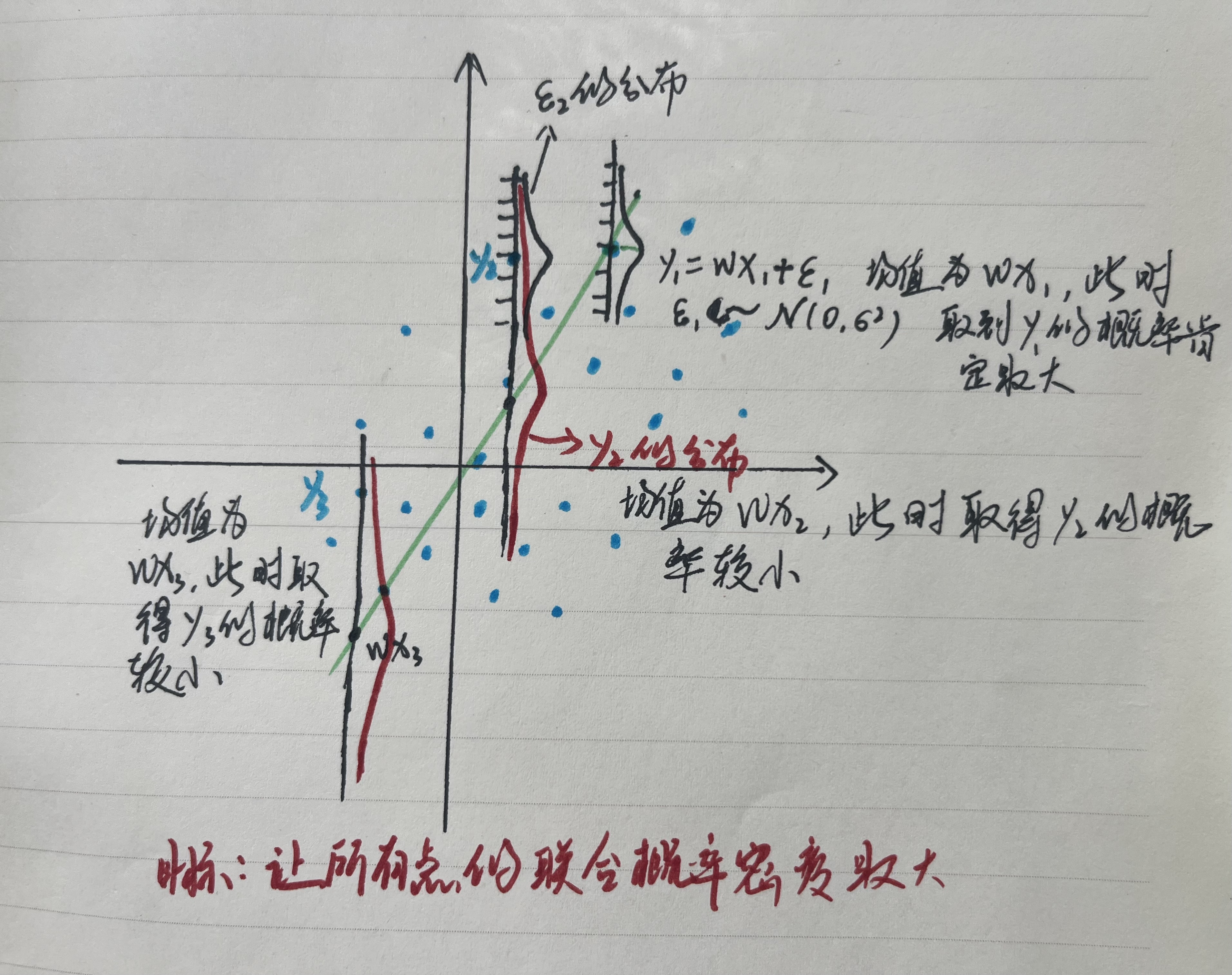
这所有的数据都遵循同一个条件分布(虽然均值不同,但他们来自同一个参数化模型族),所以可以统一计算参数,且数据点相互独立。

将概率密度函数代入:


其中是噪声的参数,与模型无关,因此可以直接剔除,那么整个式子就变成了:



最终我们重新得到了最小二乘估计。因此最小二乘估计只是极大似然估计在高斯分布下的一种特殊形式。如果我们假设其他分布,比如伯努利分布,极大似然估计的结果就是逻辑回归;如果假设多项分布,那么我们就会得到softmax回归。
